变换自动编码器（Transforming Auto-Encoders）翻译

本文是对于Geoffrey E. Hinton, Alex Krizhevsky, and Sida D. Wang在2011年发表的论文《Transforming Auto-Encoders》的翻译。

变换自动编码器（Transforming Auto-Encoders）

摘要：用于识别形状（shapes）的人工神经网络通常使用学习特征检测器（learned feature detectors）的一层或者多层产生标量输出。相比之下，计算机视觉领域使用复杂的、手工设计的特征，比如SIFT[6]，产生一个完整的输出向量，其包括特征的姿态（pose）的显式（explicit）表示。我们解释了如何使用神经网络学习特征，这些特征输出实例化参数的完整向量，我们认为该方法对于处理位置、方向、尺度和光照变化比在神经网络领域的现有方法更有前景。它也比目前用于计算机视觉的人工设计的特性更有前景，因为它提供了一个让特征适应领域（domain）的有效的方法。

关键词：不变性（Invariance），自动编码器（auto-encoder），形状表示（shape representation）。

1 引言

目前，图像中目标识别方法的结果不是很好，在智能上，也无法令人满意。一些最好的计算机视觉系统使用梯度导向的直方图作为“视觉词”，并使用一个粗略的空间金字塔对于这些元素的空间分布建模。这种方法能够在不知道确切位置的情况下正确识别目标，可以用于诊断人类的脑损伤。最好的人工神经网络使用手工编码的权重共享方案来减少自由参数的数量，他们通过对相同的核的变换复制的局部池（local pools）的激活进行下采样，实现了局部平移的不变性（local translational invariance）。毕竟，这种处理由于视角变换而引起的图像变化的方法要比没有方法好很多，但是，该方法显然不能处理的是识别任务，比如面部身份识别，其需要如一个鼻子和一个嘴这样的高层部分之间精确的空间关系的知识。在卷积网络中进行了多次下采样后，它们的姿态中，高层特征就有了很大的不确定性。通常认为它是一种理想的属性，因为 姿势 在有限范围内有不变性，但是，使得它不可能计算精确的空间关系。

本文认为，卷积神经网络在他们尝试去实现什么的问题上被误导了。我们不是以“神经元（neurons）”的激活中的视角不变性为目标，这些“神经元”用一个单一的标量输出来总结复制得到的重复的特征检测器的一个局部池的激活，而是使用局部“胶囊（capsules）”，这些“胶囊”可以对输入完成一些非常复杂的内部计算，之后将这些计算结果封装成一个具有高度信的信息输出的小的向量。在一个有限的观察条件（viewing conditions）和形变的领域，每个胶囊（capsule）学习识别一个隐式定义的视觉实体，它的输出是实体出现在有限的领域内的概率，也是一些可能包括视觉实体正确的姿态、光照和形变“实例化参数”，这与该实体的隐式定义的标准版本有关。当胶囊正常工作时，视觉实体出现的概率是局部不变的，即在胶囊覆盖的有限的领域内，概率不会随着实体在可能的表观流形（the manifold of possible appearances）上的移动而改变。然而，实例化参数是随着观察条件的变化而同时变化的（equivariant），实体在表观流形（appearance manifold）上移动时，实例化参数也会有相应数量的改变，因为它们表示了在表观流形上的实体的内在坐标。

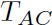输出显式的（explicit）实例化参数的胶囊的一个主要优势是它们提供了一种通过识别它们的各个部分从而来识别整体的简单方法。如果一个胶囊可以用一个向量学习输出它的视觉实体的姿态，这个向量是一个与用于计算机图形学中的姿态的自然地表示线性相关的，对于视觉实体是否可以用两个有着正确的空间关系来激活更高层胶囊C的激活胶囊A和B表示，这里有一个简单的和高度可选择的测试。假设用一个矩阵表示胶囊A的姿态输出，其指定了A的标准视觉实体和通过胶囊A建立的实体的真实的实例化间的坐标变换。如果我们用一个部分-整体的坐标变换乘以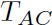，是A的标准视觉实体和C的标准视觉实体的关系，我们就会得到对于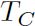的一个预测。相似的，我们可以用和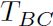获得另一个预测。如果这些预测是一个很好的匹配，胶囊A和B建立的实例化是在正确的空间关系中激活胶囊C，预测的平均告诉我们，用C表示的更大视觉实体如何变换成与C的标准视觉实体相关。例如，在正确的空间关系中，A代表一张嘴，B代表一个鼻子，它们每个都可以对脸的姿态做一个预测。如果这些预测是一致的，那么嘴巴和鼻子一定是在正确的空间关系中形成的一张脸。这种进行形状识别的方法的一个有趣的特性是，部分-整体关系的知识是视角-不变（viewpoint-invariant）的，并且是用权重矩阵表示的，然而，目前观察到的目标和目标的部分的实例化参数的知识是视角-同变的（viewpoint-equivariant），并且是用神经的激活来表示[12]。

为了开始得到这样一个部分-整体的层次结构，层次结构中最低层次部分的“胶囊”需要从像素强度中去提取显式的姿态参数。该论文表明，如果神经网络有直接的、非视觉的使用这些变换，那么这些胶囊可以很容易的从变换图像对中学习。例如，在人类中，眼睛的飞快扫视会引起视网膜图像的一个清晰的转化，皮层对于关于眼镜移动的信息有着非视觉的获取。

2 学习胶囊的第一层

一旦像素强度转换为一系列激活的、第一层胶囊的输出，每一个胶囊都会产生一个对于它们的视觉实体的姿态的显式表示，可见通过使用激活的、较低层胶囊预测姿态的一致性如何识别更大、更复杂的视觉实体是比较容易的。但是，第一层胶囊从何而来呢？一个人工神经网络如何学会将像素强度的语言转换为姿态参数的语言？这就是本文所解决的问题，结果发现，有一个非常简单的答案，我们称之为“变换自动编码器（transforming auto-encoder）”。我们用简单的二维图像和胶囊来解释该想法，它的唯一输出是x和y的位置。稍后，我们会将其推广到更加复杂的姿态。

考虑图1所示的前馈神经网络。网络是确定的，一旦开始对网络进行学习，网络的输入就是一幅图像和预期的位移和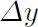，输出是位移后的图像。每个胶囊都有它自己的逻辑“识别单元（recognition units）”，逻辑识别单元作为隐藏层来计算x、y和p三个数，这是胶囊将发送到视觉系统的更高层的输出。p是胶囊的视觉实体在输入图像中存在的概率。胶囊也有自己的“生成单元（generation units）”，用于计算胶囊对于变换后的图像的贡献（contribution）。生成单元的输入是x+和y+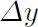，胶囊的生成单元对输出图像所做的贡献要乘以p，所以未激活的胶囊没有作用。

图1. 对于平移建模的变换自动编码器的三个胶囊。图中的每个胶囊有三个识

别单元和四个生成单元。通过反向传播实际输出的和目标输出间的差异来学习连接权重。

为了用变换自动编码器产生正确的输出图像，用每个对应于它的视觉实体的真实x和y位置的激活胶囊来计算x和y位的值是至关重要的，我们不需要提前知道这个视觉实体或者它的坐标系的原点。

作为一种变换自动编码器效果的简单说明，我们训练了一个有30个胶囊的网络，每个胶囊有10个识别单元和20个生成单元。每个胶囊都可以看到一幅MNIST数字图像的全部。输入图像和输出图像在x和y位方向上随机移动-2、-1、0、+1或+2个像素，变换自动编码器得到的结果和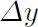作为附加的输入。图2表明胶囊用高度局部化的投影区域学习生成单元。识别单元的感受野（receptive fields）是更嘈杂的和稍微更少的局部化。

图2. 左：一幅散点图，纵轴表示每幅数字图像的其中一个胶囊的x输出，

横轴是表示如果一幅图像在x方向上移动+3或-3个像素时的同一个胶囊的x输出。

如果原始图像已经接近胶囊可以表示的x位置的极限，在该方向上的进一步移动会导致胶囊产生错误的结果，

但是，如果对于它能力领域外的数据，胶囊设置它的概率为0，这就不重要了。

右：其中9个胶囊体的20个生成单元的10个权重。

2.1 更复杂的二维变换

如果给每个胶囊9个实值输出，作为一个3 × 3的矩阵A，可以训练一个变换自动编码器来预测一个全部的二维仿射变换（full 2-D affine transformation）（平移、旋转、缩放和裁剪），对胶囊A的输出应用一个已知变换矩阵T来获得矩阵TA。之后，当预测目标输出图像时，用TA的元素作为生成单元的输入。

图3. 上面：使用一个由25个胶囊组成的变换自动编码器进行全仿射变换（full 

affine transformations），每个胶囊有40个识别单元和40个生成单元。

第一行是输入图像；中间行是输出图像；第三行是正确变换的输出图像。

下面：这个变换自动编码器的前7个胶囊的前20个生成单元的输出权重。

2.2 在3维视角中建模的变化

用矩阵乘法对视角的影响进行建模的一个主要的潜在优势是它处理3维更加容易。我们初步实验（见图4）用计算机图形学产生不同视角的不同类型的立体图像。变换自动编码器由900个胶囊组成，每个都有两层（先是32个，后是64个）修正线性识别单元[8]。胶囊有11x11像素的感受野，这些感受野被安排在96x96图像上的一个30x30的网格上，相邻胶囊间的步长是3个像素。没有共享的权重。每个胶囊都是产生于它的64个识别单元的层，它的被用来检测特征的3维方向的一个3x3矩阵表示，也是所呈现出的它的隐式定义特征的概率。之后，这个3x3矩阵乘以一个源图像（source images）和目标图像（target images）间真实的变换矩阵，结果被送到胶囊的128个生成的修正线性单元。生成单元激活乘以胶囊的“特征出现（feature presence）”概率，结果用来增加重建图像的中心在胶囊的11x11感受野的中心上的一个22x22块（patch）的强度。由于这些数据都是由立体的图相对（stereo pairs of images）组成，每个胶囊要考虑两个立体对的成员中一个11x11块，同时在两个成员中重建一个22x22块。

图4. 左：训练数据的输入、输出和目标立体对。

右：在训练中未见到的小车模型的输入、输出和目标立体对。

3 讨论

使用多个实值（real-values）是表示姿态信息的自然方式，它比使用粗糙的编码更有效[3]，但是，它是有代价的：与价值捆绑在一起的唯一的事情是它们是同一胶囊的姿态输出的事实，所以，在同一时间，用一个胶囊表示它视觉实体的多个实例是不可能的。看起来，在相同的有限域中，不能允许同一视觉实体的多个、同时的实例是一个严重的弱点，的确如此。它可以通过在姿态空间的一个非常有限的区域上对每个最低层胶囊进行操作来得到改善，并仅允许更复杂的密度分布更低的视觉实体的更大区域。但是无论该区域多小，都有可能通过同一区域的细微的不同姿态的同一视觉实体的两个实例混淆系统。“拥挤”[9]现象表明这种类型的混淆可能发生在人类视觉中。

单从机器学习的角度来看，为网络提供一个额外的指定图像变换方式的输入可能显得多余，因为这一信息原则上可以从两个图像中计算得到[7]。然而，这些信息常常是直接可以使用的，从而使学习变得更简单。指定图像的一个全局变换比显式的指定特征的姿态更简单，因为它不需要做到什么视觉实体应该被每个胶囊提取，或者在表示视觉实体姿态时，应该使用什么样的内在坐标系，就可以完成。

在一个卷积神经网络中，一个胶囊与单元的一个局部池有一些相似之处，因为许多识别单元在稍微不同的位置有着非常相似的感受野。然而，有一个非常重要的区别，所有识别单元的输出的方式是封装到更高层来使用。在卷积池中，下采样后的组合输出通常是池中最大激活单元的标量激活[11]。即使这个单元的位置对于无监督学习所需创建重建时使用，它也不会被更高层使用[5]，因为卷积网络的目的是活动的平移不变性。而且，即使用于重建的位置被传递到更高层，它也只会有整数值的坐标。一个胶囊可以更好地利用识别单元的输出来计算精确的位置坐标，精确到一个像素的一小部分。在这一方面，它类似于一个可操作的滤波器[2]，但是不像大多数可以操作的滤波器那样，它学习识别单元的感受野来优化计算得到的坐标的准确度，它也用来学习什么视觉实体来表示。复制完全相同的权重核对于在有限域上提取一个视觉实体的姿态是不佳的，特别是如果复制必须覆盖尺度、方向和位置。

变换自动编码器与卡尔曼滤波器也有一种有趣的关系。将卡尔曼滤波器应用到观测到的非线性函数的动态（dynamics）数据的最常用的方法是“扩展（extended）”卡尔曼滤波器，它将有关于当前工作点的动态线性化。这通常很有效，但也明显是一种违规行为。如果我们将输入和期望输出视为暂时邻接，则变换自动编码器是使用线性动态模型的一个更加有原则的方法。识别单元学将输入映射到一种表示，其中的动态实际上是线性的。当这些胶囊的姿被态线性变换后，生成单元映射回观测域。通过测量观测域中的错误，我们避免了计算决定因素的需求，即追踪在两个域间移动的错误被压缩或扩展的程度的。

如果我们消除了给与变换自动编码器变换的直接知识的额外输入，我们可以将相邻时间帧之间的小变换作为零均值高斯噪声来建模。这使得变换自动编码器变为一种不是很好的学习方法，这种方法只能找到那些连续图像间无明显变化的缓慢的特征。

在[1]中提出的模型用一个非常不同的学习过程学习一个与变换自动编码器相似的表示。胶囊计算的局部不变概率类似于它们的复杂细胞的输出，而同变的实例化参数类似于它们的简单细胞的输出。它们在不使用变换知识的情况下学习，但是它们只学习图像的线性函数实例化参数。

一个变换自动编码器可以得到一个胶囊的输出来表示一幅我们用已知方式操作的图像的任何属性，例如，很容易放大所有的像素强度。如果一个第一层胶囊输出一个数量，这个数量是首先乘以亮度尺度因子，然后在预测经过亮度变换的输出时，对其生成单元的输出进行缩放，这一数字将学会表示亮度，并将允许胶囊解开来自于实例的亮度的它的视觉实体的一个实例的概率。如果可以控制一个场景的照明方向的变化，一个胶囊可以输出两个表示该方向的数字，但是，只是在视觉实体允许从识别单元的激活中提取光照方向足够复杂的时候。