numpy【极简】RNN
文章目录
- 序言
- 极简代码
- 和[普通神经网络]的差异
- 训练过程打印
序言
原文出处:http://iamtrask.github.io/2015/11/15/anyone-can-code-lstm/
示例为RNN实现二进制加法,用来帮助理解RNN
可以先看原文(RNN原理和源代码),再看本文
源代码比较冗余,下面是精简后的代码
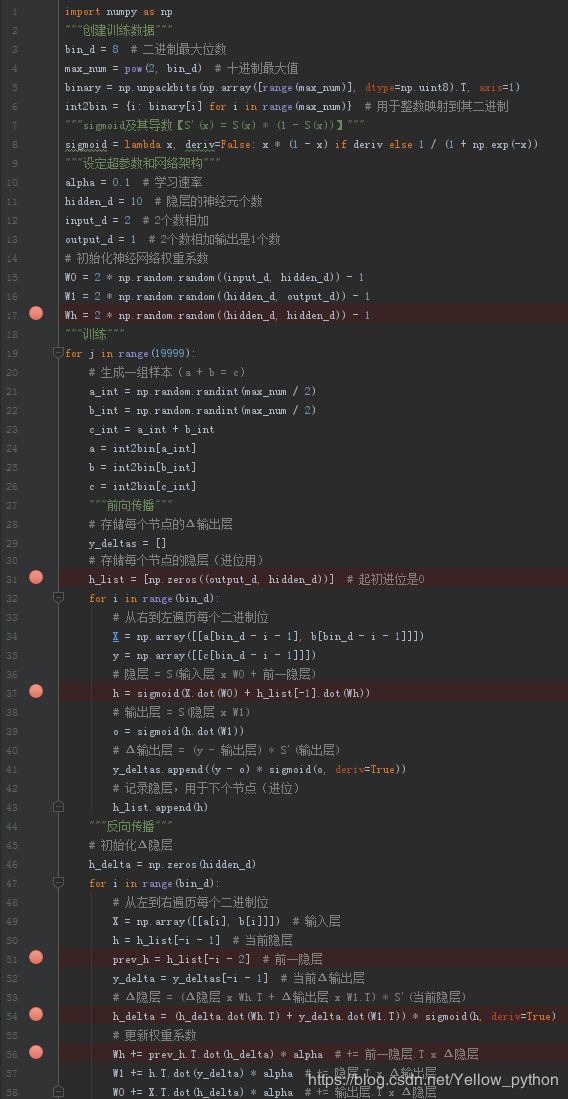
极简代码
import numpy as np
"""创建训练数据"""
bin_d = 8 # 二进制最大位数
max_num = pow(2, bin_d) # 十进制最大值
binary = np.unpackbits(np.array([range(max_num)], dtype=np.uint8).T, axis=1)
int2bin = {i: binary[i] for i in range(max_num)} # 用于整数映射到其二进制
"""sigmoid及其导数【S'(x) = S(x) * (1 - S(x))】"""
sigmoid = lambda x, deriv=False: x * (1 - x) if deriv else 1 / (1 + np.exp(-x))
"""设定超参数和网络架构"""
alpha = 0.1 # 学习速率
hidden_d = 10 # 隐层的神经元个数
input_d = 2 # 2个数相加
output_d = 1 # 2个数相加输出是1个数
# 初始化神经网络权重系数
W0 = 2 * np.random.random((input_d, hidden_d)) - 1
W1 = 2 * np.random.random((hidden_d, output_d)) - 1
Wh = 2 * np.random.random((hidden_d, hidden_d)) - 1
"""训练"""
for j in range(19999):
# 生成一组样本(a + b = c)
a_int = np.random.randint(max_num / 2)
b_int = np.random.randint(max_num / 2)
c_int = a_int + b_int
a = int2bin[a_int]
b = int2bin[b_int]
c = int2bin[c_int]
"""前向传播"""
# 存储每个节点的Δ输出层
y_deltas = []
# 存储每个节点的隐层(进位用)
h_list = [np.zeros((output_d, hidden_d))] # 起初进位是0
for i in range(bin_d):
# 从右到左遍历每个二进制位
X = np.array([[a[bin_d - i - 1], b[bin_d - i - 1]]])
y = np.array([[c[bin_d - i - 1]]])
# 隐层 = S(输入层 x W0 + 前一隐层)
h = sigmoid(X.dot(W0) + h_list[-1].dot(Wh))
# 输出层 = S(隐层 x W1)
o = sigmoid(h.dot(W1))
# Δ输出层 = (y - 输出层) * S'(输出层)
y_deltas.append((y - o) * sigmoid(o, deriv=True))
# 记录隐层,用于下个节点(进位)
h_list.append(h)
"""反向传播"""
# 初始化Δ隐层
h_delta = np.zeros(hidden_d)
for i in range(bin_d):
# 从左到右遍历每个二进制位
X = np.array([[a[i], b[i]]]) # 输入层
h = h_list[-i - 1] # 当前隐层
prev_h = h_list[-i - 2] # 前一隐层
y_delta = y_deltas[-i - 1] # 当前Δ输出层
# Δ隐层 = (Δ隐层 x Wh.T + Δ输出层 x W1.T) * S'(当前隐层)
h_delta = (h_delta.dot(Wh.T) + y_delta.dot(W1.T)) * sigmoid(h, deriv=True)
# 更新权重系数
Wh += prev_h.T.dot(h_delta) * alpha # += 前一隐层.T x Δ隐层
W1 += h.T.dot(y_delta) * alpha # += 隐层.T x Δ输出层
W0 += X.T.dot(h_delta) * alpha # += 输出层.T x Δ隐层
"""--------------------模型评估--------------------"""
a_int = np.random.randint(max_num / 2)
b_int = np.random.randint(max_num / 2)
c_int = a_int + b_int
a = int2bin[a_int]
b = int2bin[b_int]
c = int2bin[c_int]
h_list = [np.zeros(hidden_d)]
c_ = np.zeros_like(c) # 初始化预测值
loss = 0 # 初始化损失值
for i in range(bin_d):
X = np.array([[a[bin_d - i - 1], b[bin_d - i - 1]]])
y = np.array([[c[bin_d - i - 1]]])
h = sigmoid(X.dot(W0) + h_list[-1].dot(Wh))
o = sigmoid(h.dot(W1))
h_list.append(h)
loss += np.abs((y - o)[0])[0] # 累计损失值
c_[bin_d - i - 1] = np.round(o[0][0]) # 记录每个预测的二进制位
print('Loss:', loss)
print('Pred:', c_)
print('True:', c)
out = sum(c_[len(c_) - 1 - i] * pow(2, i) for i in range(len(c_)))
print(a_int, '+', b_int, '=', out)
- 注释
| 变量名 | 全称 | 解析 |
|---|---|---|
| w | weight coefficient | 权重系数 |
| h | hidden layer | 隐层 |
| o | output layer | 输出层 |
| d | densionality | 维度 |
| bin | binary | 二进制的 |
| delta | 第4个希腊字母,大写为Δ,小写为δ | 在数学中Δ表示变化量 |
和普通神经网络的差异
训练过程打印
import numpy as np
np.random.seed(0) # 设定随机环境
"""创建训练数据"""
bin_d = 8 # 二进制最大位数
max_num = pow(2, bin_d) # 十进制最大值
binary = np.unpackbits(np.array([range(max_num)], dtype=np.uint8).T, axis=1)
int2bin = {i: binary[i] for i in range(max_num)} # 用于整数映射到其二进制
"""sigmoid及其导数【S'(x) = S(x) * (1 - S(x))】"""
sigmoid = lambda x, deriv=False: x * (1 - x) if deriv else 1 / (1 + np.exp(-x))
"""设定超参数和网络架构"""
alpha = 0.1 # 学习速率
hidden_d = 20 # 隐层的神经元个数
input_d = 2 # 2个数相加
output_d = 1 # 2个数相加输出是1个数
# 初始化神经网络权重系数
W0 = 2 * np.random.random((input_d, hidden_d)) - 1
W1 = 2 * np.random.random((hidden_d, output_d)) - 1
Wh = 2 * np.random.random((hidden_d, hidden_d)) - 1
"""训练"""
for j in range(10001):
# 生成一组样本(a + b = c)
a_int = np.random.randint(max_num / 2)
b_int = np.random.randint(max_num / 2)
c_int = a_int + b_int
a = int2bin[a_int]
b = int2bin[b_int]
c = int2bin[c_int]
c_ = np.zeros_like(c) # 初始化预测值
loss = 0 # 初始化损失值
"""前向传播"""
# 存储每个节点的Δ输出层
y_deltas = []
# 存储每个节点的隐层(进位用)
h_list = [np.zeros((output_d, hidden_d))] # 起初进位是0
for i in range(bin_d):
# 从右到左遍历每个二进制位
X = np.array([[a[bin_d - i - 1], b[bin_d - i - 1]]])
y = np.array([[c[bin_d - i - 1]]])
# 隐层 = S(输入层 x W0 + 前一隐层)
h = sigmoid(X.dot(W0) + h_list[-1].dot(Wh))
# 输出层 = S(隐层 x W1)
o = sigmoid(h.dot(W1))
# Δ输出层 = (y - 输出层) * S'(输出层)
y_deltas.append((y - o) * sigmoid(o, deriv=True))
# 记录隐层,用于下个节点(进位)
h_list.append(h)
# 累计损失值
loss += np.abs((y - o)[0])[0]
# 记录每个预测的二进制位
c_[bin_d - i - 1] = np.round(o[0][0])
"""反向传播"""
# 初始化Δ隐层
h_delta = np.zeros(hidden_d)
for i in range(bin_d):
# 从左到右遍历每个二进制位
X = np.array([[a[i], b[i]]]) # 输入层
h = h_list[-i - 1] # 当前隐层
prev_h = h_list[-i - 2] # 前一隐层
y_delta = y_deltas[-i - 1] # 当前Δ输出层
# Δ隐层 = (Δ隐层 x Wh.T + Δ输出层 x W1.T) * S'(当前隐层)
h_delta = (h_delta.dot(Wh.T) + y_delta.dot(W1.T)) * sigmoid(h, deriv=True)
# 更新权重系数
Wh += prev_h.T.dot(h_delta) * alpha # += 前一隐层.T x Δ隐层
W1 += h.T.dot(y_delta) * alpha # += 隐层.T x Δ输出层
W0 += X.T.dot(h_delta) * alpha # += 输出层.T x Δ隐层
"""训练过程打印"""
if j % 1000 == 0:
print(str(j).center(30, '-'))
print('Loss:', loss)
print('Pred:', c_)
print('True:', c)
out = sum(c_[len(c_) - 1 - i] * pow(2, i) for i in range(len(c_)))
print(a_int, '+', b_int, '=', out)
--------------0---------------
Loss: 2.36860806313814
Pred: [0 0 0 0 0 0 0 0]
True: [1 0 1 0 0 0 0 0]
46 + 114 = 0
-------------1000-------------
Loss: 3.8972460327798943
Pred: [0 1 0 1 1 1 1 0]
True: [0 1 1 1 1 1 0 0]
79 + 45 = 94
-------------2000-------------
Loss: 3.7988105355472275
Pred: [0 0 0 0 0 0 0 0]
True: [0 1 0 1 1 0 1 0]
58 + 32 = 0
-------------3000-------------
Loss: 3.591718740829392
Pred: [0 0 0 0 0 0 0 0]
True: [0 1 0 0 1 1 1 0]
45 + 33 = 0
-------------4000-------------
Loss: 2.305327768757372
Pred: [1 0 0 1 1 0 0 0]
True: [1 0 0 1 1 0 0 0]
59 + 93 = 152
-------------5000-------------
Loss: 1.0177087227688317
Pred: [1 0 1 1 1 1 0 0]
True: [1 0 1 1 1 1 0 0]
73 + 115 = 188
-------------6000-------------
Loss: 0.6103001823550381
Pred: [1 0 0 0 0 1 1 0]
True: [1 0 0 0 0 1 1 0]
106 + 28 = 134
-------------7000-------------
Loss: 0.5356951286930459
Pred: [0 1 0 0 1 0 1 1]
True: [0 1 0 0 1 0 1 1]
30 + 45 = 75
-------------8000-------------
Loss: 0.2838521529557654
Pred: [0 1 1 0 1 1 1 0]
True: [0 1 1 0 1 1 1 0]
14 + 96 = 110
-------------9000-------------
Loss: 0.4182943229544548
Pred: [1 0 1 0 0 0 1 0]
True: [1 0 1 0 0 0 1 0]
85 + 77 = 162
------------10000-------------
Loss: 0.33523165770826124
Pred: [1 0 1 0 0 0 1 1]
True: [1 0 1 0 0 0 1 1]
120 + 43 = 163