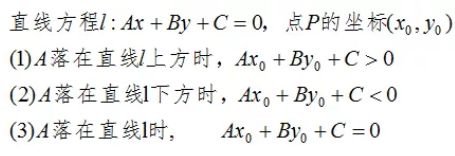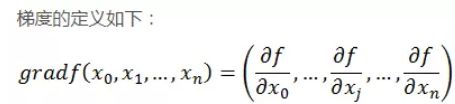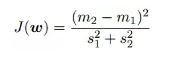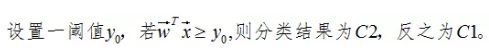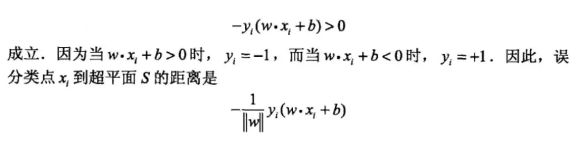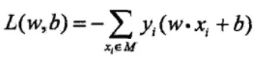线性分类模型(一):线性判别模型分析
前言
前几篇文章介绍了线性回归算法,线性分类模型分为判别式模型和生成式模型,本文首先简单复习了与算法相关的数学基础知识,然后分析各线性判别式分类算法,如最小平方法,Fisher线性判别法和感知器法,最后总结全文。
目录
1、相关的数学知识回顾
2、判别式模型和生成性模型
3、最小平方法
4、Fisher线性判别函数
5、感知器算法
6、总结
相关数学知识回顾
1、直线方程和平面方程
拓展到分类思想:直线l为分类决策方程,坐标点落在直线l上方时,则分类为C1;坐标点落在直线l下方时,则分类为C2(如下图)。
平面方程类似,在这里不展开。
2、点到直线和点到平面的距离
点到直线的距离:
点到平面的距离
拓展到分类思想:平面方程为决策方程,正确分类的情况下,当点P到决策方程的距离越大,则分类模型越好;错误分类的情况下,点P到决策方程的距离作为损失函数,损失函数最小化过程即是模型参数最优化过程。
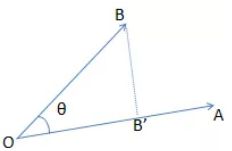
3、向量内积的数学意义
几何意义:向量A与向量B的内积等于向量A在向量B的投影与向量B的乘积,当向量B是单位向量时,则等于向量A在单位向量方向的投影,单位向量类似于基函数或者可以理解成坐标轴,即向量A在向量B的投影可理解成向量A在向量B方向的坐标,如下图,B'是B在OA坐标轴方向的投影。
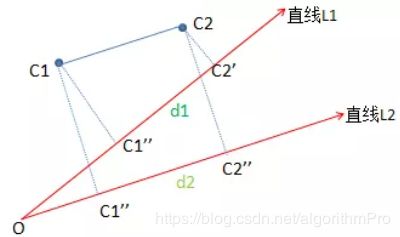
拓展到分类思想:C1与C2属于不同的类,给定一条决策性直线l,当C1与C2在直线L2的投影间距越大,则分类效果越好。增加不同类间的距离可以作为模型参数优化的方向。
如下图,C1和C2的在直线L2的投影距离|C1"C2"|大于|C1'C2'|,因此决策方程直线L2优于直线L1.
4、梯度下降法
函数f(x0,x1,...,xn)在梯度方向是函数值变化(增加或减少)最快的方向(本文只给出结论,后续文章会有详细的说明)。
拓展到分类思想:损失函数最小化过程即是模型参数最优化过程,损失函数最小化可通过梯度下降法来实现,当迭代到一定程度,损失函数收敛,则迭代结束,参数w即是要求的最优参数。
流程图如下:
判别式模型和生成性模型
我们常把分类问题分成两个阶段:推断阶段和决策阶段,对于输入变量x,分类标记为Ck。推断阶段和决策阶段具体表示为:
推断阶段:估计P(x,Ck)的联合概率分布,对P(x,Ck)归一化,求得后验概率P(Ck|x)。
决策阶段:对于新输入的x,可根据后验概率P(Ck|x)得到分类结果。
判别式模型和生成性模型的区别
判别式模型:简单的学习一个函数,将输入x直接映射为决策,称该函数为判别式函数。
生成式模型:推断阶段确定后验概率分布,决策阶段输出分类结果,生成式模型包含两个阶段。
本文介绍判别式线性分类模型的三种算法。
最小平方法
最小平方法与最小二乘法的算法思想类似,K类判别函数由K个方程决定,
训练集![]() ,K类判别函数为
,K类判别函数为![]() ,k=1,2,...,K
,k=1,2,...,K
参数矩阵为![]() ,目标矩阵
,目标矩阵![]() 。
。
求得最优参数w后,输入变量x所属K类的判别方法如下:
Fisher线性判别函数
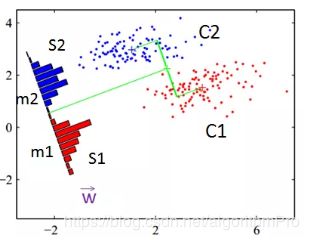
第一节讲到,若两个类在同一个决策方程的投影距离相隔越大,则该决策方程越好。再深入一点,相同类投影到决策方程的方差越小,则该决策方程越好,方差代表类投影到决策方程的聚集程度。这就是Fisher线性判别法参数优化思想。
参数优化思想:同类样本投影到决策方程的方差最小,不同类样本投影到决策方程的均值间隔最大。用表达式J(w)表示,J(w)越大越好。
如下图:
其中,m1,m2分别表示不同类在决策方程的投影均值;S1,S2分别表示不同类投影到决策方程的方差。
求得最优参数w后,输入变量x所属类的判别方法如下:
感知器算法
感知器算法的目的是找到能够准确分离正负样本训练数据集的超平面。
超平面定义:
感知器学习策略:
对训练数据集某一样本点(x,y),若wx+b>0,则y=1;若wx+b<0,则y=-1;
即感知机模型为:
因此,对于误分类的数据(xi,yi)来说:
因此,感知器学习策略是最小化误分类点到平面S的距离,不考虑分母项。
假设训练数据集有M个误分类点,损失函数为:
运用梯度下降算法最小化损失函数L(w,b)。
设学习率η,感知器学习策略步骤:
(1)、选取处置w0,b0;
(2)、选取训练集(xi,yi);
(3)、如果yi(w*xi+b)<=0,则更新权值参数w,b:
(4)、转至(2),直至训练数据集没有误分类点,得到超平面最优参数w,b。
感知机学习算法由于采用不同的初值或选取不同的误分类点,参数解可能不同(例题可参考《统计学习方法》)。
因此,对某一输入点,若感知机模型大于0,则分类为1;反之分类为-1。
总结
本文介绍了线性判别分类的三种方法,第一种判别方法是根据点到判别函数的距离来分类,,第二种方法是根据输入样本在判别函数的投影距离进行分类,第三种方法则采用感知机模型进行分类。
参考
Christopher M.Bishop <
李航 《统计学习方法》