softmax with cross-entropy loss求导(转载＋细节整理)

softmax 函数
softmax(柔性最大值)函数，一般在神经网络中， softmax可以作为分类任务的输出层。

其实可以认为softmax输出的是几个类别选择的概率，比如我有一个分类任务，要分为三个类，softmax函数可以根据它们相对的大小，输出三个类别选取的概率，并且概率和为1。

即总共有$k$类,必有:
$$\sum _{k=1}^C{y}_i=1$$

为了方便下面的推导，先来个图示：

----------------------------------------
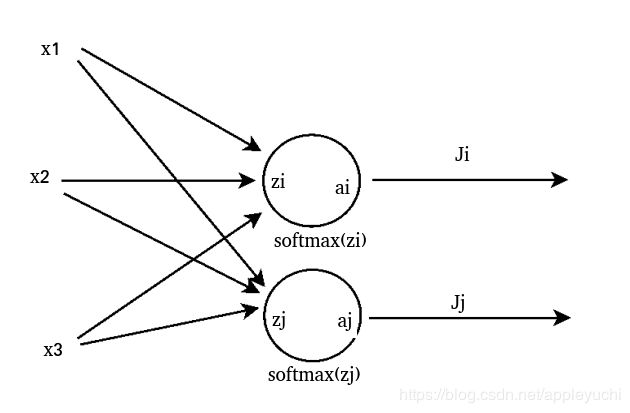
softmax函数的公式是这种形式：
$$a_i=\frac{e^{z_i}}{{\sum }_k^{e^{z_k}}}$$

其中：
$w_{ij}$:第$i$个神经元的第$j$个权重，
b:偏移值。
$z_i$:该网络的第$i$个输出。

在$z_i$后面施加softmax函数,得到$a_i$

损失函数使用Cross_Entropy
----------------------------------------
$$J=-\sum _i{y}_{i}ln{a}_i$$
其中：
$a_i$:模型预测值
$y_i$:预期数值

当二分类时,有

$$\frac{1}{N}\sum _{n=1}^N[p_{n}log{q}_n+(1-p_n)log(1-q_n)]$$
其中：
$N$:数据集的总数
$p_n$:真实分布
$q_n$:预测分布
----------------------------------------------

这篇博客中，我们的目标函数是：
$$\frac{\partial J}{\partial z_i}$$
$$＝\sum _j(\frac{\partial J_j}{\partial a_j}\frac{\partial a_j}{\partial z_i})$$

其中：
$$\frac{\partial J_j}{\partial a_j}$$
$$=-\frac{-y_j\cdot ln{a}_j}{\partial a_j}$$
$$=-y_j\frac{1}{a_j}$$

$$\frac{\partial a_j}{\partial z_i}$$
$$=\frac{\partial [\frac{e^{z_j}}{{\sum }_k{e}^{z_k}}]}{\partial z_i}$$

下面分情况，这里之所以要分情况是求导的规律来决定的：

$$\frac{\partial [\frac{e^{z_j}}{{\sum }_k{e}^{z_k}}]}{\partial z_i}(1)$$
为了处理式(1)，根据：
$f(x)=\frac{g(x)}{h(x)}$
$$f^{\prime }(x)=\frac{g^{\prime }(x)h(x)-g(x)h^{\prime }(x)}{|h(x){|}^2}$$

所以这里：
$g(x)=e^{z_j}$
$h(x)={\sum }_k{e}^{z_k}$

①$i=j时,g^{\prime }(x)=e^{z_j},h^{\prime }(x)=e^{z_j}$
②$i$≠j$时,g^{\prime }(x)=0,h^{\prime }(x)=e^{z_j}$

由此处理式(1)得到：
①$i=j时$
$$\frac{\partial a_j}{\partial z_i}=\frac{e^{z_i}{\sum }_k{e}^{z_k}-(e^{z_i}{)}^2}{[{\sum }_k{e}^{z_k}{]}^2}=a_i-a_i^2$$

①$i$≠$j时$
$$\frac{\partial a_j}{\partial z_i}=\frac{-(e^{z_j})(e^{z_i})}{[{\sum }_k{e}^{z_k}{]}^2}=-a_j\cdot a_i$$

总结下：
$$\frac{\partial J}{\partial z_i}$$
$$=\sum _j(\frac{\partial J_j}{\partial a_j}\frac{\partial a_j}{\partial z_i})$$
$$=\sum _{i=j}[(\frac{-y_j}{a_j})(a_i-a_i^2)]+\sum _{i̸=j}[(\frac{-y_j}{a_j})(-a_j{a}_i)]$$
$$=-y_i(1-a_i)+\sum _{i̸=j}[y_j{a}_i]$$
$$=-y_i+a_i\sum _j{y}_j$$
$$\because \sum _j{y}_j=1(因为所有情况的概率和为1)$$
$$\therefore 原式＝-y_i+a_i$$

参考链接：
https://blog.csdn.net/Charel_CHEN/article/details/81266838
https://blog.csdn.net/qian99/article/details/78046329
https://zhuanlan.zhihu.com/p/27223959
http://shuokay.com/2016/07/20/softmax-loss/