动态规划初识（从dfs到dfs优化到动态规划顺推和逆推）

    思想：动态规划是通过组合子问题来解决问题的，是用于求解包含重叠子问题的最优化问题的方法。

 

入门题目：数字三角形

题目描述：给出了一个数字三角形。从三角形的顶部到底部有很多条不同路径。对于每条路径，把路径上面的数加起来可以得到一个和，你的任务就是找到最大的和。

       注意：路径上的每一步只能从一个数走到下一层上和它最近的左边的那个数或者右边的那个数。

       如：

7

3   8

8   1   0

2   7   4   4

4   5   2   6   5

一、深度优先搜索

此题可以从深度优先搜索入手，深度搜索的概念简单说就是竟可能深入一条路径直到遇到障碍，返回上一步继续下一路径。因此要想深入，（1）首先需要不断到达下一步，也就可以使用递归实现，要想能够返回上一步必须要障碍，（2）所以必须要结束一条路径的条件。

代码如下：

#include 
using namespace std;
int tri[410][410];
int N;
static int m=0,l=0;
int dfs(int x,int y)
{
	m++;
	cout<N || y>N) return 0;
	else 
	{
		l++;
		return max(dfs(x+1,y),dfs(x+1,y+1))+tri[x][y];
	}
}
int main()
{
	cin>>N;
	memset(&tri,0,sizeof(tri));
	for(int i=1;i<=N;i++)
		for(int j=1;j<=i;j++)
			cin>>tri[i][j];
	int maxsum = dfs(1,1);
	cout<

程序通过第一个点(1,1)出发，不断向下递归找到最大和。程序中使用全局变量m表示dfs函数调用次数，l表示max函数调用次数，并且通过cout得到dfs调用顺序。

输入输出案例一：

分析：

dfs函数调用7次（由输出可知max()函数内部为逗号运算符，先执行右边部分），max调用三次：

路径一：1,1  2,2  3,3  3,2  （先从1,1一直到3,3；然后回到2,2转到3,2；最后max比较得到2,2）

路径二：2,1  3,2  3,1  （2,2回到1,1然后转到2,1；然后到3,2得到要比较的第一个值；然后回到2,1到3,1得到比较的第二个值，使用max进行比较得到2,1）

最后再将2,1和2,2使用max函数进行比较得到最后的最大和为15。

输入输出案例二：

此输入输出案例分析和上面类似，但是我们可以发现重复计算的地方为4,3；3,2；4,2；相比上面案例重复计算量增加了，因此我们可以想象，当三角形足够大时时间复杂度会相当高，此时我们需要做一些优化，将计算过的点通过数组存储起来，可以大大节省时间。

二、深度优先搜索+记忆优化

通过将计算所得结果存储于数组，当需要计算x,y点的数据是首先判断其res是否已经计算过，是则直接返回，否则继续计算。

代码如下：

/*dfs+优化*/
#include 
using namespace std;
int tri[410][410];
int res[410][410]; 
int N;
static int m=0,l=0;
int dfs(int x,int y)
{
	m++;
	cout<N || y>N) return 0;
	else 
	{
		l++;
		return res[x][y] = max(dfs(x+1,y),dfs(x+1,y+1))+tri[x][y];
	}
}
int main()
{
	cin>>N;
	memset(&tri,0,sizeof(tri));
	memset(&res,-1,sizeof(res));
	for(int i=1;i<=N;i++)
		for(int j=1;j<=i;j++)
			cin>>tri[i][j];
	int maxsum = dfs(1,1);
	cout<

输入输出案例一：

 

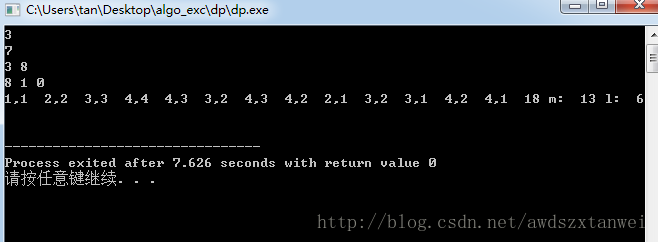
相比没优化的dfs算法，此时m只需要13次，而max只要6次。因此经过优化的dfs算法要优于dfs算法。

三、动态规划顺推

经过上面的dfs，我们可以知道要想得到最大路径和只要res数组最后一行中最大元素即为最大路径和。而每一个点[x][y]的最大路径和只可能来自于[x-1][y]或者[x-1][y-1]两个地方。因此对于x,y点我们只需要考虑上一行两个点大小即可，所以有：

res[x][y] = max(res[x-1][y],res[x-1][y-1])+tri[x][y]

所以我们只需要从第一个点开始逐步求得res[][]数组，最后res[][]数组最后一行最大值即为所求结果。

代码：

/**********dp正向计算**********/
#include 
#include 
#include 
using namespace std;
int tri[410][410];
int res[410][410];
int main()
{
    int n,i,j;
    cin>>n;
    memset(res,0,sizeof(res));
    for(i=0;i>tri[i][j];
    }
    res[0][0] = tri[0][0]; 
    for(i=1;i

四、动态规划逆推

上面介绍了顺推，也可以使用逆推，从下到上，把最下面一层当做开始第一层，计算res[x][y]状态数组时，其值只可能来自于res[x+1][y]和res[x+1][y+1]两个状态，因此有如下状态转移方程：

res[x][y] = max(res[x+1][y],res[x+1][y+1])+tri[x][y]

到最后一个res的时候就是最大的路径和。

代码：

/**********dp反向计算**********/
#include 
#include 
#include 
using namespace std;
int tri[410][410];
int res[410][410];
int main()
{
    int n,m,i,j;
    cin>>n;
    memset(res,0,sizeof(res));
    for(i=0;i>tri[i][j];
    }
    for(i=n-1;i>=0;i--)
        for(j=0;j<=i;j++)
            res[i][j]=tri[i][j]+max(res[i+1][j],res[i+1][j+1]);
    cout<

总结：dfs和dp还是有区别的，dfs主要是一种遍历方法，而dp是一种思想方法，dp主要是将要求解的内容分解为小问题，然后通过状态转移得到结果；dfs只是深度优先遍历各节点判断结果。