【数据结构】二叉树面试题总结
为了对二叉树的知识进行巩固,今天我们来解析5道二叉树的经典面试题。
这五道面试题如下:
- 求二叉树中最远两个结点的距离;
- 判断一棵树是否是完全二叉树;
- 由前序和中序遍历序列重建二叉树 (前序序列:1 2 3 4 5 6 - 中序序列:3 2 4 1 6 5);
- 求二叉树两个结点的最近公共祖先;
将二叉搜索树转化成有序的双向链表;
现在我们来对这五道题进行分析:
求二叉树中最远的两个节点之间的距离
这道题如果没有进行全面的分析,都以为只有一下一种情况:
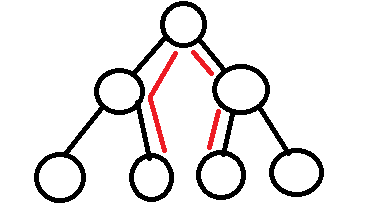
这时,我们只需要分别求出左右子树的高度然后相加再加1(根节点),就能得到最远的两个节点之间的距离了。
经过仔细分析,我们发现还有以下这种情况:
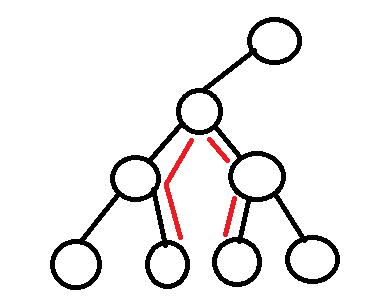
时间负杂度为O(N*N)的解法
当二叉树的根节点只有一颗子树时,这时候二叉树最远节点的距离应该产生在子树的左右子树高度或这棵树的高度再到根节点之间的距离两者之间的,所以我们要求一颗树最远的两个节点之间的距离,就需要求出这棵树根节点的子树的高度加上子树根节点到这棵树根节点的距离和子树中最远的两个节点之间的距离,两者的最大值就是这棵树最远的两个节点之间的距离了。所以我们要求解一棵树最远的两个节点之间的距离,就要去求子树的高度和子树的最远的两个节点之间的距离,直到我们求到子树的根节点为NULL为止。
上面这种解法运用到了二叉树先序遍历的思想,先求根节点的最远两个节点之间的距离,再去求左子树和右子树最远两个节点之间的距离。下面我们来看一种时间复杂度为O(N)的解法
时间复杂度为O(N)的解法
这种解法就需要用到二叉树后序遍历的思想了,我们碰到树的根节点先不去求当前根节点最远的两个节点之间的距离,转而去求它左右子树最远的两个节点之间的距离和左右子树的高度,最后再来求当前根节点最远的两个节点之间的距离。
我们直接给出最优解法的代码:
//时间复杂度为O(N^2)的算法
size_t DepthOfNode(BinaryTreeNode<int>* node)
{
if (node == NULL)
{
return 0;
}
//分别求左右子树
size_t Left = DepthOfNode(node->_Left) + 1;
size_t Right = DepthOfNode(node->_Right) + 1;
/*cout << "Left:"<
return Left > Right ? Left : Right;
}
void _DisTanceOfNode(Node* root, size_t& LeftHigh, size_t RightHigh, size_t& Max);
size_t DisTanceOfNode(BinaryTree<int>& tree)
{
size_t LeftHight = 0;
size_t RightHight = 0;
size_t Max = 0;
_DisTanceOfNode(tree.ReturnRoot(), LeftHight, RightHight,Max);
return Max;
}
时间复杂度为O(N*N)的算法
void _DisTanceOfNode(Node* root, size_t& LeftHigh, size_t RightHigh,size_t& Max)
{
if (root == NULL)
return;
if (root->_Left == NULL)
LeftHigh = 0;
if (root->_Right == NULL)
RightHigh = 0;
if (root->_Left != NULL)
_DisTanceOfNode(root->_Left, LeftHigh, RightHigh, Max);
if (root->_Right != NULL)
_DisTanceOfNode(root->_Right, LeftHigh, RightHigh, Max);
LeftHigh = DepthOfNode(root->_Left);
RightHigh = DepthOfNode(root->_Right);
//更新当前根节点的最远两个节点之间的距离
if (LeftHigh + RightHigh + 1 > Max)
Max = LeftHigh + RightHigh + 1;
}
void _DisTanceOfNode(Node* root, size_t& LeftHigh, size_t RightHigh, size_t& Max)
{
if (root == NULL)
{
return;
}
_DisTanceOfNode(root->_Left, LeftHigh, RightHigh, Max); //递归求左子树最远两个节点之间的距离
_DisTanceOfNode(root->_Right, LeftHigh,RightHigh, Max); //求右子树
LeftHigh = DepthOfNode(root->_Left);
RightHigh = DepthOfNode(root->_Right);
if (LeftHigh + RightHigh + 1 > Max)
Max = LeftHigh + RightHigh + 1;
}
void Test1()
{
int b[] = { 1, 2, 3, 5, '#', '#', '#', 4, '#', 6, '#', '#', '#' };
int a[15] = { 1, 2, '#', 3, '#', '#', 4, 5, '#', 6, '#', 7, '#', '#', 8 };
BinaryTree t1(b, sizeof(b) / sizeof(b [0]), '#');
t1.InOrder();
t1.LevelOrder();
cout << "树中最远的两个节点之间的距离是?" << DisTanceOfNode(t1) << endl;
} 重建二叉树
题目中给出了先序遍历和中序遍历,让根据遍历二叉树的序列来对这颗二叉树进行构建,要重建这颗二叉树我们就得要要建立二叉树的根节点,然后再分别构建这颗二叉树的左右子树,二叉树的根节点元素就是前序序列的第一个元素,这样我们根节点就能构建完成,接下来我们在中序遍历中找到根节点元素,这个元素之前的序列就为左子树的中序遍历,之后的序列就为右子树的中序遍历,接下来我们去递归分别创建左右子树就可以了
struct BinaryTreeNode
{
int _value;
BinaryTreeNode* _Left;
BinaryTreeNode* _Right;
BinaryTreeNode(const int& x)
:_value(x)
, _Left(NULL)
, _Right(NULL)
{}
};
typedef BinaryTreeNode Node;
Node* CreateBinaryTree(vector<int>& front, vector<int>& mid,int size)
{
assert(front.size() == mid.size());
if (size <= 0||front.size()==0||mid.size()==0) //递归终止条件
return NULL;
//先创建根节点
Node* root = new Node(front[0]); //前序遍历的第一个节点为根节点的元素
//在中序遍历中找到根节点元素的所在位置
int index = 0;
for (index = 0; index < size; index++)
{
if (front[0] == mid[index])
break;
}
if (index == size)
{
cout << "Invaid Input!!!创建失败" << endl;
exit(0);
}
//构建子序列
vector<int> b; //中序
vector<int> a; //先序遍历
for (int i = 0; i < index; i++)
{
b.push_back(mid[i]);
a.push_back(front[i+1]);
}
//递归创建左子树
root->_Left = CreateBinaryTree(a, b, a.size());
a.clear();
b.clear();
for (int i =index+1; i < size; i++)
{
b.push_back(mid[i]);
a.push_back(front[i]);
}
//递归创建右子树
root->_Right = CreateBinaryTree(a, b, a.size());
a.clear();
b.clear();
return root;
}
判断一棵树是否是完全二叉树
什么是完全二叉树呢? 如下:
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
那么我们怎么判断一棵树是否是完全二叉树呢,我们可以用一个队列,通过层序遍历的方式把二叉树所有的节点都先入队(包含空节点),当我们出队的时候如果pop出来了空节点如果队列中剩余的所有节点都为NULL,那么这棵树就是完全二叉树,如果队列中还有非NULL节点,那么这棵树就不是完全二叉树。
bool _LevelOrder(BinaryTreeNode<int>* root)
{
queue求两个节点的最近公共祖先
求二叉树的任意两个节点的最近公共祖先问题,包含以下两种情况
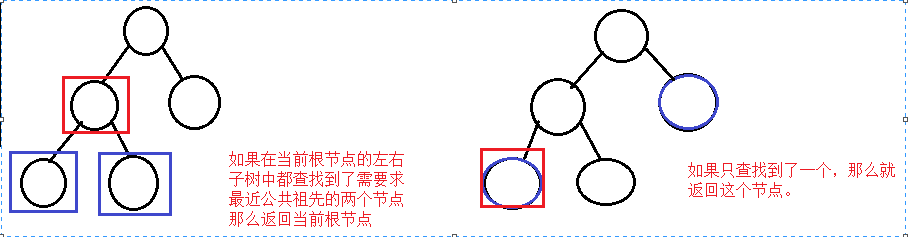
1:这两个节点都不是最近公共祖先。
2:这两个节点有一个是公共祖先。

方法一
我们可以借助STL容器来实现这个问题,比方说一个顺序表,我们从根节点开始,把从根节点到要查找的节点之间的节点都pusn_back到vector中,这样做等于说我们拿到了从根节点到需要求公共祖先的两个节点的两条路径,我找到这两条路径中最后一个相等的节点,这个节点就是这两个节点的最近公共祖先。
bool FindPath(BinaryTreeNode<int>* root, vector<int>& path,const int& value)
{
/*寻找到达某一个节点的路劲找到了返回true并保存路劲*/
if (root == NULL)
{
return false; //树为NULL则路劲不存在
}
path.push_back(root->_Data);
if (root->_Data == value)
return true;
/*在左右子树中查找*/
bool IfFind = FindPath(root->_Left, path, value) || FindPath(root->_Right, path, value);
if (IfFind)
return true;
path.pop_back(); //如果在该节点下没有找到就删除路劲当中的节点
return false;
}
Node* FindLCA(BinaryTree<int>& t,const int& n1,const int& n2)
{
vector<int> Findn1Path;
vector<int> Findn2Path;
if (FindPath(t.ReturnRoot(), Findn1Path, n1) && FindPath(t.ReturnRoot(), Findn2Path, n2))
{
int index = -1; //记录最后一个相等键值的位置
int size = Findn1Path.size() > Findn2Path.size() ? Findn2Path.size() : Findn1Path.size();
for (int i = 0; i < size; i++)
{
if (Findn1Path[i] != Findn2Path[i])
break; //找到第一个不相等的键值
index = i;
}
if (index == -1)
return NULL; //index=0 表示没有相等的键值
else
return new Node(Findn1Path[index]);
}
cout << "两个键值中有一个键值在二叉树中没有节点" << endl;
return NULL;
}
void Test4()
{
int a[15] = { 1, 2, '#', 3, '#', '#', 4, 5, '#', 6, '#', 7, '#', '#', 8 };
BinaryTree<int> t(a, sizeof(a) / sizeof(a[0]), '#');
cout<3, 5)->_Data<cout << FindLCA(t, 7, 8)->_Data << endl;
} 方法二:不需要容器的解法
Node* _GetAncestor(Node* root, Node* node1, Node* node2)
{
if (root == NULL)
return NULL;
Node* Left = _GetAncestor(root->_Left, node1, node2);
Node* Right = _GetAncestor(root->_Right, node1, node2);
if (Left&&Right) //如果Left和Right都不为NULL 则root节点为他们的最近祖先
return root;
if (root == node2)
return node2;
if (root == node1)
return node1;
if ((Right == NULL) && Left)
return Left;
if ((Left == NULL) && Right)
return Right;
return NULL;
}
Node* GetAncestor(BinaryTree<int>& tree, Node* node1, Node* node2)
{
//assert(node1);
//assert(node2);
Node* ancestor = _GetAncestor(tree.ReturnRoot(), node1, node2);
return ancestor;
}
void Test2()
{
int b[] = { 1, 2, 3, 5, '#', '#', '#', 4, '#', 6, '#', '#', '#' };
int a[15] = { 1, 2, '#', 3, '#', '#', 4, 5, '#', 6, '#', 7, '#', '#', 8 };
BinaryTree<int> t1(b, sizeof(b) / sizeof(b[0]), '#');
t1.InOrder();
t1.LevelOrder();
cout << "最近的祖先是?" << GetAncestor(t1,t1.Find(5),t1.Find(7))->_Data<< endl;
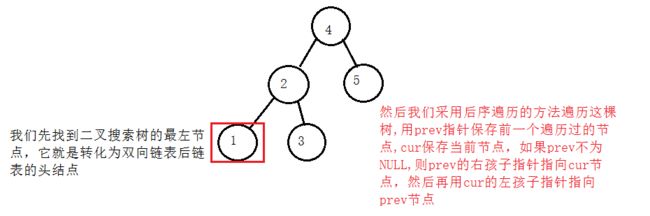
}将一颗二叉搜索树转化为双向链表
void _TreeToList(Node* cur, Node*& prev)
{
if (cur == NULL)
return;
_TreeToList(cur->_left, prev);
cur->_left = prev;
if (prev != NULL)
prev->_right = cur;
prev = cur;
_TreeToList(cur->_right, prev);
}
Node* TreeToList(BinarySearchTree<int>& tree)
{
Node* Head = tree.ReturnRoot();
while (Head->_left)
{
Head = Head->_left; //二叉搜索树的最左节点就是单链表的第一个节点
}
Node* Prev = NULL;
Node* cur = tree.ReturnRoot();
_TreeToList(cur, Prev);
return Head;
}
void OrDerList(Node* root)
{
assert(root);
while (root)
{
cout << root->_key << " ";
root = root->_right;
}
cout << endl;
}
void Test5()
{
BinarySearchTree<int> t;
t.Insert(5);
t.Insert(4);
t.Insert(7);
t.Insert(3);
t.Insert(6);
t.Insert(9);
t.Insert(2);
t.Insert(0);
t.Insert(1);
t.Insert(8);
t.InorderR();
Node* head=TreeToList(t);
OrDerList(head);
}