【深度学习入门】——亲手实现图像卷积操作
深度学习中有一个很重要的概念就是卷积神经网络 CNN,卷积神经网络中又有卷积层、池化层的概念。尤其是卷积层,理解难度比较大,虽然书中或者是视频中都有详细介绍过它的基础概念,但对于求知欲望很强烈的我,我总心里痒痒的,总想亲手实现,看看效果,怕的就是自己会眼高手低,做技术人最可怕的就是眼高手低。所以,我打算用 python 来亲自验证一遍。
什么是卷积?
卷积(convolution)是数学知识,概率论和信号与系统中都有涉及。卷积的公式如下:
连续信号:
y ( t ) = x ( t ) ∗ h ( t ) = ∫ − ∞ ∞ x ( p ) ∗ h ( p − t ) y(t)=x(t)\ast h(t)=\int_{-\infty}^\infty x(p)*h(p-t) y(t)=x(t)∗h(t)=∫−∞∞x(p)∗h(p−t)
离散信号
y ( n ) = ∑ i = − ∞ ∞ x ( i ) ∗ h ( n − i ) y(n) = \sum_{i=-\infty}^{\infty} x(i)*h(n-i) y(n)=i=−∞∑∞x(i)∗h(n−i)
卷积会由两个原函数产生一个新的函数,两个函数之间的这种操作就称着卷积,卷积的数学意义与物理意义这里不过多讲述,因为展开来讲的话可以另外写一篇博文了,不熟悉的同学大家点击这里,我们把目标放在图像的卷积操作之上。
需要说明的是,图像处理中的卷积对应的是离散卷积公式。
图像的卷积操作
我们假设有一张图片,我们称之为输入图片,我们对原图片进行某种卷积操作之后会得到另外一张图片,我们称这张图片为输出图片。

一般的,我们通过对图片进行卷积操作,可以对图片进行某种效果的增强或者是减弱。比如说图片的模糊、锐化、浮雕效果等等。

当然,也可以发现图片中某些特征,如查找物体的边缘信息。而深度学习做的最重要的工作之一就是发现数据的特征,这也是卷积神经网络诞生的原因。
那么对于一张图片而言,卷积操作是如何进行的呢?
什么是卷积核?
一张图片进行卷积后的显示效果,绝大部分取决于它的卷积核(kernel)。那么,什么是卷积核呢?
其实卷积核并没有什么神秘的,它是一个 2 维数组。它的行数和列数相同并且数值为奇数。

上面就是一个 3x3 的卷积核,它的核大小(kernel size) 为 3。它里面的元素值代表不同的权值。
一般而言,卷积核里面所有元素之和等于 1,当然你也可以不让它等于 1,大于 1时生成的图片亮度会增加,小于 0 时生成的图片亮度会降低。
那么,卷积核是如何作用在一张图之上的呢?
一句话描述就是:针对输入图片中单个像素,将它的值由周围邻近的像素值加权平均。而这种加权平均的操作产生的新的像素值按照次序可以产生一张新的输出图片。
需要注意的是,在深度学习当中,只需要逐元素相乘再相加就可以了,不需要对结果取均值,我在本文采取求平均数,只为了示例的演示效果
再来说说何为加权平均?
[1,2,3,4,5]
有 5 个数,加权平均就是
( 1 ∗ w 1 + 2 ∗ w 2 + 3 ∗ w 3 + 4 ∗ w 4 + 5 ∗ w 5 ) ÷ 5 (1*w_1+2*w_2+3*w_3+4*w_4+5*w_5)\div5 (1∗w1+2∗w2+3∗w3+4∗w4+5∗w5)÷5
w i w_i wi 代表权值,如果所有的 w w w 为 1,则上面式子的等于 3。 w w w 是可以取不同的值的。
上面说过,卷积核里面的数值代表权重,那么它又是针对像素如何做加权平均的呢?
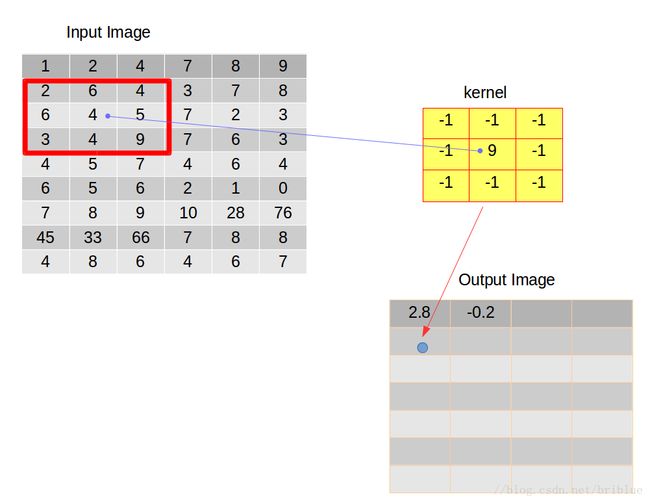
假设有这么一张图片,如下图左,卷积核如下图右。
卷积操作要求,开始的时候将它们在左上角对齐。
然后,逐元素相乘再相加,累加得到的数值再除以元素的数量,得到平均值放在输出图像矩阵的第一个元素位置上。
在第一次操作之后,我们需要重复刚才这种行为,于是我们选择将卷积核向右滑动 1 个距离,当然我们也可以选择向右滑动更多的距离,而这种距离也有个专业的名词叫做跨度(strides),也有人叫它步长。

如上图,我们将卷积后的结果放在输出的图像矩阵的第二个位置。
卷积核向右滑动是有条件的,当卷积核的右边缘超过输入图像的右边缘时,就需要考虑向下滑动了。

之后,卷积核不能再向右边滑动时,就需要重新与输入图像左对齐,并且在前面的基础上向下滑动一个跨度,跨度由我们开发人员自主决定,本文实验的跨度都取值为 1,左对齐之后重复上面叙述的卷积行为向右滑动,然后向下滑动。不停循环。
整个卷积行为终止的条件是卷积核需要向下滑动的时候,但它的下边缘已经超出了输入图像的下边缘。
此时,我们经过操作得到的输出图像就是我们这次卷积后的结果。
卷积后的图像尺寸
细心的同学可能已经发现了,卷积过程中,输入图片和输出图片的尺寸貌似是不一样的。
一般情况,输出图片的尺寸要比输入图片的尺寸小,并且,它们之间的关系其实很容易用公式推算出来。
我们假定输入图片尺寸为 m x n,输出的图片尺寸为 l x c,跨度用 stride 表示,卷积核大小用 k 表示,则有下面公式。
l = ( m − k ) / s t r i d e + 1 l = (m - k ) / stride + 1 l=(m−k)/stride+1
c = ( n − k ) / s t r i d e + 1 c = (n - k ) / stride + 1 c=(n−k)/stride+1
大家仔细琢磨一下,相信很快就能理解明白。
刚刚说了,一般而言,输出图片的尺寸要比输入图片的尺寸小,那么有同学可能会问,如果我想输出图片的尺寸跟输入图片不发生变化可以吗?
答案是肯定的,这涉及了对输入图片的 padding 操作。
padding
如果要输入图像核输出图像尺寸保持一致,经常的做法是在卷积之前认为扩大输入图像的尺寸。也就是在输入图片外围补 0。
但是怎么个补法呢?比如左边补几个 0? 上面补几个 0 ?
以左右方向为例,我们根据上面的公式可以推断出总共需要补充的 0 的个数。
c o u n t = m − l = m − ( m − k ) / s t r i d e − 1 count = m - l = m - (m - k)/stride - 1 count=m−l=m−(m−k)/stride−1
我们假设跨度为 1,则 count 的值就是 k - 1 。
博文的示例中,输入图片尺寸是 9 x 6,输出图片尺寸是 7 x 4。核大小是 3.
于是在横向,count 是 k - 1,也就是 2。我们可以让左边补 1 个 0,右边补 1 个 0。
但如果 count 结果为奇数呢,比如 5 ,那么我们可以让一边多一点,另一边少补一点 ,比如左边数值等于 c e i l ( c o u n t / 2 ) ceil(count/2) ceil(count/2) ,ceil 表示向上取整。右边数值等于 c o u n t / 2 count / 2 count/2,于是左边等于 3,右边等于 2。 这代表着在输入图片矩阵当中每一行左边扩充 3 个 0,右边扩充 2 个 0。
同理,可以求得图片在竖直方向应该补充 0 的数量。
经过 padding 之后再进行卷积,输出图片的尺寸就能够和输入图片保持一致。
这里有一张很直观的动图。图片出处
编码实践
经过上面的介绍,我们已经具备了图像卷积的基本理论,现在让我们开始通过代码论证吧。
示例代码采用 python 语言,当然你不熟悉 python 语言的话,你可以换成其他语言其实也是可以的,比如 Matlab。
我们先引进 numpy 和 matplotlib.pyplot。
import numpy as np
import matplotlib.pyplot as plt
引进 numpy 的目的是因为它提供了极为便利的数组和矩阵操作,而 matplotlib.pyplot 可以轻松实现图标绘制,这在机器学习或者是深度学习过程当中是很重要的,因为数据的可视化有助于我们理解算法和调试算法。
我们然后需要一张测试图片。
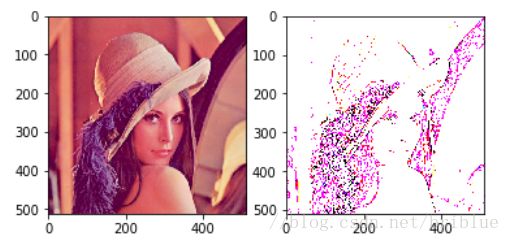
srcImg = plt.imread('../res/images/lena.jpg')
这是一张很出名的照片,在计算机视觉当中大家都喜欢用它进行测试,模特的名字就叫做 lena,大家有兴趣可以搜索它的相关信息。
输入图片的尺寸是 512 x 512 x 3,512 就它的宽高,3 代表了 RGB 3 个颜色通道。
然后,我们构建一个 3 x 3 的卷积核。
test_kernel = np.array([[-1,-1,-1],
[-1,9,-1],
[-1,-1,-1]])
在示例代码中,我们卷积操作时,跨度为 1。根据前面介绍的公式,我们很容易根据输入图片矩阵去构建输出图片的图像矩阵。
def generate_dst(srcImg):
m = srcImg.shape[0]
n = srcImg.shape[1]
n_channel = srcImg.shape[2]
dstImg = np.zeros((m-test_kernel.shape[0]+1,n-test_kernel.shape[0]+1,n_channel ))
return dstImg
注意的是,构建输出图片图像矩阵的时候,它的通道和输入图片是一致的。
有了输入图片,构建了输出图片的数据结构,我们就可以开始编写卷积操作了。
def conv_2d(src,kernel,k_size):
dst = generate_dst(src)
print dst.shape
conv(src,dst,kernel,k_size)
return dst
src 代表输入图片,kernel 自然就是卷积核,k_size 就是卷积核的大小,这里为 3。
上面的代码构建了输出图片的数据结构,并在内部调用了conv()方法。
def conv(src,dst,kernel,k_size):
for i in range(dst.shape[0]):
for j in range(dst.shape[1]):
for k in range(dst.shape[2]):
value = _con_each(src[i:i+k_size,j:j+k_size,k],kernel)
dst[i,j,k] = value
前面的理论知识,介绍过,卷积操作需要滑动卷积核重复进行。
最里面的嵌套表示,对每一个颜色通道都需要进行卷积操作。你可以想象一下输入图片分成了 3 份,每一份尺寸同原图片一样,他们的叠加形成了原图。
不然看出,核心方法是 _con_each()
def _con_each(src_block,kernel):
pixel_count = kernel.size;
pixel_sum = 0;
_src = src_block.flatten();
_kernel = kernel.flatten();
for i in range(pixel_count):
pixel_sum += _src[i]*_kernel[i];
return pixel_sum / pixel_count;
注意它的输入参数,src_block 代表的是从输入图片上截取下来的像素块。它的尺寸同卷积核一样。那它是怎么截取下来的呢?请看下面的代码
src[i:i+k_size,j:j+k_size,k]
src 是 numpy 中的 ndarray 对象,先前说了它极其方便对数组和矩阵进行操作,这行代码表示,从原数组中截取起始坐标为 (i,j),宽高都为 k_size 的数据块。
我们再看 _con_each()方法,它进行了逐元素相乘,累计相加的操作,最终的数值还要求平均。
但我们知道,RGB 模式中,数值的取值范围是 0 ~ 255,如果超出这个范围就应该截断,所以我们需要优化下程序。
def _con_each(src,kernel):
pixel_count = kernel.size;
pixel_sum = 0;
_src = src.flatten();
_kernel = kernel.flatten();
for i in range(pixel_count):
pixel_sum += _src[i]*_kernel[i];
value = pixel_sum / pixel_count
value = value if value >0 else 0
value = value if value < 255 else 255
return value;
小于 0 时,像素值取 0,大于 255 时取 255,其它情况保持现值。
需要注意的是,在 python 中三目运算和其它编程语言有点不一样。
比如我在 Java 中这样写:
a = a > 0 ? 1 : -1
在 python 中需要这样写。
a = 1 if a > 0 else -1
现在,我们卷积操作的函数也完成了,我们可以测试一下。
def test_conv(src,kernel,k_size):
plt.figure()
#121 1 代表 1行,2 代表 2 列,最后的 1 代表 图片显示在第一行第一列
plt.subplot(121)
plt.imshow(src)
dst = conv_2d(src,kernel,k_size)
#121 1 代表 1行,2 代表 2 列,最后的 2 代表 图片显示在第一行第发给列
plt.subplot(122)
plt.imshow(dst)
plt.show()
在这个测试函数中,将输入图像和输出图像在一个图标中并排显示。然后我们调用这个函数。
test_conv(srcImg,test_kernel,3)
卷积效果取决于卷积核,它的大小不同,里面的数值不同,卷积后的效果就会不同的,大家可以自行设计不同的卷积核进行试验。
CNN 中的卷积操作
在 CNN 中,每一个卷积层包含不止一个卷积核,并且卷积后的处理跟上面的图像处理过程也有一点点不一样。
我们在上面的博文中,卷积得来的数值进行了平均化。
而在 CNN 中,我们不是将它平均化而是送到一个激活函数里面,得到一个新的输出,激活函数通常有 Sigmoid 和 tanh 函数等,我们以 Sigmoid 为例。
σ ( x ) = 1 1 + e − x \sigma(x)=\frac{1}{1+e^{-x}} σ(x)=1+e−x1
它的函数图形如下:
它有个很好的特性就是,输出值在 0 ~ 1 之间。
def sigmoid(x):
return 1 / (1 + np.exp(-x))
根据公式,可以很简单写出它的实现函数。
所以,我们可以改写
def _con_each(src,kernel):
pixel_count = kernel.size;
pixel_sum = 0;
_src = src.flatten();
_kernel = kernel.flatten();
for i in range(pixel_count):
pixel_sum += _src[i]*_kernel[i];
value = pixel_sum / pixel_count
value = value if value >0 else 0
value = value if value < 255 else 255
value = sigmoid(value)
return value;
到这里,我们完全掌握了如何对一张图片进行卷积操作。
可能有同学会问,如何确定卷积核的大小及它们的值,在传统的图形处理中,卷积核是通过大量开发人员的经验调试出来的,并且它本身具有一定的数学理论支撑,但是在深度学习中,除了核的尺寸是认为设计的,卷积核里面的数值是深度学习自己训练出来的,开发人员在事先是不能确定它的值的,这是它的魅力与神奇之处。
本文示例代码:github_demo
本文内容有扩展和更新,详情请阅读下面的链接内容
【深度学习】多通道图像卷积过程及计算方式
参考
- https://www.zhihu.com/question/22298352
- http://upload.yxtvg.com/kbimg/match-0-1836244055-0



