【深度学习】轻量级神经网络 SqueezeNet 讲解
在深度学习领域,人们一般把注意力集中在如何提高神经网络的准确度上,所以,神经网络的层次越来越深,参数也越来越多,但带来的问题就是神经网络对于硬件的要求越来越高,但在嵌入式硬件上比如手机、自动驾驶的计算平台,这将很吃力,所以,有一些人会将精力放在如何精简和优化网络模型上,以便它们能够比较顺利运行在硬件条件有限的嵌入式设备上面。
而 SqueezeNet 就是一种精简化的轻量级的卷积神经网络结构。
小型 CNN 的优势
- 在分布式平台训练时,如果采用较小的 CNN,意味各个分布式子系统之间通讯量会减少,有助于提高训练性能。
- 未来的自动驾驶汽车都有 OTA,也就是在线升级的功能,较小的 CNN 有助于减少云端的传输压力,因为较小的 CNN 数据量更少,节约了用户下载时间,也节省了流量。
- 较小的 CNN 更容易部署在 FPGA 这样内存受限的硬件上。
SqueezeNet 和 AlexNet 的比较
AlexNet 这一经典的神经网络结构,在深度学习领域是里程碑的象征,后续的 GoogLeNet、VGG、ResNet 等等都是在参考 AlexNet 结构上发展开来的。
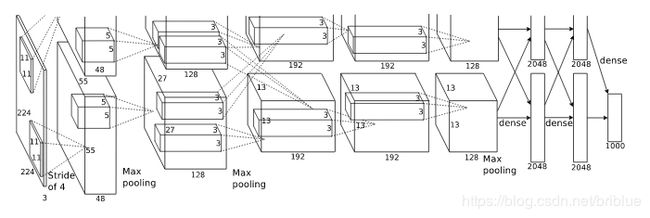
但它有个最大的缺点就是,权重参数实在是太多了,总共有 6 千万个参数。
而 SqueezeNet 的目标就是在保持和 AlexNet 同样的准确度上,参数比它少 50 倍。
CNN 的模块化设计潮流
AlexNet 有 11x11、5x5、3x3 这 3 种卷积核尺寸。
VGG 改革的比较彻底,它全部采用了 3x3 这一尺寸的卷积核。
这样做的原因是 2 个 3x3 的卷积核堆叠后,感受野和 5x5 的卷积核一样,但是参数却更少了。
而和 VGG 同时出现的 GoogLeNet 也有自己的 Inception 结构。
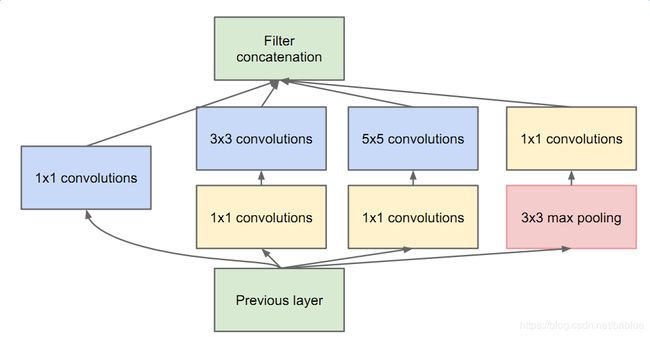
ResNet 深度残差网络,也有自己的残差单元。

这些经典的神经网络都可以看做是普通的卷积层和特殊的卷积模块的堆叠
SqueezeNet 也有自己的卷积模块。
SqueezeNet 的 Fire Module 模块
SqueezeNet 定义了自己的卷积模块,它就是 Fire Module。

SqueezeNet 设计思路有 3 个
- 用 1x1 代替 3x3 的卷积核 当然,这里的替换是不是替换某一层全部的 3x3 卷积核,替换的是大部分。
- 减少 3x3 卷积核的 input 通道数 这个可能有些难以理解,请仔细观察上面结构图中 squeeze 的作用
- 延迟下采样 延迟下采样的好处就是卷积核进行卷积后,可以产生比较大的 Featuremap。
按照这种思路,SqueezeNet 最终设计成为如下形式的结构。

Fire Module 的超参数
我们可以看到,Fire Module 有 1x1、3x3 两种尺寸的卷积核,但是,它们的数量却是超参数,需要认为设定。
Fire Module 分为 squeeze 和 expand 上下两个部分。
squeeze 部分全部又 1x1 卷积核构成,它是上面设计思路第一条的体现,卷积核的数量用 s 1 x 1 s_{1x1} s1x1 表示。
expand 部分又 1x1 和 3x3 的卷积核混合组成,卷积核的数量分别为 e 1 x 1 e_{1x1} e1x1 、 e 3 x 3 e_{3x3} e3x3 。
SqueezeNet 各个权重层,参数数量配置如下。
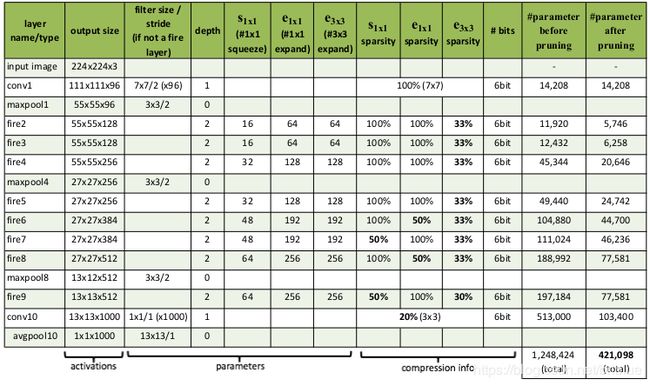
上面的表格显示,SqueezeNet 有 8 个 Fire Module 模块,而每个模块有 3 个超参数,所以它总共有 24 个超参数。
为每一个 fire module 设置参数太麻烦,不够灵活,于是作者决定定制某种规律。
首先定义第一个 fire module 中 expand 卷积核的数量为 b a s e e base_{e} basee。
然后,每经过 f r e q freq freq 个 fire module,后面的 expand 卷积核数量就要增加,要设定一些元参数。
对于第 i 个 fire module 而言,expand 卷积核的数量 e i = b a s e e + i n c r e ∗ [ i f r e q ] e_{i}=base_{e}+incr_{e}*[\frac{i}{freq}] ei=basee+incre∗[freqi]。
但是,expand 卷积核有 1x1 和 3x3 两种,所以需要定义 e i = e i , 1 x 1 + e i , 3 x 3 e_{i}=e_{i,1x1}+e_{i,3x3} ei=ei,1x1+ei,3x3。
3x3 的卷积核数量是 e i , 3 x 3 e_{i,3x3} ei,3x3,它受 p c t 3 x 3 pct_{3x3} pct3x3 控制, e i , 3 x 3 = e i ∗ p c t 3 x 3 e_{i,3x3}=e_{i}*pct_{3x3} ei,3x3=ei∗pct3x3。
所以, e i , 1 x 1 = e i ∗ ( 1 − p c t 3 x 3 ) e_{i,1x1}=e_{i}*(1-pct_{3x3}) ei,1x1=ei∗(1−pct3x3)。
上面讨论的是 firemodule 中 expand 中卷积核的数量定义,那么 squeeze 部分呢?
squeeze 部分只包含 1x1 的卷积核,它的数量由 squeeze ratio(SR) 控制。 s i , 1 x 1 = S R ∗ e i s_{i,1x1}=SR*e_{i} si,1x1=SR∗ei
到这里,SqueezeNet 中 fire module 中的卷积核数量公式全部确定了下来。
SqueezeNet 设定了如下元参数的基准值。
b a s e e = 128 , i n c r e = 2 , p c t s 3 x 3 = 0.5 , f r e q = 2 , S R = 0.125 base_{e} = 128, incr_{e} = 2, pcts_{3x3} = 0.5, freq = 2, SR = 0.125 basee=128,incre=2,pcts3x3=0.5,freq=2,SR=0.125
然后,在这个基础上做元参数的取值变化,发现准确性会有变动。
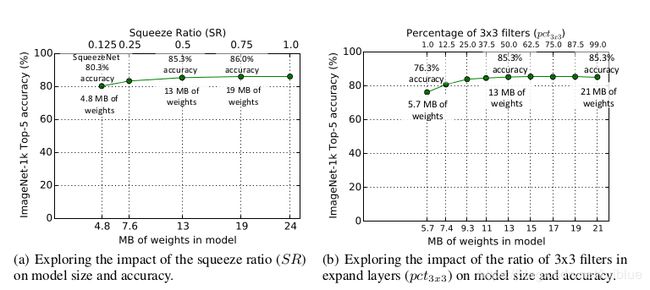
SR 和 pct 变化时,准确率越高,神经网络的参数内存也上去了,怎么选择看开发者自己吧。
SqueezeNet 模块之间的连接实验
前面小节花了大段时间,讲解了 Fire Module ,但它能不能准确运行呢?它们之间的数据怎么流通呢?
为此作者参考 ResNet 的结构,借鉴了 bypass 的思想,设计了 3 个网络对比。
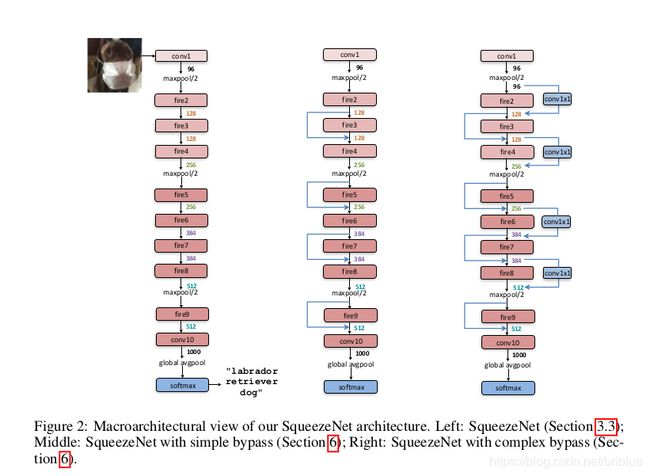
- Valilla SqueezeNet 上图第一个
- Simple bypass 版本,中间的那一个
- Complex bypass 右边的那个。
其实 bypass 就是残差学习的思想。
残差学习可以参考这篇。
以 simple bypass 为例,fire2 的输出+fire3 的输出就是 fire4 的输入。
simple bypass 就是起到 wire 的作用,并且它非常有限制,那就是不是每一个 fire module 都能这样连接,它要求 input 和 output 的通道数量一样。
如果能让每个 fire module 都有这种残差学习功能,就需要引入 complex bypass 机制,如果两个 fire module 用 simple bypass 也没有办法解决 input 和 output 相等的问题,那么就又灵活的 1x1 卷积核的数量做补充。
simple bypass 和 complex bypass 都能提高 SqueezeNet 的变现,但却更复杂了。

SqueezeNet + Simple Bypass 的方案提高了准确率,并且没有增加额外的内存需求。
SqueezeNet 的轻量化体现在哪里?
- 因为大量采用 1x1 和 3x3 所以,相对于 AlexNet 这样的网络,SqueezeNet 本身就小,如果一个参数在内存中是 32bit,那么 AlexNet 不经过压缩的内存是 240MB,而 SqueezeNet 是 4.8 MB。
- SqueezeNet 采用压缩手段 Deep Compression 后效果极佳。
神经网络的压缩手段比较有名的有SVD、Network Pruning、Deep Compression,它们都能大幅度精简神经网络,但是 SqueezeNet 配合 Deep Compression使用却展示出匪夷所思的表现。
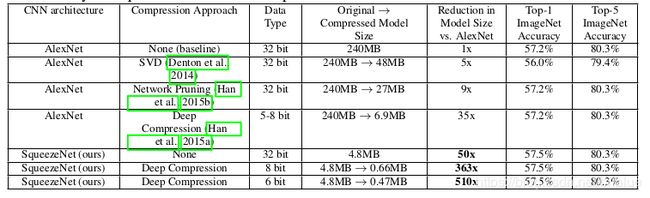
虽然,Deep Compression 使用了量化手段,它让每个参数只有 6~8 bit,但像 0.66MB 大小就能存储一个神经网络,这显然极大鼓舞了人们在嵌入式设备上进行深度学习的探索。