【笔记】计算机的运算方法（二）

三、定点运算

1.移位运算

移位的意义

  二进制表示的机器数在相对于小数点作n位左移或右移时，其实质就是该数乘以或除以 2n 2 n 。当某计算机没有乘除法运算线路时，可以采用移位和加法相结合，实现乘除运算。
  计算机中机器数的字长往往是固定的，当机器数左移n位或右移n位时，必然会使其n位低位或n位高位出现空位。对有符号数的移位称为算数移位。

算术移位规则

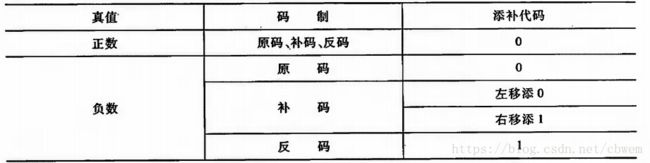
  对于正数，由于 [x]原=[x]补=[x]反= [ x ] 原 = [ x ] 补 = [ x ] 反 = 真值，故移位后出现的空位均以0添之。对于负数，由于原码、补码和反码的表示形式不同，故当机器数移位时，对其空位的填补规则也不同。
  不论是整数还是负数，移位后其符号位均不变。

• 机器数为正时，不论是左移还是右移，添补的代码均为0.
• 由于负数的原码数值部分与真值相同，故在移位时只要使符号位不变，其空位均添0即可。
• 由于负数的反码各位除符号位外与负数的原码正好相反，故移位后所舔代码应与原码相反，即全部添1。
• 负数的补码左移时，因空位出现在低位，则添补的代码与原码相同，即添0；右移时因空位出现在高位，则填补的代码应与反码相同，即添1。

  对于正数，三种机器数移位后符号位均不变，左移时最高数位丢1，结果出错；右移时最低数位丢1，影响精度。
  对于负数，三种机器数算术移位后符号位均不变。负数的原码左移时，高位丢1，结果出错；右移时，低位丢1，影响精度。负数的补码左移时，高位丢0，结果出错；右移时，低位丢1，影响精度。负数的反码左移时，高位丢0，结果出错；右移时，低位丢0，影响精度。

算术移位和逻辑移位的区别

  有符号数的移位称为算数移位，无符号数的移位称为逻辑移位。逻辑移位的规则是：逻辑左移时，高位移丢，低位添0；逻辑右移时，低位移丢，高位添0。为了避免算术左移时最高数位丢1，可采用带进位（ Cy C y ）的移位。算术左移时，符号位移至 Cy C y ，最高数位就可避免移丢。

2.加法与减法运算

补码加法运算的基本公式

  补码加法的基本公式如下：
  整数   [A]补+[B]补=[A+B]补（mod 2n+1） [ A ] 补 + [ B ] 补 = [ A + B ] 补 （ m o d   2 n + 1 ）
  小数   [A]补+[B]补=[A+B]补（mod 2） [ A ] 补 + [ B ] 补 = [ A + B ] 补 （ m o d   2 ）

  即补码表示的两个数在进行加法运算时，可以把符号位与数值等同处理，只要结果不超出机器能表示的数值范围，运算后的结果按 2n+1 2 n + 1 取模（对于整数）或按 2 2 取模（对于小数），就能得到本次加法的运算结果。

  补码减法的基本公式如下：
  整数   [A−B]补=[A]补+[−B]补（mod 2n+1） [ A − B ] 补 = [ A ] 补 + [ − B ] 补 （ m o d   2 n + 1 ）
  小数   [A−B]补=[A]补+[−B]补（mod 2） [ A − B ] 补 = [ A ] 补 + [ − B ] 补 （ m o d   2 ）

  而 [−B]补 [ − B ] 补 由 [B]补 [ B ] 补 连同符号位在内，每位取反，末位加1而得。

  不论操作数是正还是负，在做补码加减法时，只需将符号位和数值部分一起参加运算，并且将符号位产生的进位自然丢掉即可。
  这种超出机器字长的现象叫溢出。为此，在补码定点加减运算过程中，必须对结果是否溢出做出明确的判断。

溢出判断

  （1）用一位符号位判断溢出
  对于加法，只有在正数加正数和负数加负数两种情况下才可能出现溢出，符号位不同的两个数相加是不会溢出的。
  对于减法，只有在正数减负数或负数减正数两种情况下才可能出现溢出，符号位相同的两个数相减是不会溢出的。

  只要实际参加操作的两个数符号相同，结果又与原操作数的符号不同，即为溢出。
  计算机中采用1位符号位判断时，为了节省时间，通常用符号位产生的进位与最高位有效位产生的进位异或操作后，按其结果进行判断。若异或结果为1，即为溢出；异或结果为0，则无溢出。

  （2）用两位符号位判断溢出
  2为符号位的补码，即变形补码，它是以4为模的，其定义为

[x]补′={x,4+x,1>x≥00>x≥−1  (mod 4) [ x ] 补 ′ = { x , 1 > x ≥ 0 4 + x , 0 > x ≥ − 1     ( m o d   4 )

  在用变形补码作加法时，2位符号位要连同数值部分一起参加运算，而且高位符号位产生的进位自动丢失，便可得正确结果，即

[x]补′+[y]补′=[x+y]补′  (mod 4) [ x ] 补 ′ + [ y ] 补 ′ = [ x + y ] 补 ′     ( m o d   4 )

  变形补码判断溢出的原则是： 当2位符号位不同时，表示溢出，否则无溢出。不论是否发生溢出，高位（第1位）符号位永远代表真正的符号。
  符号位为“01”，表示溢出，又因第1位符号位为“0”，表示结果的真正符号为正，故“01”表示 正溢出。
  符号位为“10”，表示溢出，又因第1位符号位为“1”，表示结果的真正符号为负，故“10”表示 负溢出。
  上述结论对于整数也同样适用。在浮点机中，当阶码用两位符号位表示时，判断溢出的原则与小数的完全相同。
  采用双符号位方案时，寄存器或主存中的操作数只需保存一位符号位即可。因为任何正确的数，两个符号位的值总是相同的，而双符号位在加法器中又是必要的，故在相加时，寄存器中一位符号的值要同时送到加法器的两位符号位的输入端。

补码定点加减法所需的硬件配置

  其中A存放被加数（或被减数）的补码，X存放加数（或减数）的补码。当作减法时，由“求补控制逻辑”将 X¯¯¯¯ X ¯ 送至加法器，并将加法器的最末位外来进位为1，以达到对减数求补的目的。运算结果溢出时，通过溢出判断电路置“1”溢出标记V。 GA G A 为加法标记， GS G S 为减法标记。

补码加减运算控制流程

3.乘法运算

笔算乘法的改进

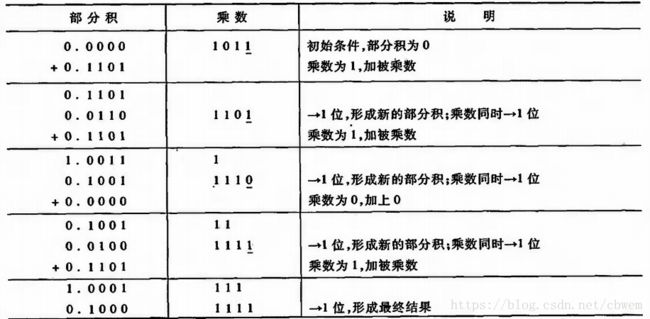
  两数相乘的过程，可视为加法和移位两种运算。

  例：设A=0.1101，B=0.1011，求 A×B A × B 。

  运算规则如下：

• 乘法运算可用移位和加法来实现，两个4位数相乘，总共需要4次加法运算和4次移位。
• 由乘数的末尾值确定被乘数是否与原部分积相加，然后右移一位，形成新的部分积；同时乘数也右移一位，由次低位作为新的末位，空出最高位放部分积的最低位。
• 每次作加法时，被乘数仅仅与原部分积的高位相加，其低位被移至成乘数所空出的高位位置。

  用一个寄存器存放被乘数，一个寄存器存放乘积的高位，另一个寄存器存放乘数及乘积的低位，再配上加法器及其他相应电路，就可组成乘法器。又因加法志在部分积的高位进行，故不但节省了器材，而且还缩短了运算时间。

原码乘法

  上述讨论结果可直接用于原码一位乘，只需加上符号位处理即可。

（1）原码一位乘运算规则

  以小数为例：
  设   [x]原=x0.x1x2…xn [ x ] 原 = x 0 . x 1 x 2 … x n
      [y]原=y0.y1y2…yn [ y ] 原 = y 0 . y 1 y 2 … y n
  则 [x]原⋅[y]原=x0⊕y0.(0.x1x2…xn)(0.y1y2…yn) [ x ] 原 ⋅ [ y ] 原 = x 0 ⊕ y 0 . ( 0. x 1 x 2 … x n ) ( 0. y 1 y 2 … y n )
  式中， 0.x1x2…xn 0. x 1 x 2 … x n 为x的绝对值，记作 x∗ x ∗ ;； 0.y1y2…yn 0. y 1 y 2 … y n 为y的绝对值，记作 y∗ y ∗ 。

  原码一位乘运算规则：

• 乘积的符号位由两原码符号位异或运算结果决定。
• 乘积的数值部分由两数绝对值相乘，其通式为：
  x∗⋅y∗=2−1(y1x∗+(…+2−1(yn−1x∗+2−1(ynx∗+0))…)) x ∗ ⋅ y ∗ = 2 − 1 ( y 1 x ∗ + ( … + 2 − 1 ( y n − 1 x ∗ + 2 − 1 ( y n x ∗ + 0 ) ) … ) )

  例：已知x=-0.1110，y=-0.1101，求 [x⋅y]原 [ x ⋅ y ] 原 。

  故 [x⋅y]原=0.10110110 [ x ⋅ y ] 原 = 0.10110110

  注：这里部分积取n+1位，以便存放乘法过程中绝对值大于或等于1的值。此外，由于乘积的数值部分是两数绝对值相乘的结果，故原码一位乘法运算过程中的右移操作均为逻辑右移。

（2）原码一位乘运所需的硬件配置

  A、X、Q均为n+1位的寄存器，其中X存放被乘数的原码，Q存放乘数的原码。移位和加控制电路受末尾乘数 Qn Q n 的控制（当 Qn=1 Q n = 1 时，A和X内容相加后，A、Q右移移位；当 Qn=0 Q n = 0 时，只作A、Q右移一位的操作）。计数器C用于控制逐位相乘的次数。S存放乘积的符号。 GM G M 为乘法标记。

（3）原码一位乘控制流程

  为了提高乘法速度，可采用原码两位乘。

（4）原码两位乘
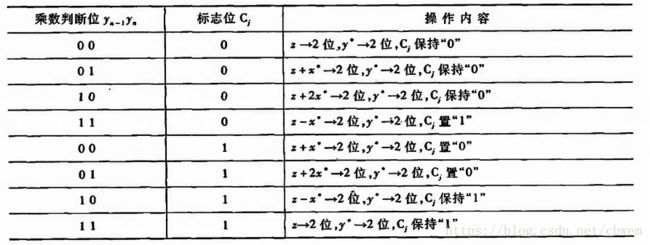
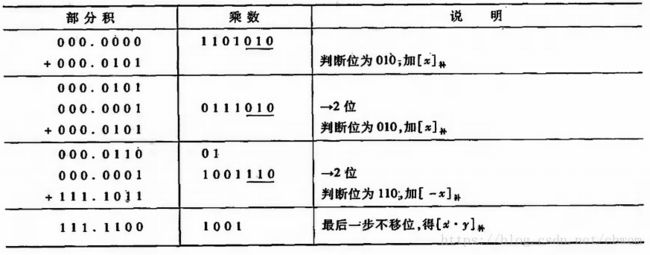
  原码两位乘是用两位乘数的状态来决定新的部分积如何形成，因此可提高运算速度。

  表中3倍被乘数的获得较难。此刻可将3视为4-1，即把乘以3分两步完成：第一步先完成减1倍被乘数的操作，第二步完成加4倍被乘数的操作。而加4倍被乘数的操作实际上是由比“11”高的两位乘数代替完成的，可看作是在高两位乘数上加“1”。这个“1”暂存在 Ci C i 触发器中。机器完成 Ci C i 置“1”，即意味着对高两位乘数加1，也即要求高两位乘数代替本两位乘数“11”来完成加4倍被乘数的操作。

  表中z表示原有部分积， x∗ x ∗ 表示被乘数的绝对值， y∗ y ∗ 表示乘数的绝对值，当进行 −x∗ − x ∗ 运算时，一般都采用加 [−x∗]补 [ − x ∗ ] 补 来实现。

  为了统一用两位乘数和一位 Ci C i 共同配合管理全部操作，与原码一位乘不同的是，需在乘数（当乘数位数为偶数时）的最高位前增加两个0。当乘数最高两个有效位出现“11”时，需将 Cj C j 置为“1”，再与所添补的两个0结合呈001状态，以完成加 x∗ x ∗ 的操作*（此步不必移位）。

  例：设x=0.111111，y=-0.111001，用原码两位乘求 [x⋅y]原 [ x ⋅ y ] 原 。

  故 [x⋅y]原=1.111000000111 [ x ⋅ y ] 原 = 1.111000000111

  注：当乘数为偶数时，需要做n/2次移位，最多做n/2+1次加法。当乘数为奇数时，乘数高位前可只增加一个"0"，此时需做n/2+1次移位（最后一步移一位），最多需做n/2+1次加法。

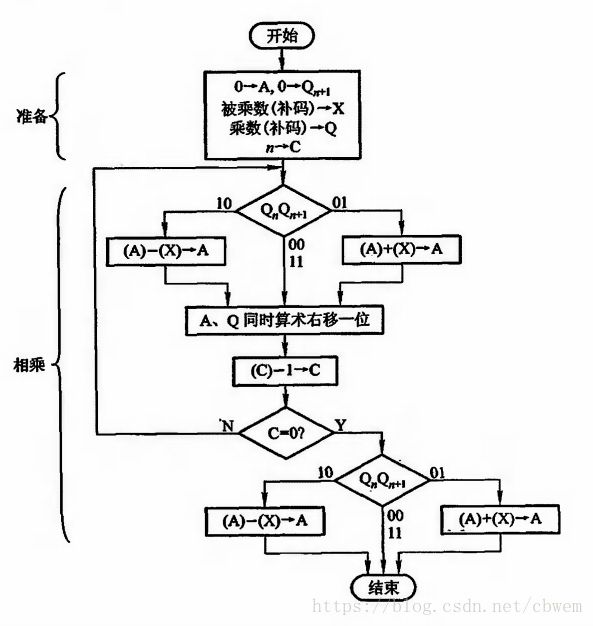
补码乘法

（1）补码一位乘运算规则
  设   [x]补=x0.x1x2…xn [ x ] 补 = x 0 . x 1 x 2 … x n
      [y]补=y0.y1y2…yn [ y ] 补 = y 0 . y 1 y 2 … y n

  1）被乘数x符号任意，乘数y符号为正

  则 [x⋅y]补=[x]补⋅[y]补=[x]补⋅y [ x ⋅ y ] 补 = [ x ] 补 ⋅ [ y ] 补 = [ x ] 补 ⋅ y
  当乘数y为正数时，不管被乘数x符号如何，都可按原码乘法的规则运算。

  2）被乘数x符号任意，乘数y符号为负
  则 [x⋅y]补=[x]补(0.y1y2…yn)+[−x]补 [ x ⋅ y ] 补 = [ x ] 补 ( 0. y 1 y 2 … y n ) + [ − x ] 补
  当乘数为负时是把乘数的补码 [y]补 [ y ] 补 去掉符号位，当成一个正数与 [x]补 [ x ] 补 相乘，然后加上 [−x]补 [ − x ] 补 进行校正，也称校正法。

  例：已知 [x]补=1.0101 [ x ] 补 = 1.0101 ， [y]补=0.1101 [ y ] 补 = 0.1101 ，求 [x⋅y]补 [ x ⋅ y ] 补 。

  故乘积 [x⋅y]补=1.01110001 [ x ⋅ y ] 补 = 1.01110001 。

  校正法与乘数的符号有关，虽然可将乘数和被乘数互换，使乘数保持正，不必校正，但当两数均为负时必须校正。实现校正法的控制线路比较复杂。若不考虑操作数的符号，用统一的规则进行运算可采用比较法。

  3）被乘数x和乘数y符号均为任意
  比较法又称Booth算法。

  设   [x]补=x0.x1x2…xn [ x ] 补 = x 0 . x 1 x 2 … x n
      [y]补=y0.y1y2…yn [ y ] 补 = y 0 . y 1 y 2 … y n
  则 [x⋅y]补=[x]补(0.y1y2…yn)−[x]补⋅y0 [ x ⋅ y ] 补 = [ x ] 补 ( 0. y 1 y 2 … y n ) − [ x ] 补 ⋅ y 0

  在mod 2的前提下， [−x]补=−[x]补 [ − x ] 补 = − [ x ] 补 成立。
  则 [x⋅y]补=[x]补(y12−1+y22−2+…+yn2−n−[x]补⋅y0) [ x ⋅ y ] 补 = [ x ] 补 ( y 1 2 − 1 + y 2 2 − 2 + … + y n 2 − n − [ x ] 补 ⋅ y 0 )
        =[x]补[(y1−y0)+(y2−y1)2−1+…+(yn+1−yn)2−n] = [ x ] 补 [ ( y 1 − y 0 ) + ( y 2 − y 1 ) 2 − 1 + … + ( y n + 1 − y n ) 2 − n ]
  其中 yn+1=0 y n + 1 = 0 。

  开始时 yn+1=0 y n + 1 = 0 ，部分积初值 [z0]补 [ z 0 ] 补 为0，每一步乘法由 (yi+1−yi) ( y i + 1 − y i ) （i=1,2,…，n）决定原部分积加 [x]补 [ x ] 补 或加 [−x]补 [ − x ] 补 或加0，再右移一位得新的部分积，以此重复n步。第n+1步由 (y1−y0) ( y 1 − y 0 ) 决定原部分积加 [x]补 [ x ] 补 或加 [−x]补 [ − x ] 补 或加0，但不移位，即得 [x⋅y]补 [ x ⋅ y ] 补 。

  例：已知 [x]补=0.1101 [ x ] 补 = 0.1101 ， [y]补=0.1011 [ y ] 补 = 0.1011 ，求 [x⋅y]补 [ x ⋅ y ] 补 。

  故 [x⋅y]补=0.10001111 [ x ⋅ y ] 补 = 0.10001111 。

  Booth算法的部分积仍取双符号位，乘数因符号位参加运算，故多取1位。

（2）补码比较法（Booth算法）所需的硬件配置

  A、X、Q均为n+2位寄存器，其中X存放被乘数的补码（含两位符号位），Q存放乘数的补码（含最高1位符号位和最末1位附加位），移位和加控制逻辑受Q寄存器末2位乘数控制。计数器C用于控制逐位相乘的次数， GM G M 为乘法标记。

（3）补码比较法（Booth算法）控制流程

  为了提高乘法的运算速度，可采用补码两位乘。

（4）补码两位乘
  补码两位乘运算规则是根据补码一位乘的规则，把比较 ynyn+1 y n y n + 1 的状态应执行的操作和比较 yn−1yn y n − 1 y n 的状态应执行的操作合并成一步得出的。

  操作数中出现加 2[x]补 2 [ x ] 补 和加 2[−x]补 2 [ − x ] 补 ，故除右移两位的操作外，还有被乘数左移一位的操作；而加 2[x]补 2 [ x ] 补 和加 2[−x]补 2 [ − x ] 补 都可能因溢出而侵占双符号位，故部分积和被乘数采用3为符号位。

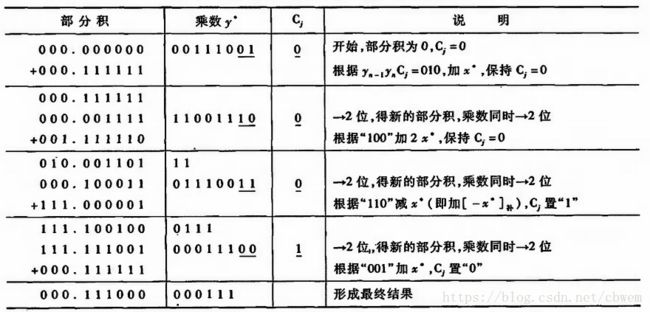
  例：已知 [x]补=0.0101 [ x ] 补 = 0.0101 ， [y]补=1.0101 [ y ] 补 = 1.0101 ，求 [x⋅y]补 [ x ⋅ y ] 补 。

  故 [x⋅y]补=1.11001001 [ x ⋅ y ] 补 = 1.11001001 。
  与补码一位乘相比，补码两位乘的部分积多取1为符号位（共3位），乘数也多取1为符号位（共2位），这是由于乘数每次右移2位，且用3位判断，故采用双符号位更便于硬件实现。当乘数数值位为偶数时，乘数取2位符号位，共需作n/2次移位，最多作n/2+1次加法，最后一步不移位；当n为奇数时，可补0变为偶数位，以简化逻辑操作。也可对乘数取1位符号位，此时共进行n/2+1次加法运算和n/2+1次移位（最后一步移一位）。

4.除法运算

分析笔算除法

  特点可归纳如下：

• 每次上商都是由心算来比较余数（被除数）和除数的大小，确定商为“1”还是为“0”。
• 每做一次减法，总是保持余数不懂，低位补0，再减去右移后的除数。
• 上商的位置不固定。
• 商符单独处理。

  上述规则若照搬到计算机里实现有一定困难：

• 机器不能“心算”上商，必须通过比较被除数（或余数）和除数绝对值大小来确定商值。
• 按照每次减法总是保持余数不懂低位补0，再减去右移后的除数这一规则，在要求加法器的位数必须为除数的两倍。
• 笔算求商时是从高位向低位逐位求的，而要求机器把每位商直接写到寄存器的不同位置也是不可取的。

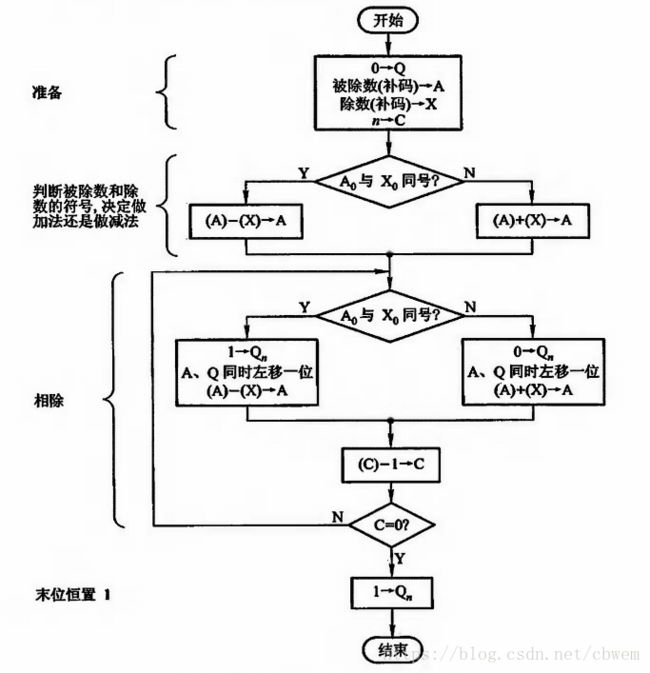
原码除法

  小数定点除法对被除数和除数有一定的约束，即必须满足下列条件：

0<|被除数|≤|除数| 0 < | 被 除 数 | ≤ | 除 数 |

  实现除法运算时，还应避免除数为0或被除数为0。
  原码除法中由于对余数的处理不同，又可分为 恢复余数法和 不恢复余数法（加减交替法）两种。

（1）恢复余数法
  特点是：当余数为负时，需加上除数，将其恢复成原来的余数。

  例：已知 x=−0.1011 x = − 0.1011 ， y=−0.1101 y = − 0.1101 ，求 [xy]原 [ x y ] 原 。

  故商值为0.1101，商的符号位为 x0⊕y0=1⊕1=0 x 0 ⊕ y 0 = 1 ⊕ 1 = 0 ，故 [xy]原=0.1101 [ x y ] 原 = 0.1101 。

  第一次上的商在商的整数位上，这对小数除法而言，可用它作溢出判断。即当该位为“1”时，表示此除法溢出，不能进行，应由程序进行处理；当该位为“0”时，说明除法合法，可以进行。
  在恢复余数法中，每当余数为负时，都需恢复余数，这就延长了机器出发的时间，操作也很不规则，对线路结构不利。加减交替法可克服这些缺点。

（2）加减交替法
  加减交替法又称为不恢复余数法，可以认为它是恢复余数法的一种改进算法。
  分析原码恢复余数法得知：

• 当余数 Ri>0 R i > 0 时，可上商“1”，再对 Ri R i 左移一位后减除数，即 2Ri−y∗ 2 R i − y ∗ 。
• 当余数 Ri<0 R i < 0 时，可上商“0”，然后先做 Ri+y∗ R i + y ∗ ，即完成恢复余数的运算，再做 2(Ri+y∗)−y∗ 2 ( R i + y ∗ ) − y ∗ ，即 2Ri+y∗ 2 R i + y ∗ 。

  故原码恢复余数法可归纳为：

• 当 Ri>0 R i > 0 时，上商“1”，做 2Ri−y∗ 2 R i − y ∗ 的运算。
• 当 Ri<0 R i < 0 时，上商“0”，做 2Ri+y∗ 2 R i + y ∗ 的运算。

  例：已知 x=−0.1011 x = − 0.1011 ， y=−0.1101 y = − 0.1101 ，求 [xy]原 [ x y ] 原 。

  故商值为0.1101，商的符号位为 x0⊕y0=1⊕0=1 x 0 ⊕ y 0 = 1 ⊕ 0 = 1 ，故 [xy]原=1.1101 [ x y ] 原 = 1.1101 。

  倘若比例因子选择合恰当，出发结果不溢出，则第一次商肯定是0.如果省去这位商，只需上商n次即可，此时除法运算一开始应将被除数左移一位减去除数，然后再根据余数上商。
  操作数也可采用双符号位，此时移位操作可按算术左移处理最高符号位是真正的符号，次高位符号位在移位时被第一数值位占用。

（3）原码加减交替法所需的硬件配置

  A、X、Q均为n+1位寄存器，其中A存放被除数的原码，X存放除数的原码。移位和加控制逻辑受Q的末位 Qn Q n ( Qn=1 Q n = 1 作减法， Qn=0 Q n = 0 作加法)，计数器C用于控制逐位相除的次数n， GD G D 为除法标记，V为溢出标记，S为商符。

（4）原码加减交替法控制流程

  对于整数除法，要求满足以下条件：

0<|除数|≤|被除数| 0 < | 除 数 | ≤ | 被 除 数 |

  因为这样才能得到整数商。通常在做整数除法前，先要对这个条件进行判断，若不满足上述条件，机器发出出错信号，程序要重新设定比例因子。
  小数除法完全适用于整数除法，只是整数除法的被除数位数可以是除数的两倍，且要求被除数的高n位要比除数（n位）小，否则即为溢出。如果被除数和除数的位数都是单字长，则要在被除数前面加上一个字的0，从而扩展成双倍字长在进行运算。
  为了提高除法速度，可采用阵列除法器。

补码除法

（1）补码加减交替法运算规则

  补码除法的符号位和数值部分是一起参加运算的。
1.欲确定商值，必须先比较被除数和除数的大小，然后才能求得商值。
  比较被除数和除数的大小

• 当被除数与除数同号时，做减法，若得到的余数与除数同号，表示“够减”，否则表示“不够减”。
• 当被除数与除数异号时，做加法，若得到的余数与除数同号，表示“够减”，否则表示“不够减”。

  商值的确定

• 如果 [x]补 [ x ] 补 与 [y]补 [ y ] 补 同号，商为正，则“够减”时上商“1”，“不够减”时上商“0”。
• 如果 [x]补 [ x ] 补 与 [y]补 [ y ] 补 异号，商为负，则“够减”时上商“0”，“不够减”时上商“1”。

2.在补码除法中，商符是在求商的过程中自动形成的。
  在小数定点除法中，被除数的绝对值必须小于除数的绝对值，否则商大于1而溢出。当 [x]补 [ x ] 补 与 [y]补 [ y ] 补 同号时， [x]补−[y]补 [ x ] 补 − [ y ] 补 所得的余数 [R0]补 [ R 0 ] 补 必与 [y]补 [ y ] 补 异号，上商“0”，恰好与商的符号一致；当 [x]补 [ x ] 补 与 [y]补 [ y ] 补 异号时， [x]补+[y]补 [ x ] 补 + [ y ] 补 所得的余数 [R0]补 [ R 0 ] 补 必与 [y]补 [ y ] 补 同号，上商“1”，这也与商的符号一致。
  商的符号还可用来判断商是否溢出。当 [x]补 [ x ] 补 与 [y]补 [ y ] 补 同号时，若 [R0]补 [ R 0 ] 补 与 [y]补 [ y ] 补 同号，上商“1”，即溢出。当 [x]补 [ x ] 补 与 [y]补 [ y ] 补 异号时，若 [R0]补 [ R 0 ] 补 与 [y]补 [ y ] 补 异号，上商“0”，即溢出。
  对于小数补码运算，商等于“-1”应该是允许的，但这需要特殊处理。

3.新余数 [Ri+1]补 [ R i + 1 ] 补 的获得方法与原码加减交替法极相似
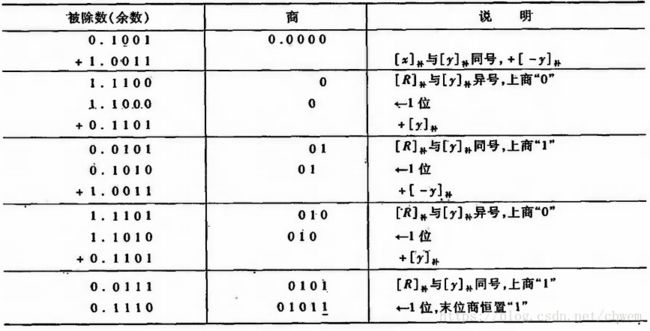
  其算法规则为：

• 当 [Ri]补 [ R i ] 补 与 [y]补 [ y ] 补 同号时，上商“1”，新余数
  [Ri+1]补=2[Ri]补−[y]补=2[Ri]补+[−y]补 [ R i + 1 ] 补 = 2 [ R i ] 补 − [ y ] 补 = 2 [ R i ] 补 + [ − y ] 补
• 当 [Ri]补 [ R i ] 补 与 [y]补 [ y ] 补 异号时，上商“0”，新余数
  [Ri+1]补=2[Ri]补+[y]补 [ R i + 1 ] 补 = 2 [ R i ] 补 + [ y ] 补

  如果对商的精度没有特殊要求，一般可采用“末位恒置1”法，这种方法操作简单，易于实现，而且最大误差仅为 2−n 2 − n 。

  例：已知 x=0.1001 x = 0.1001 ， y=0.1101 y = 0.1101 ，求 [xy]补 [ x y ] 补 。

所以 [xy]补 [ x y ] 补 =0.1011。

  可见n位小数补码除法共上商n+1次（末位恒置“1”），第一次可用来判断是否溢出。共移位n次，并用移位次数判断除法是否结束。

（2）补码加减交替法所需的硬件配置
  硬件配置基本上与原码的相似，但S触发器可以省掉，因为补码除法的商符在运算中自动形成。此外在寄存器中存放的均为补码。

（3）补码加减交替法的控制流程

  补充说明：

• 图中未画出补码除法溢出判断的内容。
• 多做一次加（或减）法，其实z 末位恒置“1”前，只需移位而不必做加（或减）法。
• 与原码除法一样，图中均未指出对0的检测。
• 为了节省时间，上商和移位操作可以同时进行。