计算几何学习笔记之点和直线

向量的基本运算http://blog.csdn.net/cqbzwja/article/details/51030712
直线用参数方程表示，参数方程就是直线上任意一点，加上一个方向向量，以及参数t。假设直线上所有点满足 P=P0+tv⃗  ，那么t为参数，P0是直线上任意一点，v是直线的方向。假设点Q有 Q=P0+t0v⃗  ，则表示Q在P0点的v方向的t倍|v|的位置，特别地当 |v⃗ |=1 时有 |P0Q|=t 。
当直线为射线的时候 t>0 ，直线 t∈R ,线段 t∈[0,1]
直线交点：设直线分别为 l1:P+tv,l2:Q+tw ，交点在第一条直线上的参数为t1，第二条直线上的参数为t2，定义 u⃗ =P−Q 有：

t1=cross(w,u)cross(v,w),t2=cross(v,u)cross(v,w)

证明如下：

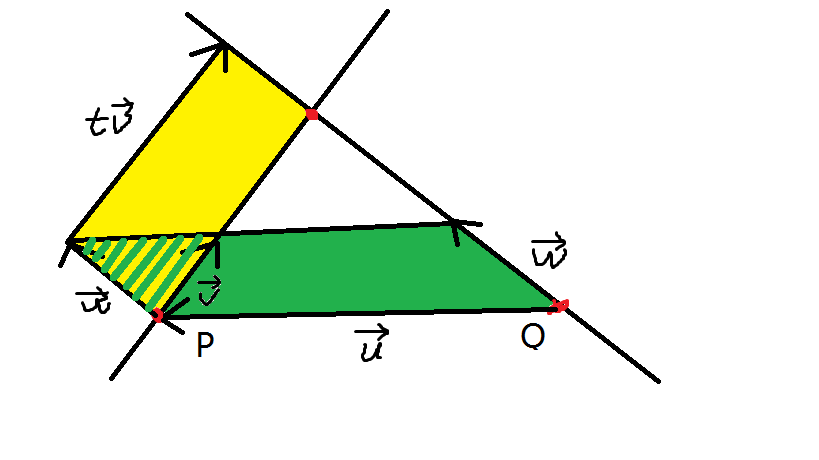
不难得到 Syellow=Sgreen ，则有 tv⃗ ∗w⃗ =w⃗ ∗u⃗ ⇒t=w⃗ ∗u⃗ v⃗ ∗w⃗ 
代码：

poi GetLineIntersection(poi P,vec v,poi Q,vec w)
{
    double t = cross(w, P-Q) /cross(v, w);
    return P+v*t;
}

点到直线距离：叉积为平行四边形面积，那么用面积除以底边就得到了距离。

double DistanceToLine(poi p,poi A,poi B)
{
    vec v1 = B-A, v2 = p-A;
    return fabs(cross(v1,v2)) /length(v1);
}

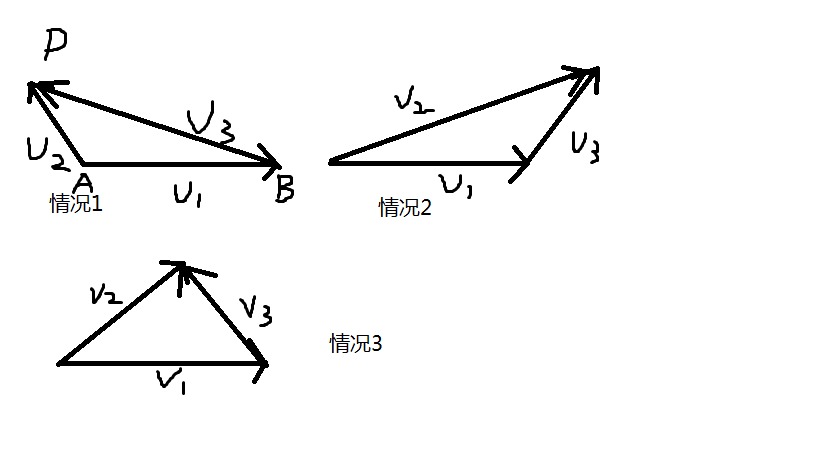
点到线段的距离：有可能是P到直线AB的距离，也可能是到A点的距离，也可能是到点B的距离。代码：

double DistanceToSegment(poi p,poi A,poi B)//点p到线段AB的距离
{
    if(A == B) return length(p-A);
    vec v1 = B-A, v2 = p-A, v3 = p-B;
    if(dcmp(dot(v1,v2)) < 0) return length(v2);
    else if(dcmp(dot(v1,v3)) > 0) return length(v3);
    else return fabs(cross(v1,v2)) /length(v1);
}

点在直线上的投影：设点P在直线AB上的投影点为Q，AB为A+tv(v是向量AB)。设点Q的坐标为 Q=A+t0v。两个相互垂直的向量的点乘值为0，可以得到：
v⃗ ⋅P−(A+t0v)⇒v⃗ ⋅AP→−t0∗(v⃗ ⋅v⃗ )

poi GetLineProjection(poi p,poi A,poi B)
{
    return A + (B-A)*(dot(B-A,P-A) /dot(B-A,B-A));
}

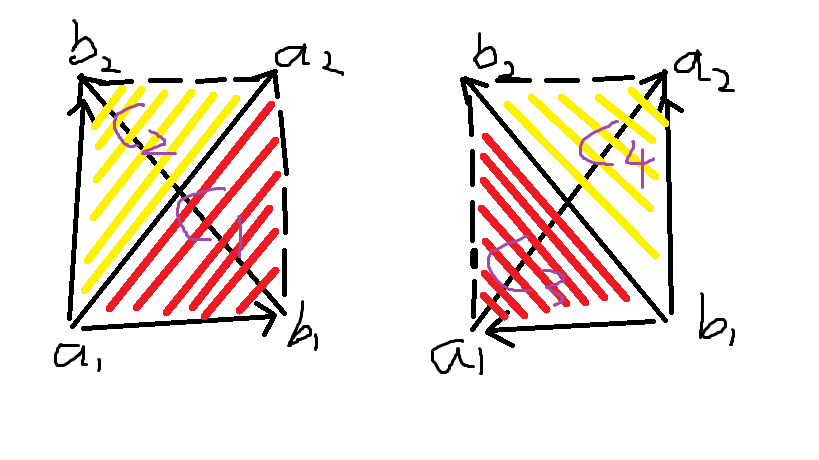
线段相交判定(不含端点)：两条线段相交的充分必要条件是：每条线段的两个端点都在另外一条线段的两侧（叉积符号不同）

bool SegmentProperIntersection(poi a1,poi a2,poi b1,poi b2)
{
    double c1 = cross(a2-a1, b1-a1), c2 = cross(a2-a1, b2-a1), c3 = cross(b2-b1, a1-b1), c4 = cross(b2-b1, a2-b1);
    return dcmp(c1)*dcmp(c2) < 0&&dcmp(c3)*dcmp(c4) < 0;  
}