二叉树的非递归遍历:Java语言实现
1 前言
上一篇写了《二叉树的递归遍历:Java语言实现》,现在用java实现下二叉树的非递归遍历。
2 二叉树的非递归遍历
根据前序遍历访问的顺序,优先访问根结点,然后再分别访问左孩子和右孩子。即对于任一结点,其可看做是根结点,因此可以直接访问。访问完之后,若其左孩子不为空,按相同规则访问它的左子树;当访问其左子树时,再访问它的右子树。因此其处理过程如下:
对于任一结点P:
1)将结点P入栈,并访问结点P;
2)判断结点P的左孩子是否为空,若为空,则取栈顶结点并进行出栈操作,并将栈顶结点的右孩子置为当前的结点P,循环至1);若不为空,则将P的左孩子置为当前的结点P;
3)直到P为NULL并且栈为空,则遍历结束。
//先序遍历:非递归方法
public void PreOrderIterative(BinaryTreeNode root) {
BinaryTreeNode temp = root;
Stack s = new Stack();
while (temp != null || !s.isEmpty()) {
while (temp != null) { //遇到一个结点,就把它压栈并访问它,然后去遍历它的左子树;
s.push(temp);
System.out.print(temp.getData() + " ");
temp = temp.getLeft();
}
if(!s.isEmpty()) {
temp = s.pop();//当左子树遍历结束后,从栈顶弹出这个结点;
temp = temp.getRight();//然后按其右指针再去先序遍历该结点的右子树
}
}
} 2.2 中序遍历
根据中序遍历的顺序,对于任一结点,优先访问其左孩子,而左孩子结点又可以看做一根结点,然后继续访问其左孩子结点,直到遇到左孩子结点为空的结点才进行访问,然后按相同的规则访问其右子树。因此其处理过程如下:
对于任一结点P,
1)若其左孩子不为空,则将P入栈并将P的左孩子置为当前的P,然后对当前结点P再进行相同的处理;
2)若其左孩子为空,则取栈顶元素并进行出栈操作,访问该栈顶结点,然后将当前的P置为栈顶结点的右孩子;
3)直到P为NULL并且栈为空则遍历结束
//中序遍历:非递归方法
public void InOrderIterative(BinaryTreeNode root) {
BinaryTreeNode temp = root;
Stack s = new Stack();
while (temp != null || !s.isEmpty()) {
while (temp != null) { //遇到一个结点,就把它压栈,并去遍历它的左子树;
s.push(temp);
temp = temp.getLeft();
}
if(!s.isEmpty()) {
temp = s.pop();//当左子树遍历结束后,从栈顶弹出这个结点并访问它;
System.out.print(temp.getData() + " ");
temp = temp.getRight();// 然后按其右指针再去中序遍历该结点的右子树
}
}
} 2.3 后序遍历
首先要搞清楚先序、中序、后序的非递归算法共同之处:用栈来保存先前走过的路径,以便可以在访问完子树后,可以利用栈中的信息,回退到当前节点的双亲节点,进行下一步操作。
后序遍历的非递归算法是三种顺序中最复杂的,原因在于,后序遍历是先访问左、右子树,再访问根节点,而在非递归算法中,利用栈回退到时,并不知道是从左子树回退到根节点,还是从右子树回退到根节点,如果从左子树回退到根节点,此时就应该去访问右子树,而如果从右子树回退到根节点,此时就应该访问根节点。所以相比前序和后序,必须得在压栈时添加信息,以便在退栈时可以知道是从左子树返回,还是从右子树返回进而决定下一步的操作。
这里采取的做法为:引入一个pre指针,标记访问当前节点的之前访问的节点。如果root.right为pre,或者root.right为null,则可以判断已经从右子树访问返回。
//后序遍历:非递归方法
public void PostOrderIterative(BinaryTreeNode root) {
BinaryTreeNode temp = root;
BinaryTreeNode pre = null;//标记访问序列中前一个二叉树节点(当前节点的之前访问的节点)
Stack s = new Stack();
while (temp != null || !s.isEmpty()) {
while (temp != null) {
s.push(temp);
temp = temp.getLeft();
}
if(!s.isEmpty()) {
temp = s.peek();
//如果一个节点右孩子是空,或者右孩子刚被访问过,那么就访问该节点。否则就往右孩子走。
if(temp.getRight() == null || temp.getRight() == pre) {
System.out.print(temp.getData() + " ");
s.pop();
pre = temp;
temp = null;
}else {
temp = temp.getRight();
}
}
}
} 2.4 层序遍历
层序遍历的基本过程:
1. 先根节点入队
2. 队列不为空,从队列中取出一个元素
3. 访问该元素所指的结点
4. 若该元素所指结点的左、右孩子结点非空,则将其左、右孩子顺序入队
//层序遍历
public void LevelOrder(BinaryTreeNode root) {
BinaryTreeNode temp;
Queue q = new LinkedList();
if(root == null)
return;
q.add(root);
while (!q.isEmpty()) {
temp = q.poll();//移除并返问队列头部的元素
System.out.print(temp.getData() + " ");
if (temp.getLeft() != null) {
q.add(temp.getLeft());//左孩子入队
}
if (temp.getRight() != null) {
q.add(temp.getRight());//右孩子入队
}
}
} 3 整体代码实现
3.1 建立二叉树结点类
package Binary_Tree_Study;
/**
* Created by Administrator on 2018/5/19.
*/
public class BinaryTreeNode {
private int data;//结点的数据
private BinaryTreeNode left;//指向左孩子结点
private BinaryTreeNode right;//指向左孩子结点
public BinaryTreeNode(int data) {
this.data = data;
this.left = null;
this.right =null;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public BinaryTreeNode getLeft() {
return left;
}
public void setLeft(BinaryTreeNode left) {
this.left = left;
}
public BinaryTreeNode getRight() {
return right;
}
public void setRight(BinaryTreeNode right) {
this.right = right;
}
}
3.2 二叉树的递归遍历实现
package Binary_Tree_Study;
import java.util.Stack;
import java.util.Queue;
import java.util.LinkedList;
/**
* Created by Administrator on 2018/5/19.
*/
public class BinaryTree {
private BinaryTreeNode root;//二叉树根结点
public BinaryTree() {
this.root = null;
}
/* 建立二叉树:
1
/ \
2 3
/ \ /
4 5 6
*/
public BinaryTreeNode createBinaryTree() {
root = new BinaryTreeNode(1);
root.setLeft(new BinaryTreeNode(2));
root.setRight(new BinaryTreeNode(3));
root.getLeft().setLeft(new BinaryTreeNode(4));
root.getLeft().setRight(new BinaryTreeNode(5));
root.getRight().setLeft(new BinaryTreeNode(6));
return root;
}
//先序遍历:非递归方法
public void PreOrderIterative(BinaryTreeNode root) {
BinaryTreeNode temp = root;
Stack s = new Stack();
while (temp != null || !s.isEmpty()) {
while (temp != null) { //遇到一个结点,就把它压栈并访问它,然后去遍历它的左子树;
s.push(temp);
System.out.print(temp.getData() + " ");
temp = temp.getLeft();
}
if(!s.isEmpty()) {
temp = s.pop();//当左子树遍历结束后,从栈顶弹出这个结点;
temp = temp.getRight();//然后按其右指针再去先序遍历该结点的右子树
}
}
}
//中序遍历:非递归方法
public void InOrderIterative(BinaryTreeNode root) {
BinaryTreeNode temp = root;
Stack s = new Stack();
while (temp != null || !s.isEmpty()) {
while (temp != null) { //遇到一个结点,就把它压栈,并去遍历它的左子树;
s.push(temp);
temp = temp.getLeft();
}
if(!s.isEmpty()) {
temp = s.pop();//当左子树遍历结束后,从栈顶弹出这个结点并访问它;
System.out.print(temp.getData() + " ");
temp = temp.getRight();// 然后按其右指针再去中序遍历该结点的右子树
}
}
}
//后序遍历:非递归方法
public void PostOrderIterative(BinaryTreeNode root) {
BinaryTreeNode temp = root;
BinaryTreeNode pre = null;//标记访问序列中前一个二叉树节点(当前节点的之前访问的节点)
Stack s = new Stack();
while (temp != null || !s.isEmpty()) {
while (temp != null) {
s.push(temp);
temp = temp.getLeft();
}
if(!s.isEmpty()) {
temp = s.peek();
//如果一个节点右孩子是空,或者右孩子刚被访问过,那么就访问该节点。否则就往右孩子走。
if(temp.getRight() == null || temp.getRight() == pre) {
System.out.print(temp.getData() + " ");
s.pop();
pre = temp;
temp = null;
}else {
temp = temp.getRight();
}
}
}
}
//层序遍历
public void LevelOrder(BinaryTreeNode root) {
BinaryTreeNode temp;
Queue q = new LinkedList();
if(root == null)
return;
q.add(root);
while (!q.isEmpty()) {
temp = q.poll();//移除并返问队列头部的元素
System.out.print(temp.getData() + " ");
if (temp.getLeft() != null) {
q.add(temp.getLeft());//左孩子入队
}
if (temp.getRight() != null) {
q.add(temp.getRight());//右孩子入队
}
}
}
}
package Binary_Tree_Study;
/**
* Created by Administrator on 2018/5/19.
*/
public class BinaryTreeTest {
public static void main(String[] args) {
BinaryTree tree = new BinaryTree();
BinaryTreeNode root = tree.createBinaryTree();
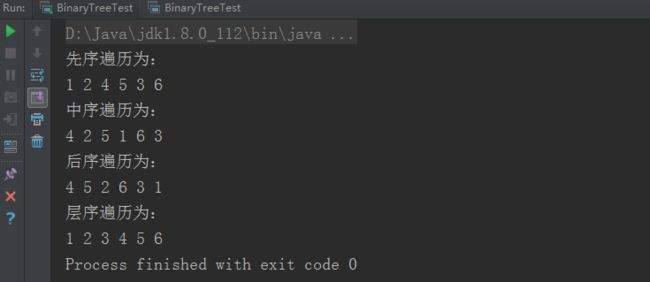
System.out.println("先序遍历为:");
tree.PreOrderIterative(root);
System.out.println("\n中序遍历为:");
tree.InOrderIterative(root);
System.out.println("\n后序遍历为:");
tree.PostOrderIterative(root);
System.out.println("\n层序遍历为:");
tree.LevelOrder(root);
}
}
4 参考资料
[1] 二叉树的非递归遍历
[2] 浙大数据结构慕课--中序非递归遍历
[3] 后序遍历---百度百科
[4] Level Order Tree Traversal
[5] 梦回考研——复习二叉树的各种遍历
[6] 数据结构与算法(一):二叉树的非递归遍历