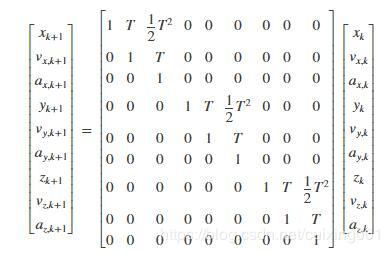基于卡尔曼滤波算法在三维球轨迹中跟踪应用
关于卡尔曼滤波跟踪算法的理解文章实在太多,绝大多数都在叙述算法原理和一些理解,而且一般举例都限于一维直线运动或者二维平面运动,故在此不做过多的重复表述,有关原理理解性的文章请参考本博客后的reference。而此篇博客旨在从另外角度去逐步实现卡尔曼滤波在三维轨迹球预测上来,假设读者能够理解卡尔曼的5个公式(2个predict,3个update/correction),不懂可以参考文后的reference,通过三种方法(两种通过调用API函数实现,另一种根据原理公式)去加以实现,从而做到对算法的深刻理解和运用。
一、问题描述
平时我们所说的卡尔曼滤波算法指的是离散线性滤波算法,其前提条件是假设物体的运动规律满足匀速直线运动(速度恒定)或者匀加速/减速(加速度恒定)运动,从三维空间运动来看:
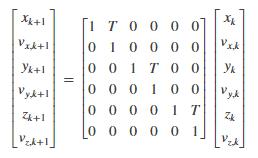
速度恒定时
- 球的运动规律表示为:
- 通过测量矩阵得到球的三维位置可以表示为:
加速度恒定时
- 球的运动规律表示为:
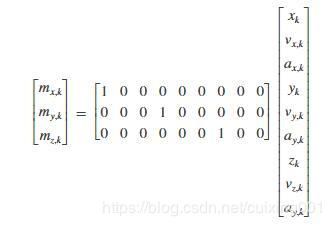
- 通过测量矩阵得到球的三维位置可以表示为:
现给出具体问题的描述,三维空间中一个做加速度恒定运动的球,假设理论轨迹为抛物面中的一条斜截线,其运动轨迹方程具体表达式为:
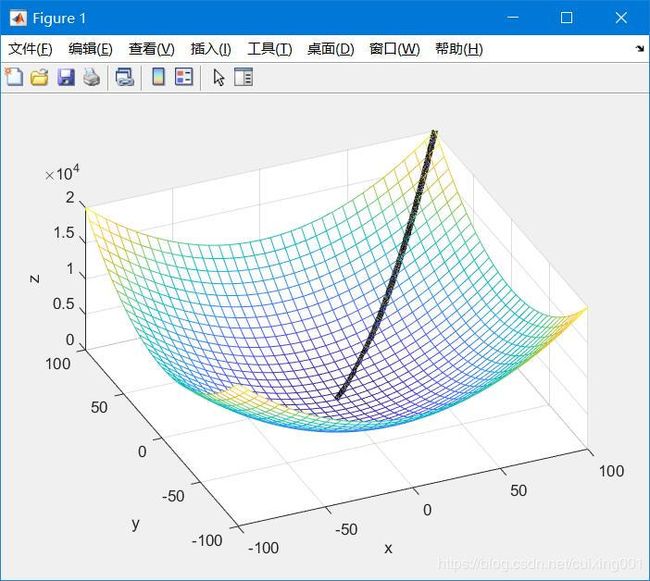
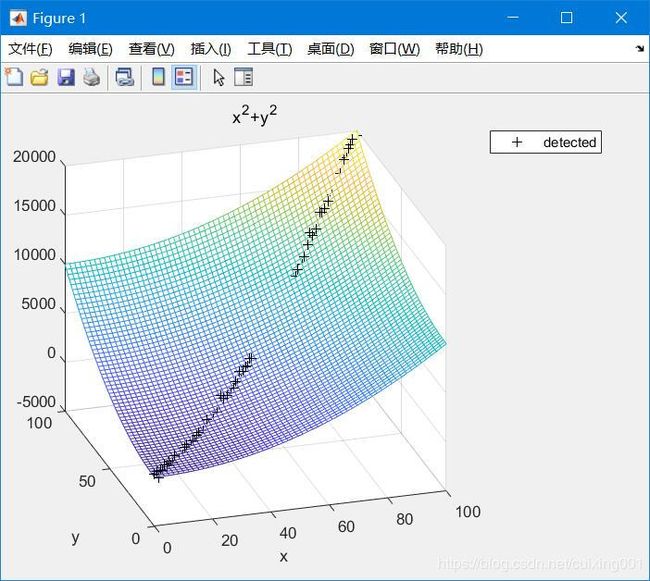
球从原点(0,0,0)出发,向上做抛物运动,图像上显示为黑色的一条线,如下图所示:
由于现实中球的实际运动轨迹并非像上面十分完美,因为还要考虑空气阻力影响,而且还存在某个时间段球被遮挡的情况,一般球的运动的噪声符合高斯分布。因此后面可以生成一系列带噪声的模拟三维球坐标数据,然后删除中间某段数据当作被遮挡的情况。
二、具体实现
生成原始检测/测量数据,“+”表示带噪声分布的数据,中间一段没有的数据表示被遮挡丢失,程序如下:
% 带高斯噪声的三维坐标数据
close all;
x = 0:100;
y = x;
z = x.^2+y.^2+500*randn(1,101);
empty_start_index = 50;
empty_end_index = 70;
delete_index = empty_start_index:empty_end_index;
x(delete_index) = [];
y(delete_index) = [];
z(delete_index) = [];
plot3(x,y,z,'k+')
grid on;
hold on;
ezmesh(@(x,y)x.^2+y.^2,[0,100])
legend('detected')跟踪算法的逻辑为:有detect的点,就同时需prediction和correction;没有detect的点就只能prediction。
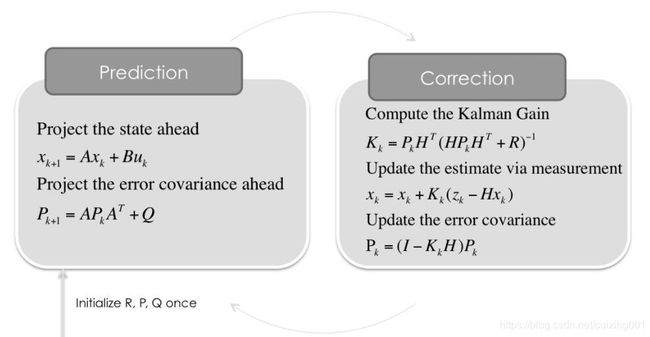
- method 1: 根据卡尔曼的5个公式迭代更新球的位置,这里直接给出五个公式:
结合球的三维运动规律和上面5个公式,对其中的符号做出个人理解说明或定性分析:
式中,A为状态转移矩阵,描述物体运动满足的规律,本问题为9*9矩阵;
B为控制矩阵,描述控制量uk对物体运动的附加控制,本问题为空;
P为状态误差估计协方差矩阵,它能描述模型误差在每代中的传递情况,每次迭代会更新此矩阵,第一次初始如果给比较大的值算法在前几次迭代中会更快适应检测值,但是更小可能忽略噪声,本问题为9*9矩阵;
Q为处理噪声矩阵,它描述预测模型带来的不确定情况,值越大越表明预测越不可靠,算法最后结果更靠近测量值,本问题为9*9矩阵,每次不更新此值;
R为测量噪声矩阵,它描述测量/检测过程中带来的不确定情况,值越大越表明测量越不可靠,算法最后结果更靠近预测值,本问题为3*3矩阵(因为有三个测量量,分别为x,y,z),每次不更新此值;
H为测量矩阵,它描述通过某种手段测量的状态值的矩阵,本问题为3*9矩阵;
K为增益系数,它能够融合测量和预测的状态量, 根据系数大小权衡测量和预测的结果,而且它也可把测量量zk的维数转换到xk的维数,本问题zk维数为3*1,xk维数为9*1,K为9*3.
记上图中prediction 2个公式为(1),(2),correction/update 3个公式为(3),(4),(5),对应程序注释中eqution,其实现为:
%% 3D坐标系下常加速度模型
deltaT = 1;
A = [1,deltaT,0.5*deltaT^2, 0,0,0, 0,0,0;
0,1,deltaT, 0,0,0, 0,0,0;
0,0,1, 0,0,0, 0,0,0;
0,0,0, 1,deltaT,0.5*deltaT^2, 0,0,0;
0,0,0, 0,1,deltaT, 0,0,0;
0,0,0, 0,0,1, 0,0,0;
0,0,0, 0,0,0, 1,deltaT,0.5*deltaT^2;
0,0,0, 0,0,0, 0,1,deltaT;
0,0,0, 0,0,0, 0,0,1];
B = [];
H = [1,0,0, 0,0,0, 0,0,0;
0,0,0, 1,0,0, 0,0,0;
0,0,0, 0,0,0, 1,0,0];
p = diag([5e+7,3e+7,1e+5]);% 小p为3*3对角矩阵,初始值,后续会迭代更新此值
P = blkdiag(p,p,p);% 大P扩展为9*9对角矩阵
Q = diag(ones(1,9));% 处理噪声矩阵,正数的对称矩阵
R = 2.5*10^7*diag([1,1,1]);% 测量噪声矩阵,3*3大小
%% 第一种方法,根据卡尔曼5个公式撰写,实现predict, correct方法
initState = [x(1),0,0, y(1),0,0, z(1),0,0]; % [x;vx;ax;y;vy;ay;z;vz;az]
previousLocate = initState';
for i = 1:101
predictLocate = A*previousLocate;% equation 1
P = A*P*A'+Q; % equation 2
previousLocate = predictLocate;
if iempty_end_index)
detectLocate = [x(empty_start_index),y(empty_start_index),z(empty_start_index)]';
% update
K = P*H'/(H*P*H'+R); % equation 3
predictLocate = previousLocate+K*(detectLocate-H*previousLocate);% equation 4
P = (eye(9)-K*H)*P;% equation 5
empty_start_index = empty_start_index+1;
end
previousLocate = predictLocate;
pause(0.1);
plot3(predictLocate(1),predictLocate(4),predictLocate(7),'ro');
fprintf('%d\n',i);
end
xlabel('x');ylabel('y');zlabel('z')
fmesh(@(x,y)x.^2+y.^2,[0,100]);
legend('detection','prediction') - method2,根据A,B,H,Q,R等给出的矩阵,采用vision.KalmanFilter配置卡尔曼滤波算法class,为对比说明,这里依旧采用方法一的这些矩阵,程序如下:
%% 3D坐标系下常加速度模型
deltaT = 1;
A = [1,deltaT,0.5*deltaT^2, 0,0,0, 0,0,0;
0,1,deltaT, 0,0,0, 0,0,0;
0,0,1, 0,0,0, 0,0,0;
0,0,0, 1,deltaT,0.5*deltaT^2, 0,0,0;
0,0,0, 0,1,deltaT, 0,0,0;
0,0,0, 0,0,1, 0,0,0;
0,0,0, 0,0,0, 1,deltaT,0.5*deltaT^2;
0,0,0, 0,0,0, 0,1,deltaT;
0,0,0, 0,0,0, 0,0,1];
B = [];
H = [1,0,0, 0,0,0, 0,0,0;
0,0,0, 1,0,0, 0,0,0;
0,0,0, 0,0,0, 1,0,0];
p = diag([5e+7,3e+7,1e+5]);% 小p为3*3对角矩阵,初始值,后续会迭代更新此值
P = blkdiag(p,p,p);% 大P扩展为9*9对角矩阵
Q = diag(ones(1,9));% 处理噪声矩阵,正数的对称矩阵
R = 2.5*10^7*diag([1,1,1]);% 测量噪声矩阵,3*3大小
% 第二种方法配置,上面参数与方法一相同
kalmanFilter = vision.KalmanFilter(A,H,B);
kalmanFilter.State = [x(1),0,0, y(1),0,0, z(1),0,0]; % [x;vx;ax;y;vy;ay;z;vz;az]
kalmanFilter.StateCovariance = P;
kalmanFilter.ProcessNoise = Q;
kalmanFilter.MeasurementNoise = R;
% 循环迭代更新
for i = 1:101
predictLocate = predict(kalmanFilter);
if iempty_end_index
detectLocate = [x(empty_start_index),y(empty_start_index),z(empty_start_index)];
predictLocate = correct(kalmanFilter,detectLocate);
empty_start_index = empty_start_index+1;
end
pause(0.1);
plot3(predictLocate(1),predictLocate(2),predictLocate(3),'ro');
fprintf('%d\n',i);
end
xlabel('x');ylabel('y');zlabel('z')
fmesh(@(x,y)x.^2+y.^2,[0,100]);% 或者ezmesh代替函数fmesh
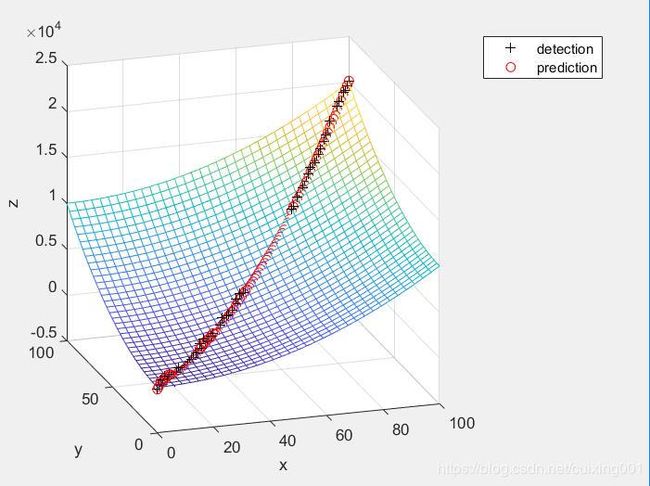
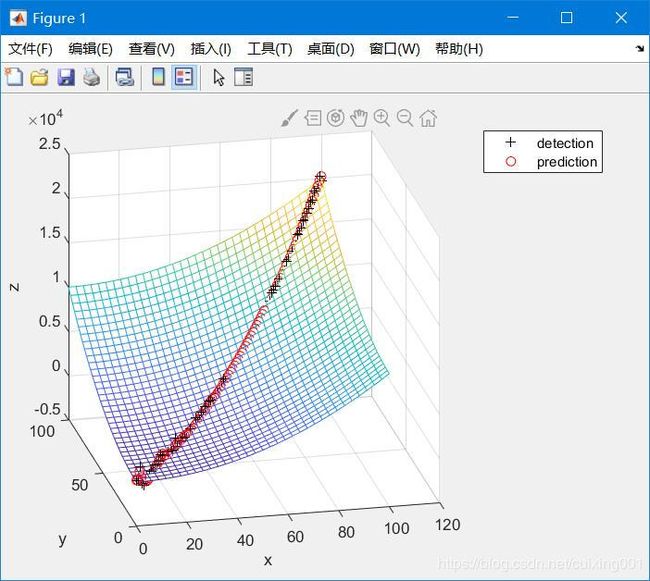
legend('detection','prediction') - method 3,这种方法最简介了,采用configureKalmanFilter函数直接配置其对象,省去上面A,K,B,H,Q,R等指定繁琐过程,里面内部实现原理是一样的,只需简单进行配置即可使用。(该函数中参数
InitialEstimateError对应P矩阵,MotionNoise对应Q矩阵,MeasurementNoise对应R矩阵,只是形式上扩展了维度而已),实现和效果图如下:
% 第三种方法,很简单的配置,参数一致
initialLocation = [x(1),y(1),z(1)]; % [x;y;z]
kalmanFilter = configureKalmanFilter('ConstantAcceleration',...
initialLocation, [500 300 1]*1e5, [1 1 1], 2.5*10^7);
% 循环迭代更新
for i = 1:101
predictLocate = predict(kalmanFilter);
if iempty_end_index
detectLocate = [x(empty_start_index),y(empty_start_index),z(empty_start_index)];
predictLocate = correct(kalmanFilter,detectLocate);
empty_start_index = empty_start_index+1;
end
pause(0.1);
plot3(predictLocate(1),predictLocate(2),predictLocate(3),'ro');
fprintf('%d\n',i);
end
xlabel('x');ylabel('y');zlabel('z')
fmesh(@(x,y)x.^2+y.^2,[0,100]);% 或者ezmesh代替函数fmesh
legend('detection','prediction') 本博客完整代码下载:https://download.csdn.net/download/cuixing001/10792450
Reference:
https://blog.csdn.net/AdamShan/article/details/78248421
https://www.zhihu.com/question/23971601
https://blog.csdn.net/u012554092/article/details/78290223
http://mini.eastday.com/bdmip/180326002020911.html#
https://www.cnblogs.com/YangQiaoblog/p/5462453.html
https://loopvoid.github.io/2017/03/26/Opencv%E5%AE%9E%E7%8E%B0Kalman%E6%BB%A4%E6%B3%A2%E5%99%A8/
https://ww2.mathworks.cn/help/driving/ug/linear-kalman-filters.html