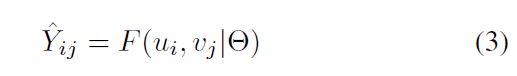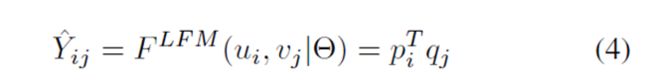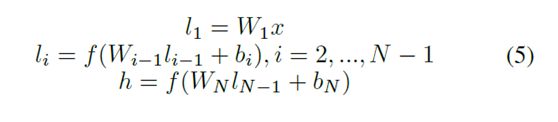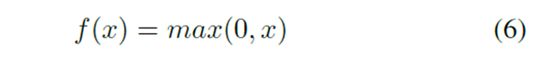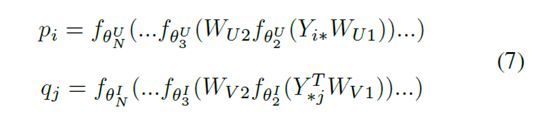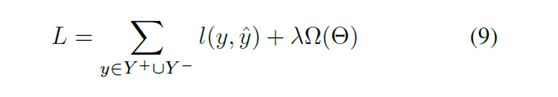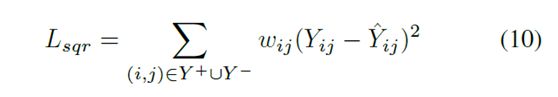Author:Hong-Jian Xue, Xin-Yu Dai, Jianbing Zhang, Shujian Huang, Jiajun Chen
引言
推荐系统通常使用用户-项交互评分、隐式反馈和辅助信息进行个性化推荐。矩阵分解是根据用户和项目之间的相似性来预测单个用户的一组项目的个性化排序的基本思想。本文提出了一种新的基于神经网络结构的矩阵分解模型。首先,我们构建了一个具有显式评分和非偏好隐式反馈的用户项矩阵。以该矩阵为输入,提出了一种深层次结构学习体系结构,为用户和项目的表示提供了一个公共的低维空间。其次,我们设计了一种新的基于二元交叉熵的损失函数,在这里,为了更好地进行优化,我们考虑了显式的评分和隐式的反馈。实验结果显示了我们提出的模型和损失函数的有效性。在几个基准数据集上,我们的模型胜过了其他最先进的方法。我们还进行了大量实验来评估不同实验环境下的表现。
介绍
在信息爆炸的时代,信息超载是我们面临的困境之一。推荐系统(RSs)有助于解决这个问题,因为它们帮助确定向个人消费者提供哪些信息,并允许在线用户快速找到符合他们需求的个性化信息。如今,RSs在电子商务平台中无处不在,比如亚马逊的图书推荐、Last.com的音乐、Netflix的电影以及CiteULike的推荐。
协同过滤(CF)推荐方法在研究界得到了广泛的研究并广泛应用于工业领域。 他们基于简单的直觉,即如果用户在过去对项目类似地评价,他们很可能在未来对其他项目进行类似评价。作为各种协同过滤技术中最流行的一种方法,矩阵分解(MF) 学习用于表示用户或项目的潜在空间,并由于其可扩展性、隐含性和灵活性成为推荐的标准模型。在潜在空间中,推荐系统根据用户和项目之间的相似性预测每个用户的一组项目的个性化排序。
用户-项目交互矩阵中的评分是一种显性知识,在早期的推荐方法中得到了深入的应用。由于用户对项目的评分值存在差异,因此使用偏向矩阵分解来提高评分预测。为了克服评分的稀疏性,将额外的数据集成到MF中,如社会关系的社会矩阵分解、项目内容或评论文本的主题矩阵分解等。
然而,仅建模观察到的评分不足以形成良好的TOP-N推荐。 在推荐系统中应用了隐性反馈,如购买历史和未观测评分等。SVD++模型首先对评分矩阵进行隐式反馈分解,然后是许多推荐系统的技术。
近年来,由于具有强大的代表性学习能力,深度学习方法已成功应用在计算机视觉、语音识别、自然语言处理等领域. 在推荐系统中也做了一些努力来应用深度学习模型。首先提出了限制玻尔兹曼机模型,对用户在项目上的显式评分进行建模。自动编码器和去噪自动编码器也被应用于推荐。这些方法的关键思想是通过学习具有明确历史评分的隐藏结构来重建用户的评分。 隐性反馈也被应用于这一深度学习研究的推荐领域。 一项扩展工作提出了一种协同去噪自动编码器(CDAE),用隐式反馈对用户的偏好进行建模。另一项神经协同过滤(NCF)工作被提出来用多层前馈神经网络对用户 - 项目交互进行建模。 以上两个最近的作品仅利用项目建议的隐式反馈而不是明确的评价反馈。
在本文中,为了同时利用显式评分和隐式反馈,我们提出了一种新的神经矩阵分解模型,用于Top-N推荐。我们首先构造一个既有显式评分又有非偏好隐式反馈的用户 - 项目矩阵,这与其他只使用显式评分或仅使用隐式评分相关方法不同。通过这个完整的矩阵(显式评分和为零的隐式反馈)作为输入,提出了一种神经网络架构来学习一个共同的潜在低维空间来表示用户和项目。 该体系结构受深层结构化语义模型的启发,该模型已被证明可用于网络搜索[Huang et al。,2013],它可以通过多层非线性投影将查询和文档映射到潜在空间。 另外,我们设计了一个基于交叉熵的新损失函数,其中包括显式评分和隐式反馈的考虑。
总而言之,我们的主要贡献如下。
- 我们提出了一种新的深层矩阵分解模型,用神经网络将用户和项目映射到具有非线性投影的公共低维空间中。我们使用一个矩阵,包括显式评分和非偏好隐式反馈作为我们的模型的输入。
- 我们设计了一个新的损失函数同时考虑显式评分和隐式反馈以实现更好的优化。
- 实验结果表明,在TOP-N推荐中,本文提出的模型的有效性优于其他先进的方法。
本文的组织结构如下。第2节介绍了问题陈述。在第3节中,我们介绍了模型的体系结构和细节。在Section4中,我们给出了几个基准数据集的实证结果。最后一节将讨论一些未来的工作。
2 问题阐述
现有的大多数推荐解决方案都采用方程1来构造Y。他们认为所有观察到的评级都与1相同。本文用方程2构造了Y矩阵。用户Ui对项目的评分Rij仍然保留在Y。我们认为,公式2中的显式评分对于推荐来说是不平凡的,因为它们表明了用户对某项的偏好程度。同时,我们在评分未知的情况下标记为零,这被称为非偏好隐式反馈。
推荐系统通常被定义为估计矩阵Y中每个未观察到的条目的评分,用于对项目进行排序。基于模型的方法假定有一个底层模型可以生成所有的评分如下。
其中
表示用户ui与项目vj之间的交互Yij的预测值,θ表示模型参数,F表示将模型参数映射到预测分数的函数。基于此功能,我们可以实现向单个用户推荐一组项目的目标,以最大化用户的满意度。
现在,下一个问题是如何定义这样的函数F.隐语义模型(LFM)简单地应用pi,qj的点积来预测,如下所示:pi和qj分别表示ui和vj的潜在表示。
最近,神经协同过滤(NCF)提出了一种利用多层感知器自动学习f函数的方法,该方法的动机是学习用户与项目之间的非线性交互。
在本文中,我们遵循用内积来计算用户和项目之间相互作用的潜在因素模型。我们不遵循神经协同过滤,因为我们试图通过深度表示学习体系结构来获得用户和项目之间的非线性连接。
我们给出下节中使用的符号。u表示用户和V表示项。i和j分别索引u和v。Y代表由公式2确定的用户-项交互矩阵,Y+代表显示评分,Y-代表所有零元素,Y-sample代表负采样,Y+ ∪Y-sample代表训练矩阵,我们用Yi代表第i行所有元素,Yj代表第j列所有元素,第i行第j列用Yij表示。
3 本文提出模型
在本部分中,我们首先简要介绍了深层结构语义模型,这启发了我们提出的方法。然后,我们展示了我们提出的架构,以在一个潜在的低维空间中表示用户和项目。最后,我们给出了优化后的损失函数,然后是模型训练算法。
3.1 深度结构化予以模型
深度结构化语义模型(DSSM)被提出用于网络搜索。 它使用深度神经网络对给定查询的一组文档进行排名。 DSSM首先将查询和文档映射到具有非线性多层投影的公共较低语义空间。然后对于web搜索排名,查询与每个文档的相关性是通过查询和文档的低维向量之间的余弦相似度来计算的。对深度神经网络进行了区别训练,以最大限度地提高查询和匹配文档的条件概率。
DSSM已应用于用户建模。与我们的工作不同的是,它专注于为用户建模,并拥有丰富的额外功能,比如网页浏览历史和搜索查询。我们只使用观察到的评分和观察反馈,因为我们关注的是传统的top-N推荐问题。
3.2 深度矩阵分解模型
如第2节所述,我们根据方程2形成矩阵y。以矩阵y为输入,提出了一种将用户和项目投影到潜在结构化空间的深层神经网络结构。图1说明了我们所提出的体系结构。
figure 1: The architecture of Deep Matrix Factorization Models
从矩阵Y中,将每个用户ui表示为Yi的高维矢量,其表示第i个用户对所有项目的评分。 每个项目vj被表示为Yj的高维矢量,其表示所有用户中的第j项目的评级。 在每一层中,每个输入矢量都映射到另一个新空间中的矢量。 在形式上,如果我们用x表示输入矢量,用y表示输出矢量,用li表示中间隐藏层; i = 1,…,N-1,Wi的第i个权重矩阵,bi的第i个偏倚项以及h为最终输出潜在表示。 我们有
我们使用ReLU作为输出层和隐藏层li的激活函数; i= 2,…,N-1:
在我们的体系结构中,我们有两个多层网络分别对u和v的表示进行转换。通过神经网络,用户ui和项vj最终映射到潜在空间中的低维矢量,如公式7 然后根据公式8测量用户ui和项目vj之间的相似度。
这里WU1和WV1分别是U和V的第一层权重矩阵,以及第二层的WU2和WV2,等等。
在我们的体系结构中,除了多层表示学习外,我们还要再次强调,就我们所知,这是第一次直接使用交互矩阵作为表示学习的输入。正如我们前面提到的,Yi代表用户对所有项目的评分。它可以在某种程度上表明用户的全局偏好。Yj代表了一个项目上所有用户评价。它可以在某种程度上表明一个项目的概要(轮廓profile)。我们认为,用户和项目的这些表示对于最终的低维表示非常有用。
3.3 损失函数
推荐模型的另一个重要组成部分是根据观察到的数据和未观察到的反馈,为模型优化定义一个合适的目标函数。一般的目标函数如下。
l(.) 代表损失函数, Ω (.) 是正则化。
对于推荐系统来说,两种类型的目标函数是常用的,分别是点的和成对的。简单地说,我们在本文中使用了点的目标函数,并将成对的版本留给我们未来的工作。
损失函数是目标函数中最重要的部分。在许多现有的模型中,平方损失在很大程度上是被执行的。
平方损失的使用是基于一个假设,即观测是由高斯分布产生的。但是,对于隐式反馈,平方损失不能很好地使用,因为对于隐式的数据,目标值Yij是一个二进制的1或0,表示i是否与j进行了交互。在接下来的内容中,[He et al., 2017]提出了一种对隐式数据的二元属性特别关注的损失函数,如下所示。
这种损失实际上是二元交叉熵损失(简称ce),将隐含反馈的推荐作为二进制分类问题处理。
综上所述,平方损失关注显式评分,而交叉熵损失则关注隐式评分。在本文中,我们设计了一个新的损失函数,将显式的评分合并到交叉熵损失中,这样就可以将显式和隐式信息结合在一起进行优化。我们将我们的新损失命名为归一化交叉熵损失(简称nce),它在公式12中给出。
我们使用max(R)(5星系统中为5)进行归一化,这是所有评分的最大值,因此不同的Yij值对损失有不同的影响。
3.4 训练算法
对于交叉熵损失,由于Yij的预测分数可以是负数,我们需要使用公式13来改变原始的预测。让M是一个非常小的数,我们在实验上设置为1.0e-6.
我们在算法1中描述了详细的训练方法。
在算法1中,我们给出了DMF模型的高级训练过程。对每一层的权重矩阵WU和WV的参数进行训练,利用反向传播对模型参数进行批量更新。我们的算法复杂度与矩阵的大小和网络的层次是线性的。
4 实验
在本节中,我们将进行实验,以证明我们所提出的架构和改进的损失函数的有效性。我们还做了一些广泛的实验来比较不同实验设置的性能,比如负采样率,网络层数等等。
4.1 Experimental Settings
数据集
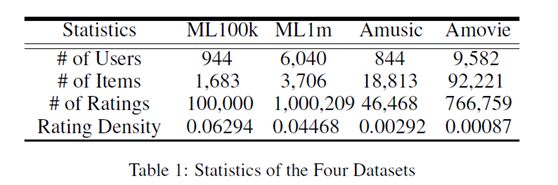
我们用在推荐系统中广泛使用的四个数据集评估我们的模型:MovieLens 100K(ML100k),MovieLens 10M(ML1m), Amazon music(Amusic), Amazon movies(Amovie)。他们在网站上可以公开访问。对于MovieLens数据集,我们不处理它,因为它已经被过滤了,而对于Amazon dataset,我们过滤了数据集,所以类似于MovieLens数据,只有那些至少有20个交互的用户和至少有5个交互的条目被保留[Wu et al., 2016;他et al .,2017)。表1给出了四个数据集的统计数据。
评估建议
为了评估项目推荐的绩效,我们采用了leave-one-out评估,在文献[He et al., 2016;Kingma和英航,2014;他et al .,2017)中得到了广泛的应用。我们将最新的交互作为每个用户的测试项目,并利用剩余的数据集进行训练。由于在评估过程中对每个用户进行排序太费时间了,根据[Koren, 2008;He et al., 2017]中,我们随机抽取了100个没有被用户交互的项目。在100个项目和测试项目中,我们根据预测得到排名。我们还使用命中率(HR)和标准化折扣累积增益(NDCG)来评估排名性能。在我们的实验中,我们将这两个指标的排名列表截断为10。因此,HR直觉地衡量测试项目是否在前10名列表中,而NDCG衡量的是排名质量,它将得分更高的分数分配给顶级排名。
详细实施
我们基于Tensorflow3实施了我们提出的方法,该方法将在接受后公开发布。 为了确定DMF方法的超参数,我们为每个用户随机抽取一个交互作为验证数据并调整超参数。 在训练我们的模型时,我们对每个正实例采样了7个负实例。对于神经网络,我们用高斯分布随机初始化模型参数(均值为0,标准差为0.01),用小批量Adam [Kingma and Ba, 2014]对模型进行优化。我们将批处理大小设置为256,将学习速率设置为0.0001。
4.2 性能比较
在本小节中,我们将使用以下方法对所建议的DMF进行比较。由于我们的方法旨在建模用户与项目之间的关系,我们主要与用户项目模型进行比较。我们忽略了与SLIM [Ning and Karypis,2011],CDAE [Wu et al。,2016]等项目模型的比较,因为性能差异可能是由于用户模型的个性化造成的。我们也省去了与MV-DSSM [Elkahky et al., 2015]的比较,因为它使用了大量辅助的额外数据,并对自己的数据集进行评估。
ItemPop
它根据互动次数判断它们的受欢迎程度来排列项目。 这是一种非个性化方法,其性能通常用作个性化方法的基准.
ItemKNN这是一种基于标准的基于项目的协同过滤方法,用于亚马逊商业(Sarwar et al., 2001;林登et al .,2003)。
eALS这是用于推荐的使用平方损失的最先进的MF方法。它使用所有未被观察到的交互作为负面实例,并以非一致的方式对其进行加权。我们以[他等人,2016]的方式对其超参数进行了调整。
这是一种最先进的MF方法,用于使用交叉熵损失的项目推荐。这是我们最相关的工作。与我们的模型不同,它只使用隐式反馈,并对用户和项目的表示进行随机初始化。在此之后,它利用多层感知器来学习用户项交互功能。我们将神经矩阵分解命名为“纽曼式”,在他们的提案模型中表现出最佳的性能。我们以[他等人,2017]的方式对其超参数进行了调整。
DMF-2-ce这是我们提出的深度矩阵分解模型,网络中有2层,交叉熵作为损失函数。 我们使用矩阵,包括显式评级和隐式反馈作为DMF的输入。我们将该模型命名为DMF-2-ce。
DMF-2-nce DMF-2-nce具有与DMF-2-ce中相同的2层深度,除了它使用归一化的交叉熵损失。
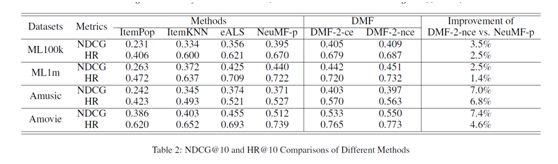
表2总结了比较结果。它证明了我们提出的架构和损失函数的有效性。 就所提出的架构而言,在几乎所有数据集中,与其他方法相比,我们的两个模型在NDCG和HR两个方面均达到最佳性能。 即使与最先进的NeuMF-p方法相比,DMF-2nce分别在NDCG和HR度量方面获得2.5-7.4%(平均5.1%)和1.4-6.8%(平均3.8%)的相对改进。 至于损失函数,我们比较了两个模型的性能。 DMF-2-nce的效果比DMF-2-ce好,除了Amusic的数据集。
4.3 输入矩阵对DMF的影响
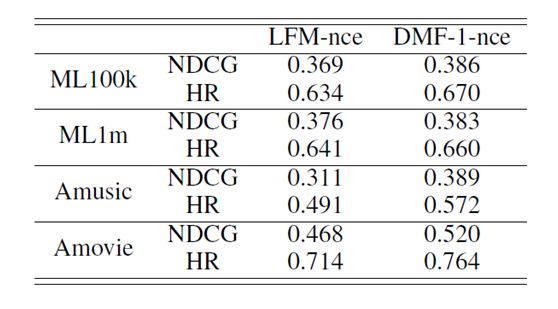
表3:不同输入矩阵的结果。LFM-nce随机初始化输入矩阵。DMF-1-nce使用Y矩阵作为输入。它们都执行1层投影。
在DMF中,我们使用交互矩阵Y作为输入。如果我们随机初始化每个用户和每一个项作的表示向量为一层DMF模型的输入,那么模型将是一个标准的潜在因子分解模型(LFM)。为了测试Y的输入矩阵的有效性,我们对LFM-nce和DMF-1-nce的两种模型进行了实验。它们在网络中都有一个层,并且使用相同的损失函数。从表3可以看出,在输入矩阵中,DMF-1-nce在LFM-nce上取得了显著的改善。
4.4 对超参数的敏感度
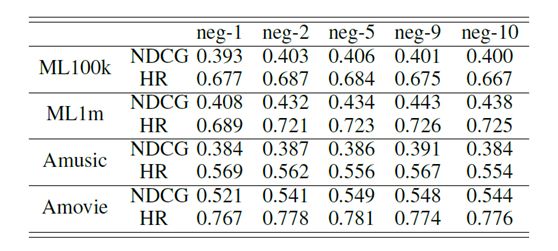
表4:不同负采样率模型的结果。
负采样率
在3.4节所示的算法1中,我们需要从未观测到的数据中抽取负面实例进行训练。 在这个实验中,我们应用不同的负采样率来观察性能方差(例如neg-5意味着我们将负采样率设置为5)。 从表4的结果中,我们可以发现更多负面事例似乎对提高绩效有用。 对于这四个数据集,最佳的负采样率大约为5,这与以前的工作结果一致[He et al。,2017]。
网络层的深度
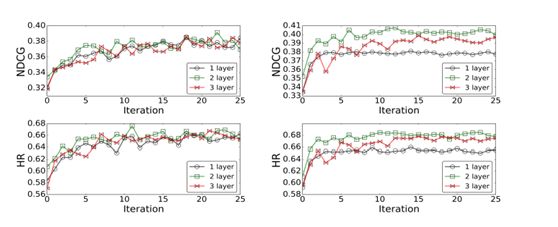
在我们提出的模型中,我们通过具有多个隐藏层的神经网络将用户和项目映射到低维表示。 我们对Ml数据集进行了广泛的实验,以调查具有不同数量隐藏层的模型。 有关详细比较,图2显示了不同层次的每次迭代的性能。 对于空间限制,我们只是在ML数据集上呈现结果。 如图2所示,在大型ML1m数据集上,我们的2层模型说明了最佳性能。 在相对较小的ML100k数据集上,2层几乎可以获得最佳性能,但不是稳定且显着。 更深的层看起来没有用,而3层模型甚至会降低性能。
图2:不同深层模型的结果。左:ML100k;右:ML1m。
最终潜在空间的因素
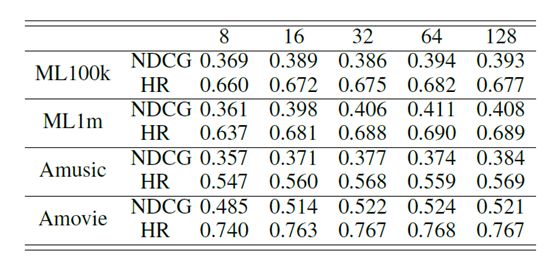
除了隐藏层的数量之外,每层中的因素可能是我们模型中的另一个敏感参数。为了简单起见,我们只是比较顶部最终潜在空间上不同数量因素的性能。 我们将实验进行到两层模型,并将顶层上的因子数量从8个设置为128个。如表5所示,除了Amusic数据集以外,具有64个因子的最终层获得最佳性能。 在Amusic数据集上,最佳性能显示128个因子。 当数据集非常稀少时,包含更多因子的最终表示可能更有用。
表5:最终潜在空间不同因素模型的结果。
5 结论与未来的工作
本文提出了一种基于神经网络结构的矩阵分解模型。通过神经网络体系结构,将用户和项目投射到潜在空间中的低维向量中。在我们提出的模型中,我们充分利用了显性评分和隐性反馈两种方式。我们所提出的模型的输入矩阵包括显式评分和非偏好反馈。另一方面,我们也设计了一个新的损失函数来训练我们的模型,在这个模型中,我们考虑了显式和隐式反馈。几个基准数据集的实验证明了我们所提出的模型的有效性。
在未来,我们有两个方向来扩展我们的工作。成对的目标函数是推荐系统的另一种可选方式。我们将用成对的目标函数来验证我们的模型。由于稀疏和大量缺失的未观测数据,许多作品试图将辅助的额外数据整合到推荐系统中,如社会关系、评论文本、浏览历史等。这给了我们另一个有趣的方向来扩展我们的模型和额外的数据。