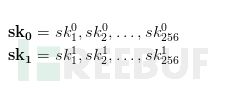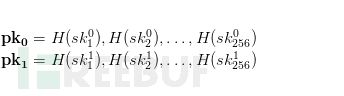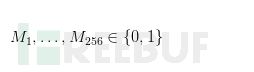Hash签名算法入门

在这篇文章中主要讲述了签名算法的发展历程，分析了基于哈希函数的签名算法的原理及优缺点。

在过去的几年间，我有幸观察到两种矛盾又有吸引力的趋势。第一种是我们终于开始使用研究员花40年设计的密码学。从加密信息到手机安全再到数字加密货币，我们每天都可以从例子中看到这一点。

第二种趋势是密码学正在为所有美好时光的结束做准备。

在我完成这些之前，我要强调的是，这不是一篇关于量子计算灾难的文章，也不是一篇关于密码学在21世纪取得的成就的文章。而是要讨论一些不确定的东西。本文将介绍有史以来最简单的加密技术之一：hash签名算法。

hash签名方案是在20世纪70年代后期由LeslieLamport首次发明的，由Ralph Merkle等人进行改良。在很长一段时间里，它们都被认为是密码学中不会被触碰的地方，主要是因为它们生成相应的大签名（在其他难题中）。然而在近几年，这些结构有了某种复兴的景象，不像基于RSA的签名或离散对数假设，这种复兴很大程度上是因为他们在很大程度上被视为对像Shor算法这样严重的量子攻击的抵抗。

先来讲一下背景

背景：Hash函数和签名方案

为了理解hash签名，先了解加密散列函数是很重要的。这些函数获取一些输入串（通常是任意长度的）然后把生成的具有固定长度的“摘要”作为输出。常见的加密散列函数，比如SHA2，SHA3或者Blake2生成的摘要长度在256bit到512bit之间，

为了让函数H(.)成为 “加密”hash，它必须达到某种特殊的安全需求。这些需求有很多种，但是在这里我们只关注常见的三种：

1.      抗原像性（有些时候称为“单向性”）:给出一些输出Y=H（X），找到一个令H(X)=Y的输入X是一件很耗时间的事。（当然，对此有很多注意事项，但理想情况下，这种攻击需要的时间可以媲美从任何东西中提取X的暴力穷举。）

 

2.      抗第二原像性:它和抗原像性有一点不同，给出一个输入X，攻击者很难找到另外一个输入X’，使得H(X)=H(X’)。

 

3.      抗碰撞性:很难找到两个值X1，X2,使得H(X1)=H(X2)。另外需要注意的是，因为攻击者可以自由选择任意两条消息，所以这一点其实是比抗第二原像性更强的假设。

我认为上面提到的hash例子包含所有这些属性。也就是说，还没有人明确提出有效（即使是理论上）的攻击能够破坏这三条中的任意一条。当然了，情况总是会改变的，等到了这一天我们也就会停止使用它了。（后面我们还会讨论未来在量子攻击下的情况）

既然我们的目标是利用hash函数创建签名方案，那么我们简要回顾一下hash函数也是有帮助的。

数字签名方案以公钥为基础，用户用数字签名方案生成一对密钥，分别叫做公钥和私钥。用户保存私钥，并用私钥为任意信息“签名”，“签名”的结果就是生成数字签名。拥有公钥的人可以验证消息及其签名的正确性。

出于安全的考虑，在签名中，我们想要的主要属性就是不可伪造性，或者叫“存在性不可伪造”。这一需求就意味着攻击者不能在你没有签名过的消息上伪造有效的签名。想看更多有关签名安全的证实定义的消息，看这一页。（https://blog.cryptographyengineering.com/euf-cma-and-suf-cma/）

Lamport一次性签名

第一个hash签名方案是在1979年由一个名叫LeslieLamport的数学家发明的。Lamport观察到给出简单散列函数，或者说是单向函数，就很可能会生成一个非常强大的签名方案。

这里的强大是假定你只需要签名一条消息，下面我们来详细说一下。

作为讨论，我们假设我们有以下组成部分：一个有256bit输入和256bit输出的hash函数。SHA256就是这种函数的一个非常好的例子。我们也需要一些生成随机比特的方法。

现在我们设想一下我们的目的是签名256比特的消息。为了生成密钥，我们应该做的第一件事就是生成一系列即512个独立的随机比特串。为了方便，我们把这512个比特串分成如下两组：

上面的两个列表（SK0，SK1）表示我们用于签名的密钥。为了生成公钥，我们用函数H(.)对这些随机串进行散列。然后就会生成如下两个列表:

我们现在可以向全世界展示公钥（PK0,PK1）。比如，可以把公钥发送给我们的朋友，把公钥嵌入某个证书，或者把它保存到keybase。

当我们想用自己的密钥签名一个256bit的消息M时，我们要做的第一件事是分解M并把M用单个比特表示：

 

签名算法的其它部分很简单。我们只需要把消息从头到尾处理一遍，根据信息的每个比特的值选择密钥的每个比特。

从i=1到256：如果第i个消息比特Mi=0，我们找出第i个密钥串（ski0）把这个串作为我们签名的一部分并输出。如果消息比特Mi=1，我们从第二个列表中复制合适的串（Ski1）。对每一位消息比特做完以上操作，我们把所有串连接起来。这就组成了签名

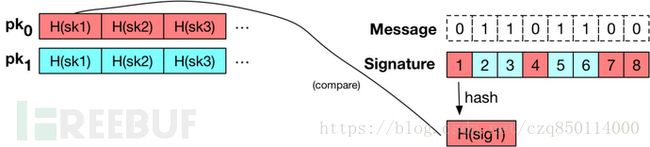
这有一个关于这个程序的说明，在这个例子中密钥和信息长度仅有8bit。需要注意的是，下面每一个涂色的小方格都表示一个256bit的随机串:

 

当一个已经拥有公钥（PK0，PK1）的用户收到消息M和一个签名，他可以很容易地验证这则消息。用s_i代表签名的$i^{th}$部分：对于每一个串，她检查相应的消息比特位Mi并计算哈希值H(si)。如果Mi=0结果就应该和PK0中的元素相匹配。如果Mi=1就说明结果应该和PK1中的元素相匹配。

如果签名中的每一个元素都匹配到公钥中正确的部分，那么这个签名是有效的。关于验证过程这里有一个简短的说明，对于至少一个签名组件的部分：

 

如果你对于Lamport方案的第一印象 是这个方案有点疯狂，那么你的这个想法有一个比特是对的有一个比特是错的。

我们从消极的方面开始讲。首先，我们很容易就会发现Lamport的签名和密钥都很大，而且非常苛刻的是，每一个密钥只能签名一个消息。这样这个方案就变成了“一次性签名”的一个实例。

要理解这一限制，我们来回忆一下，每个Lamport签名都揭示了每个位置上两个可能的键值之一。如果我只签名一条消息，那么这个签名方案运行很流畅。然而，如果我曾经签名每个比特位都不同的的两条消息，那么我就要把这个位置的两个秘钥都分发出来。这就是个问题了。

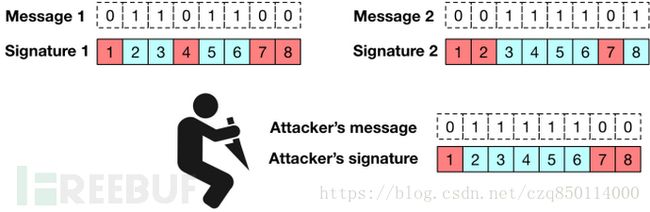
想象一个攻击者在不同的消息上看到两个有效的签名，攻击者可以执行一个简单的“混合和匹配”的伪造攻击，使她能够签名一个我从未签名过的第三条消息。以下是我们的小例子的工作示意图：

攻击者伤害你的程度取决于这些信息有多大差异以及你给攻击者多少信息。但这并不是一个好消息。

总结一下我们对Lamport签名方案的观察，那就是它很简单很快，而且由于各种各样的原因，这个方案并不好。或许我们可以把它做的稍微好一点。

从一次性签名到多次签名：Merkle的基于树的签名

尽管lamport模式是一个好的开始，但是仍然有很大的缺陷，那就是没有办法用一个密钥签名多条消息。Martin Hellman的学生Ralph Merkle受到启发，他很快提出一个非常聪明的方法来解决这个问题。

尽管我不能很准确的复原Melkle的步骤，但是我们还是来看一下能否复原其中一些比较明显的想法。

假设我们的目标是使用Lamport签名签署很多消息，假定这些消息数量为N。最明显的方法就是按原方案生成N个不同的密钥对，然后把所有的公钥连接成一个巨型密钥。（巨型密钥是我自己发明的术语）

如果签名者持有N个密钥组件，那么她现在可以通过每条消息对应一个密钥的方式来签名N条不同的消息。这似乎解决了这一问题，而且也不需要重复使用密钥。

显然这种方法非常浪费时间。

特别是，用这种幼稚的方法，签名N次要求这个签名者分发的一个是正常Lamport公钥N倍的密钥。（她同样需要保存一大堆类似的密钥）。人们会在某个时候对此感到厌倦，而且也许N不会每个都很大。进入Merkle的想法。

Merkle提出一种方法可以保持签名N条不同的消息的能力，而公钥成本没有爆炸性增长。Merkle的方法大概类似这种：

1.      首先生成N个Lamport密钥对。我们可以把他们称为（PK1，SK1）……,(PKn,SKn)。

 

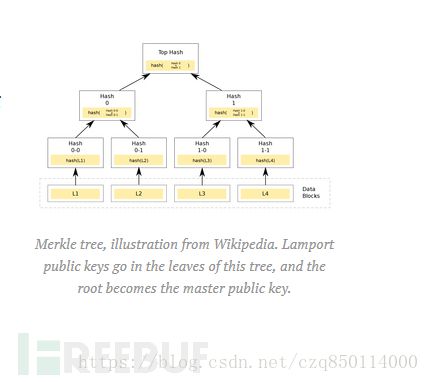
2.      然后，把每一个公钥都放在Merklehash树的叶子节点上（如下所示）,然后计算树的根节点。这个根节点将会成为新的Merkle签名模型的“主”公钥。

 

3.      签名者保留所有的Lamport公钥和私钥用于签名。

 

Merkle树在这里有一个很好的描述（https://en.wikipedia.org/wiki/Merkle_tree）。粗略地说一下就是，它们提供了一种方法，用这种方法可以收集很多不同的值，这样这些值可以由单个“根”散列表示。给出这个散列值，就很容易生成一个元素在hash树中的简单的证明。更何况，这个证明的大小是树上的叶子节点个数的对数。

为了标记第i个消息，签名者仅输出树上的第i个公钥,并用相应Lamport密钥签名消息。然后，她把Lamport签名和相应的Lamport公钥连接起来，并把为他们贴上“Merkle proof”，这表明该特定Lamport公钥包含在由根（整个方案的公钥）识别的树中。然后，她将这整个树作为消息签名发送。

（要验证此表单的签名，验证人只需将该“签名”分解为Lamport签名，Lamport公钥和Merkle Proof。她会根据给定的Lamport公钥验证Lamport签名，并使用Merkle Proof验证 Lamport公共密钥是否真的在树上，有了这三个目标，她可以相信签名是有效的。）

这种方法的缺点是将“签名”的大小增加了两倍以上。然而，该方案的主公钥现在只是一个散列值，这使得这种方法比上面的解决方案更为精确。

作为最终的优化，通过使用密码伪随机数发生器的输出产生各种密钥，密钥数据本身可以被“压缩”，这允许一个密码伪随机数发生器由一个短小的“种子”产生大量的比特（明显是随机的）。

令签名和密钥更高效

Merkle的方法允许许多一次性签名转变成N次签名。然而他的结构仍然需要我们使用一些潜在的类似于Lamport方案的一次性签名。不幸的是Lamport方案的带宽成本[M8] 仍然很高。

这里有两个有助于降低成本的优化方案。第一个方案也是Merkle提出的。我们先分析这个简单一点的技术，主要是因为它有助于我们解释更强大的那个方案。

如果你回忆Lamport的方案，为了签署一个256bit的消息，我们需要一个由512个对应的密钥比特串组成的向量。签名本身是是256个秘密比特串的合集。

但是这里有一个想法：如果我们不签署消息里所有的比特会怎么样呢

进一步解释一下。在Lamport的方案中，无论每一比特消息的值是多少，我们都通过输出一个秘密字符串的方式签名每一个比特消息。如果我们不是既签名消息中的0值又签名1值，而是仅签名消息中的为1的值而会如何？这会把公钥和私钥的大小砍掉一半，因为我们跳过了整个SK0列表。

现在在密钥中只有一个单一比特串列表  ,在消息的每个Mi=1的比特位,我们会输出一个串ski。在每一个Mi=0的位置我们会输出..zilch(这也会减少签名的大小，因为许多消息包含了一堆零比特，而这些信息现在就不会给我们带来任何损失！)。

这种方法有一个非常明显的问题：非常不安全。所以不要执行这个方案！

举个例子，一个攻击者观察到一个被签名的消息，以“1111…..”开头，而且她想要在不破坏签名的情况下编辑这条消息，从而让这条消息显示为“0000……”。要想实现这个目标，她需要做的就是删除这个签名的几个组件。总之，把一个0比特变成一个1比特很困难，但是反过来做却很容易。

但是这有一个解决办法，而且相当的简洁。

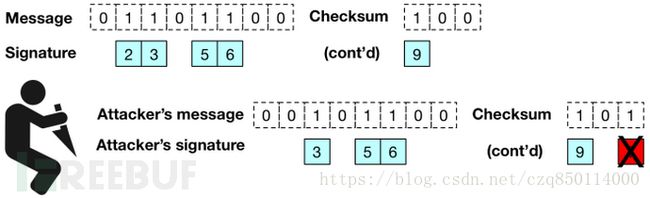
你要知道，当我们不能阻止一个攻击者把0比特变成1比特时，我们可以catch他们。为了做到这一点，我们对消息进行简单的“校验和”，然后签名原始消息和校验和。签名验证器必须在两个值上验证整个签名，并确保接收到的校验和正确。

我们使用的校验和很简单：它由一个简单的二进制整数组成，它代表原始消息中的零比特的数量

如果攻击者试图修改消息的内容（不包括校验和）以便将某些1比特变成0比特，签名方案不会阻止她。但是这种攻击会增加消息中0比特的数量。这立即使校验和失效，然后验证者会拒绝签名。

当然，一个聪明的攻击者也可能会试图混淆校验和（它也与消息一起被签名），以便通过增加校验和的整数值来“修复它”。但是很关键的一点是，由于校验和是一个二进制整数，为了增加校验和的值，她总是需要将校验和的某个零位变成一位。但是由于校验码也是签名的，并且签名方案阻止了这种改变，攻击者无处可去。

tu

（如果你在家中最终，这会增加被签名的’消息’的大小，在我们的256位消息的例子中，校验和需要额外的8位和相应的签名成本，但是如果消息有很多零位，缩小签名大小通常仍然是一个胜利。）

Winternitz：用时间换空间

上面的手段把公钥的大小减少了一半，并把签名的的大小减小到一个很小的量。这很好，但是还算不上真正的革新。因为它仍然给出了数千位长度的密钥和的签名。

如果我们能进一步让这些数字变小，那就太好了。

我们即将讨论的最后一个优化是Robot Winternitz提出的，是对Merkle技术的深度优化。在实际使用中，以增加签名和验证的时间为代价，能够把签名和公钥的大小降低4-8倍，。

Winternitz的想法是一种名叫“时空权衡”的技术的一个例子。这一术语指的是一系列解决方案，在这些解决方案中以增加计算时间为代价减少空间。解释下面的问题，有助于理解Winternitz的方法，：

如果我们在对消息进行签名时，把我们的消息看做是由大字节符号字母编码的，而不是由比特组成的，又会如何？例如，如果我们一次签名4比特呢？如果是8比特呢？

在Lamport的原始方案中，我们有两个作为签名密钥（或者叫公钥）的比特串列表。一个用于签名消息中的0比特，一个用于签名消息中的1比特。

现在，如果我们说，我们想加载字节而不是比特。一个非常明显的想法就是把密钥列表的数量从两个列表增加至256个列表。每一个列表对应一个可能出现的消息字节。签名者一次就可以处理消息的一个字节，并从更大的菜单中摘出关键值。

不幸的是，这种解决方案真的是太麻烦了。它以把公钥和私钥的数量增加到256个[ 为代价，把签名的大小缩小了8倍。如果这个公钥可以用于许多签名，即使这种方法是可行的，但是当涉及到密钥重复使用时这种方法就没用了，这个“字节签名版的Lamport”跟原始的Lamport签名一样会受到很多限制。

以上所有问题都把我们引向Winternitz的设想。

由于存储和区分256个完全随机的列表实在是太难了，如果我们只在需要的时候通过程序生成这些列表会怎么样呢?

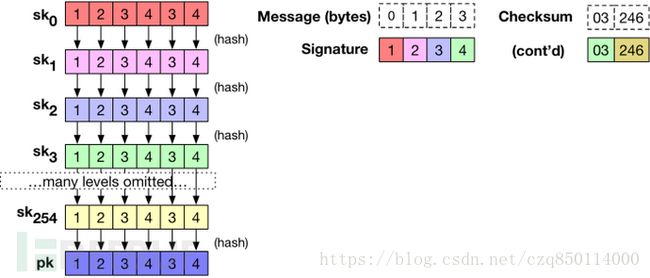
Winternitz的想法是为我们的初始密钥生成一个随机种子列表，,为了为密钥导出下一个列表，他建议用哈希函数H()处理初始密钥上的每一个元素，而不是生成另外一个随机列表，列表如下：

类似得，某人可以再次对sk1列表使用这个哈希函数，从而得到下一个列表 :

以此类推，重复254次就可以得到剩下的列表。

我们现在只需要存储一个单一的密钥列表SK0,而且我们仅仅通过调用哈希函数就可以分发其他的列表。

但是，公钥该怎么办呢？这就是Winternitz聪明的地方了！

Winternitz提出通过把哈希函数再次作用于最后一个密钥列表来分发公钥，这会生成一个单一的公钥列表pk。这一方式的优点在于每一个得到密钥的人都可以通过多次hash检查公钥。

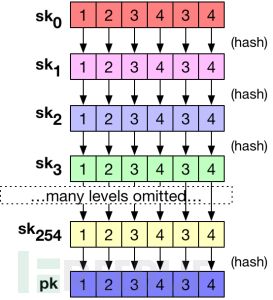
生成密钥的完整步骤在下面做了说明：

为了签名消息的第一个字节，我们需要从适当的列表中选取一个值。比方说，如果这个消息字节是“0”，我们会从签名的sk0中输出一个值。如果这个消息字节是“20”,我们会从sk20中输出一个值。对于具有最大值255的字节，没关系：我们可以输出一个空字符串，或者我们会输出适当的pk元素。

同样也要注意，事实上我们并不是真的需要存储每一个私钥列表。我们可以从原始列表sk0中获得需要的值。验证者只是持有公钥向量并只需要向前散列适当的次数（取决于消息的字节数），来确定结果是否等价于公钥的适当组件。

就像前面讨论过的Merkle优化，前面提到的方案也有明显的漏洞。由于密钥是相关的，任意看到已经签名“0”的消息的人都能轻易的把消息相应的字节修改为“1”。并更新匹配的签名。事实上，攻击者可以在消息中增加任意字节的值。如果不检查这个功能，就可能带来非常强大的伪造攻击。

这个问题的解决方案和我们在上面讨论的非常相似。为了防止攻击者模仿签名，签名者计算并签名一个初始消息字节的校验和。设计这个校验和的目的是防止攻击者增加字节后校验和不失效的情况。

毫无疑问，获得校验和非常重要 。哪怕只是搞砸了一点点，你也可能会发生一些非常不好的事情。如果在生产系统中部署这些签名，这会让人非常讨厌。

如下面这个图片所示，一个Winternitz方案的4字节的小例子就是这样的：

 

hash签名方案擅长什么呢？

由于在整个讨论过程中，我们主要讨论如何进行hash签名，而不是为什么使用hash签名。是我们解决这个问题的时候了。这些奇怪的结构有什么意义呢？

一个支持hash签名的早期论点是：他们明显很快也很简单。由于他们只需要对哈希函数和一些数据复制进行评估，单纯从计算成本的角度来看他们与类似ECDSA和RSA的方案竞争激烈。可以假设这对轻量级的设备很重要。当然，这种效率在带宽效率上是一个巨大的权衡。

然而， 最近逐渐注意到hash签名结构还有更复杂的原因。它源于这样一个事实即所有的公钥密码都将被破解。

更具体地说：即将到来的量子计算机即将对几乎所有的签名算法安全产生巨大的影响，从RSA到ECDSA甚至其他的算法。这是基于这样一个事实即Shor算法提供的多项式时间算法解决了离散对数问题和因式分解问题，这些问题可能会使大部分方案变得不安全。

大多数hash签名的实现不易受Shor算法的攻击。当然，这并不意味着他们完全不受量子计算机的影响。对散列函数最有效的通用量子攻击是一种基于Grover算法的搜索技术，这种算法降低了Hash函数的有效安全性。但是，有效安全性的降低远不及Shor算法严重（它的范围在平方根与立方根之间），因此可以通过增加内部容量和哈希函数的输出大小来保持安全。为了提供抵御这种攻击，开发了类似SHA3的具有很大的摘要值的哈希函数。

所以最起码在理论上，hash签名算法是很有趣的，因为目前来说，它为我们提供了一道抵御未来量子计算机的防线。

未来呢？

注意到目前为止，我只讨论了一些“传统的”哈希签名方案。以上我描述的所有方案都是在20世纪70年代或者20世纪80年代早期发明的。但是这些方案很难让我们了解现代的技术。这很难把我们带到现代。

在我写完这篇文章的初稿以后，有些人要求提供关于该领域最新的参考在这里我不可能提供一个详细的列表，但是让我们描述一下其他人最近提出的一些想法。

无状态签名。一个上述所有签名方案的限制是他们要求签名者在签名之间保持同一个状态。在一次性签名的例子中推理是显而易见的：你要避免对任意密钥进行重复使用。但是即使在多次Merkle签名中，你需要记住你在使用哪个公钥叶子结点，从而避免二次使用某个叶子节点。更糟糕的是，Merkle方案要求签名者提前构造所有的密钥对，所以签名的总数是有限的。

在20世纪80年代，OdedGoldreich指出可以在没有这一限制的情况下构建签名。这个想法如下：一个人可以构建一个一次性公钥的短小“证书树”,而不是提前生成所有的签名。这些密钥中的任意一个都可以用来签名这个树低层次的一次性公钥，诸如此类。所有的私钥都是由单个种子生成的，这就意味着在生成密钥时，不需要一个完整的证书树存在，而是可以在生成新密钥时，按需建立。每一个签名包含一个签名的“证书链接”而且公钥从根开始，并转到树底部的真实签名密钥对。

这一技术允许构建有很多签名密钥的树。如果我们随机选取一个签名密钥，这允许我们构建很多一次性公钥，然后很大可能相同签名不会被二次使用。当然，这是直觉。对于这一思想的高度优化和具体实例化，可以看Bernstein推荐的SPHINGS。现实中的SPHINCS-256实例通常给出大约41KB的签名。

Picnic：后量子零知识签名。Picnic在另一个完全不同的方向上。Picnic基于一个叫做ZKBoo的新的非交互式零知识证明系统。ZKBoo是一个在基于一种叫做“MPC in the head”的技术上的新的ZK证明系统，证明人在这个系统上用证明着自身通过多方计算计算一个函数。这个太复杂的，无法解释的更详细，但是最终的结果时，只能用哈希函数证明结构的复杂性。

他的长处和短处是Picnic与相似的ZK证明系统提供了构建来自HASH函数的签名的第二个方向。这些签名的代价仍然很大，大约有几百KB。但是这门技术在未来的改进能够大幅度减小签名的大小。

后记：无聊的安全细节

如果你回顾一下这篇文章前面的内容，会发现我花了一些时间描述hash函数的安全性。这不仅仅是为了作秀。你知道，hash签名方案的安全性在很大程度上取决于哈希函数提供的属性。

（言下之意就是，hash签名的不安全性决取于攻击者设法突破了hash函数的哪一个属性。）

大部分讨论散列签名的原稿，会展示散列函数抗原像性的安全参数。

大多数讨论hash签名的原创论文，通常会展示有关哈希函数抗原相性有关的安全论据。乍一看，这似乎很简单。我们以Lamport签名为例分析一下。给定一个公钥的元素pk ₁ º=H(sk ₁ º)，一个能够计算哈希原像的攻击者可以很轻松的为签名的该组件恢复有效密钥。这种攻击显然会使这种方案变得不安全。

然而，这个论点仅仅考虑了攻击者只拥有公钥但还没有见到有效签名的情况。在下面这种情况下，攻击者拥有的信息稍微多一点。他们现在有公钥和一部分私钥：pk ₁ º=H(sk ₁ º)以及$latex sk^{0}_1$。如果这样的攻击者可以找到公钥pk ₁ º的第二原像，他不能给另一个消息签名。但是她生成了一个新的签名。在签名安全的强定义中（suf-cma）这实际上是一个有效的攻击。所以suf-cma需要更强的抗第二原像性。

当然了，在hash签名方案的实际应用中，出现了最后一个问题。你会注意到上面的描述是假设我们将要签名一个256bit的消息。而问题在于，在现实应用中，许多消息不止256bit。所以，很多人用hash函数H（）先把消息散列为D=H(M),然后对散列后的结果D进行签名，而不是对消息本身进行签名。

这就导致了对最终方案的最后一重攻击，由于该方案的存在性不可伪造依赖于哈希函数的抗碰撞性 。一个攻击者能够找到两条不同的消息，令M1！=M2而H(M1)=H(M2)，现在可以找到对不同的两条消息均有效的签名。这就导致EUF-CMA安全性的一个微小的突破