Course 4-Convolutional Neural Networks--Week 1
终于~吴老大出了深度学习的第四课-卷积神经网络,赶紧一睹为快~
本周的课程包括卷积神经网路的一些基础知识:边缘检测、图像边的填充padding、滑动步长stride、3D卷积操作、单层卷积网络、池化层、卷积神经网络例子以及为什么需要卷积。
1.1 Computer Vision计算机视觉
计算机视觉领域的问题:
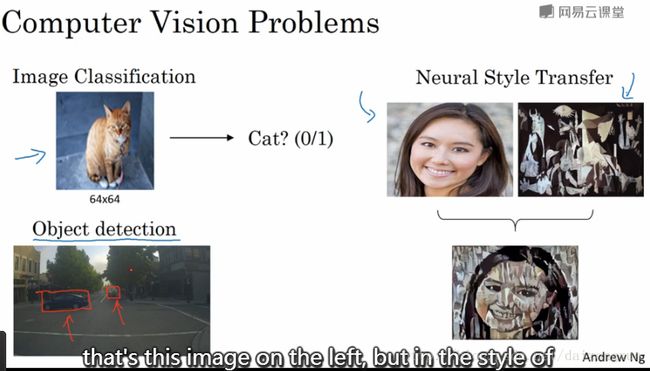
- 图像分类(有时也称为图像识别)
- 目标检测(找到目标在图像中的位置,目标数量不定)
- neural style transfer(需要content image和style image,下图里的content image是吴恩达的老婆哦~美腻啊!)。
计算机视觉的挑战之一是:输入图像可能非常大。比如1000*1000的彩色图像,总共有3百万的参数,如果第一个隐藏层有1000个隐藏单元,采用全连接的话,这个时候权重参数矩阵就有30亿个元素。这样的参数量就太大了。
1.2 Edge detection example边缘检测例子
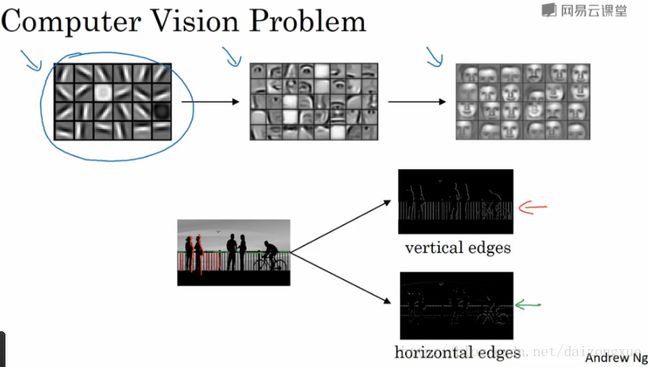
卷积操作是卷积神经网络的基础模块之一,使用边缘检测作为引出的例子。本节中,你将学习卷积是怎么工作的。之前的视频中已经讨论了神经网络的前几层是如何进行边缘检测的,随后的几层是如何检测目标的部分信息,最后的几层是如何检测物体的。如下图所示。本节讲述神经网络的前几层是如何进行特征提取的。
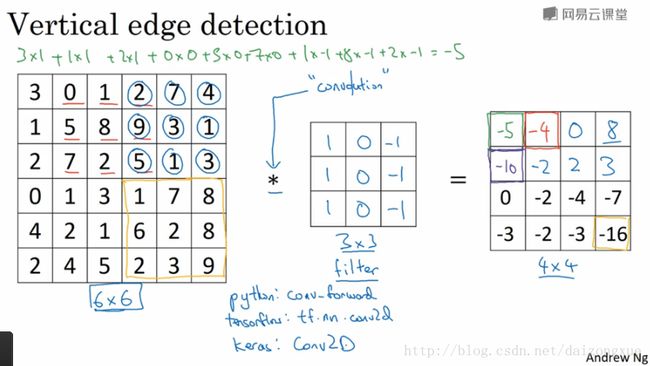
边缘检测实例,以及卷积操作在不同框架下的实现函数如下图所示。
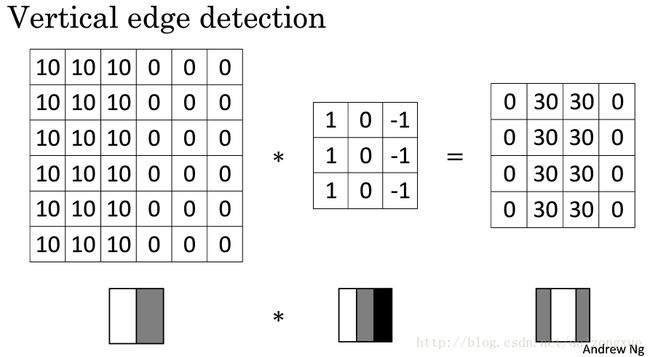
为什么上述操作可以实现竖直方向的边缘检测呢?为了说明,我们使用如下图所示的简化图像。当滤波器(也可称为核,kernel)在图像区域滑动时,产生的结果图像如右边的矩形所示,即把竖直方向的边缘检测了出来。
1.3 more edge detection
本小节将讨论正、负边缘的区别,即从亮到暗和从暗到亮的区别。还会讨论如何自动学习边缘特征。如下图所示:
- 第一幅图的左边为亮区域、右边为暗区域,滤波器的左边为亮区域、右边为暗区域,得到的边缘检测结果为正值;
- 第二幅图的左边为暗区域、右边为亮区域,滤波器的亮暗区域不变,滤波的边缘结果由正值变为负值。
边缘检测结果的正负可以表明,图像是从亮区域过渡到暗区域还是从暗区域过渡到亮区域的。如果不太care这个过渡细节的话,直接取滤波结果的绝对值即可。
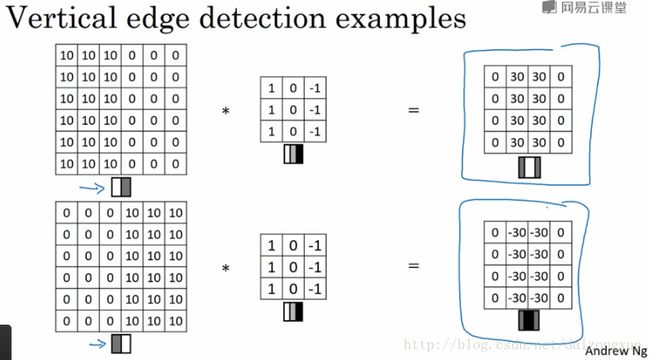
下图给出了一个更复杂的例子,其滤波结果如图所示。
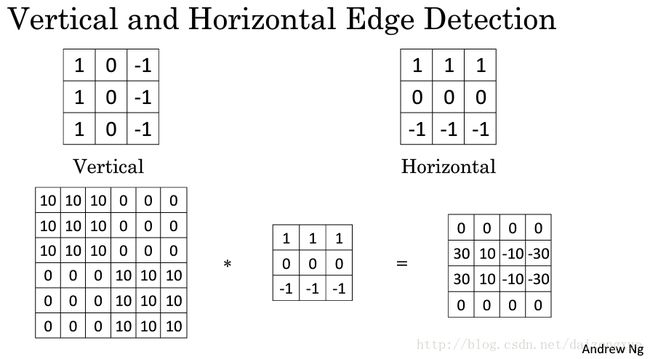
总结一下,不同的滤波器使我们可以发现竖直和水平的边缘。同样是竖直边缘检测,当我们给滤波器分配不同的参数,得到的结果也不尽相同。当我们处理复杂图像时,或许我们可以无需刻意指定滤波器的参数,我们可以通过后向传播算法学习它们,将这9个数作为参数。如下图所示。

除了水平边缘和竖直边缘外,我们通过后向传播还可以学习其他方向(如45°、70°、73°等等)的边缘检测滤波器参数,并且学习到的滤波器比手工设计的滤波器更具有鲁棒性。
1.4 padding填充
对于上一小节的例子,当图像大小是6*6,滤波器大小是3*3时,滤波结果图像是4*4,这样我们的图像就从6*6变成了4*4,当图像多经过几个滤波器后,它可能变得越来越小,maybe 1*1~ 另外一个负面影响是,对于一幅图像,四个角和上下左右四条边上的像素被使用的次数少于中间像素,因此,我们丢失了很多图像四周的信息。为了解决shrinking output和throwing away a lot of information from the edges of the image这两个问题,我们可以通过填充图像边缘来保持图像大小不变。

为了方便,我们填充0,并且滤波器的size都是奇数。在实现卷积时,我们有“valid”和“same”两种选择,分别对应no padding和padding。

1.5 strided convolutions
本小节讨论卷积步长问题。之前滤波器移动时,步长都为1,那么当步长为2时,情况又是什么样呢?如下图所示,7*7的图像,滤波结果为3*3大小。
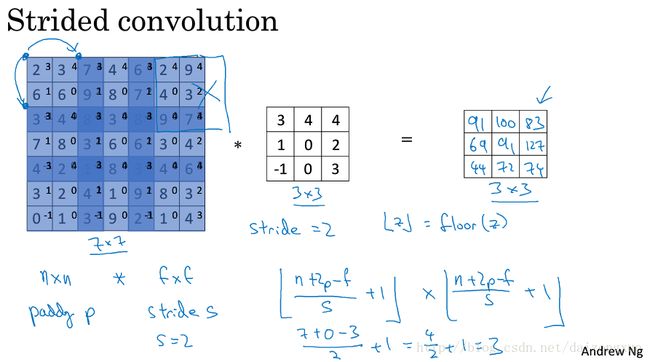
下图给出了,当图像的size、filter的size、padding p、stride s都给定时,滤波结果图像大小的计算公式

在继续之前,有必要区别一下convolution和cross correlation(互相关)。真正的卷积操作要对filter进行水平和垂直方向的翻转,如下图所示,然后进行对应元素相乘再相加的操作,而在深度学习中,为了方便,我们没有对滤波器进行翻转,而是直接进行对应元素的相乘再相加,这种操作实际上应该叫做cross correlation。但是大多数深度学习文献都称之为卷积操作,因此我们也就习惯性的称其为卷积。另外一点,在信号处理等领域,滤波器翻转是为了满足卷积的结合律,如下图所示。但是,对于深度学习来说,我们并不关注这一点性质,因此,忽略两次翻转能为我们的实现带来简化,而神经网络能一样工作的很好。
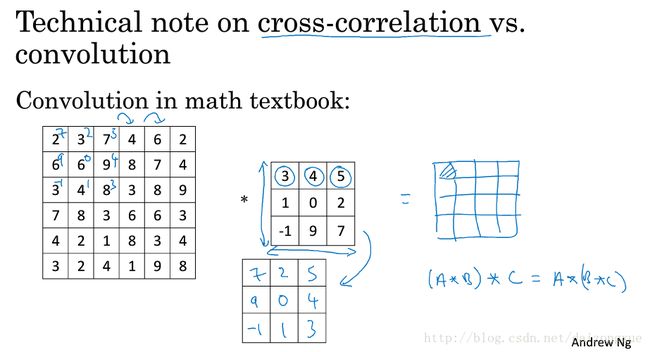
目前,卷积的对象都是二维矩阵,接下来将说明如何对三维的立方体卷积。
1.6 Convolutions over volumes
前面已经说明了卷积是如何在2D图像上工作的,下面来说明卷积在3D立方体上式如何工作的。如下图所示,以一幅具有RGB 3通道的彩色图像为例,为了获得边缘或其他一些基本特征,我们不再使用之前的二维滤波器,与3通道的彩色图像相对应的,我们使用3D的滤波器,使滤波器的3层分别对应R、G、B三个通道。如图所示,三个维度分别称之为height、width、#channels。同时,图像的#channels必须和filter的#channels相等。最终,得到一幅具有一个通道的图像。
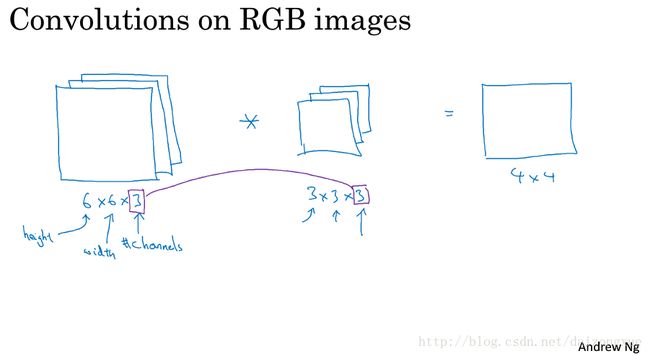
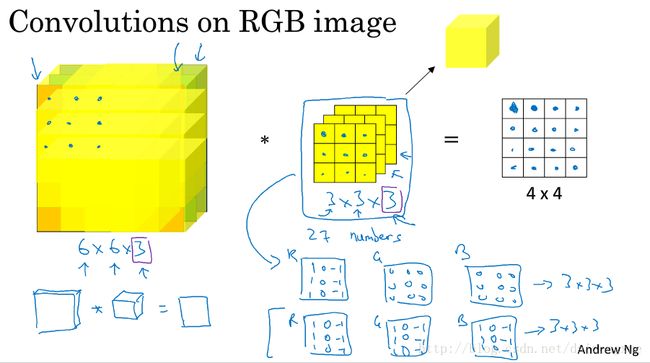
下面换一幅好看一点的图接着说明。有时为了简化,也会将3D filter化成右上角那个黄色的立方体。为了计算该卷积操作的输出,将这个3*3*3的滤波器放在图像的左上角,如下图所示。这个3*3*3的滤波器共有27个参数,我们要做的就是将滤波器的参数与对应图像上的像素值相乘,最后将这些乘积相加得到输出的第一个数值。如下图所示。

接下来,我们依次计算输出的其他数值。每次将filter移动一格,计算输出结果。这样做到底是什么意思呢?比如说我们要检测图像中R通道的边缘,下图写出了filter的R、G、B三层的参数,我们将这三个2Dfilter堆叠起来就形成了3*3*3的filter,那么这个filter就可以检测到R通道中的竖直边缘。如果我们不在意竖直边缘在哪个颜色通道中,那么,就可以使用图中下方所示的filter,这样的filter就能检测任何颜色中的竖直边缘。当filter中的参数不同时,就能获得不同的特征检测器。习惯性的,在计算机视觉领域,当输入的height、width、#channels都确定时,我们定义的filter与输入具有不同的height和width,但具有相同的#channels。
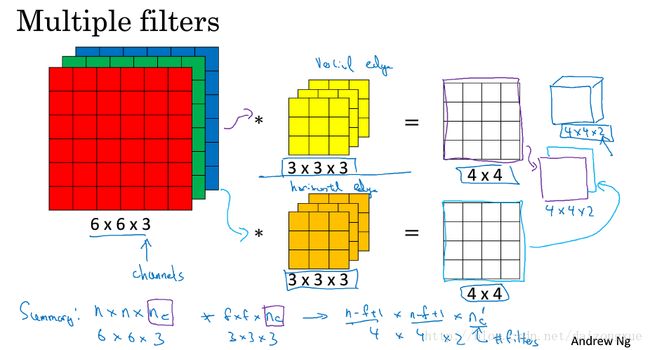
在构建卷积神经网络时,还有一个关键点,那就是,如果我们不只想检测竖直方向的边缘该怎么办?如果我们想检测竖直和水平方向的边缘该怎么办?或者45°、70度方向的边缘该怎么办?换句话说,如果我们想同时使用多个filters应该怎么办?
如下图所示,假设第一个3*3*3的filter是检测竖直边缘的,通过这个filter,我们得到一个4*4的输出;第二个3*3*3的filter是检测水平边缘的,通过这个filter,我们仍得到一个4*4的的输出,将这两个输出堆叠在一起,就得到了一个4*4*2的输出。总结一下,如下图下方所示,输出的#channels与使用的滤波器个数相等。
1.7 one layer of a convolutional network
下面通过一个例子说明如何构建一个单层的卷积神经网络。正如前面已经说明的,3D filter 对 3通道的图像做卷积后,得到一个4*4的结果,我们给这个结果加上一个实数bias,Python会将这个bias 广播到矩阵的每一个元素上,然后再经过一个非线性函数,如relu,得到非线性输出,最后,将所有非线性输出堆叠。这样一个从6*6*3到4*4*2的计算过程就是一个卷积神经网络的一层。前向传播的计算过程如下图左下角所示,3通道的图像就是输入,这里的filters就像公式中的W。下图展现的就是从 a[0] 到 a[1] 的计算过程。

接下来做一个练习检验一下是否已经理解上面的内容
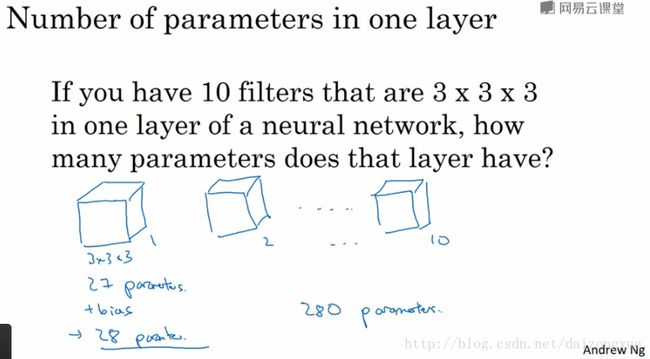
值得注意的是,无论输入图像有多大,我们需要的参数个数始终都是280。我们可以使用这10个filters进行各种各样的特征检测。最后,总结一下标记,如下图所示,根据之前的说明都可以计算或推出。需要提一下的是,如果使用向量化实现时,如 batch gradient descent 或 mini-batch gradient descent,那么这时输出 A[l] 就是4D的tensor了,多了一个样本个数的维度。权重向量也是4D的,各个维度的维数如下图所示。

1.8 A simple convolution network example
上一节已经了解到如何构建卷积神经网络的一层,本节介绍如何构建一个深度卷积神经网络。
假设有一幅39*39*3的图像,我们要做图像分类或识别的工作,首先用10个3*3*3的filters做stride=1,no padding的卷积,得到37*37*10的中间结果;接着继续用20个5*5*10的filters做stride=2,no padding的卷积,得到17*17*20的中间结果;接着继续用40个5*5*10的filters做stride=2,no padding的卷积,得到7*7*40的中间结果;最后,我们将这个结构flatten或者unroll,得到一个长度为1960的一维向量,然后使用logistic或者softmax进行预测。设计卷积神经网络的大多数工作是选择filter size、stride、padding、#filters这些超参数。后续的课程中将给出一些guidelines on how to make these choices。对于这样一个网络,图像的height和width会越来越小,而#channels通常会上升。

在一个典型的卷积神经网络中,有三种类型的layers,分别如下图所示。

1.9 Pooling layers
除了卷积层外,ConvNets还经常使用pooling layers(池化层)to reduce the size of their representation to speed up computation 以及使检测到的特征更加鲁棒。
下面举个池化层的例子,并说明为什么要这样做。假设我们使用的是max pooling,如下图所示,每个2*2的区域输出其最大的那个像素值。可以理解为,使用filter进行特征检测后,如果在某一区域有特征,那么特征所在的像素就比较大,我们使用max pooling就可以将这个特征保持下来;如果在某一区域没有特征,那么使用max pooling后得到的值仍然很小。Maybe that’s the intuition behind max pooling. 人们广泛使用max pooling的原因是它的确能工作的很好。max pooling一个有趣的性质是:它有一个超参数集合但是没有可学习的参数,即没有梯度下降法所学的参数。一旦固定了 f 和 s ,那么这就是个固定的计算,梯度下降不会改变任何东西。
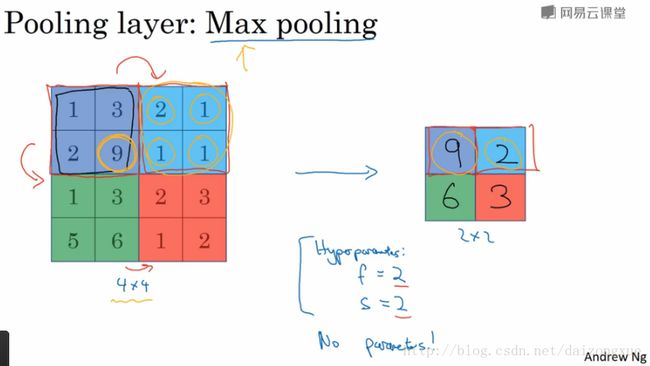
下面举一个不同参数的max pooling例子。超参数 f 和 s 的取值如下图所示。如果输入是3D数组,那么,输出也是3D的数组,因为池化操作是对图像的每个channel独立进行的,因此,池化操作不改变图像的#channels。

以上是max pooling,还有一种不常使用的pooling类型——average pooling。在做pooling操作时,我们不用max而是用average,如下图所示。近些年,我们使用max pooling的频率超过average pooling。但只有一个例外,有时,当神经网络很深的时候,你可能要使用average pooling to collapse implementation from 7*7*1000 to 1*1*1000。

最后,总结一下,池化操作的超参数有filter size: f、stride: s以及是要用max pooling 还是 average pooling,如果你乐意,还可以加入padding,但是这样非常非常少见。大多数情况下,max pooling都不会进行任何padding。常见的filter size和stride如下图所示。对于一个池化层,输入输出的size如下图有部分所示。有一点需要注意的是:池化层没有参数需要学习!

现在已经学习了卷积层和池化层,接下来将实现一个较为复杂的ConvNet。
1.10 Convolutional neural network example
此处的ConvNet是受LeNet-5的启发,但并不是LeNet-5。
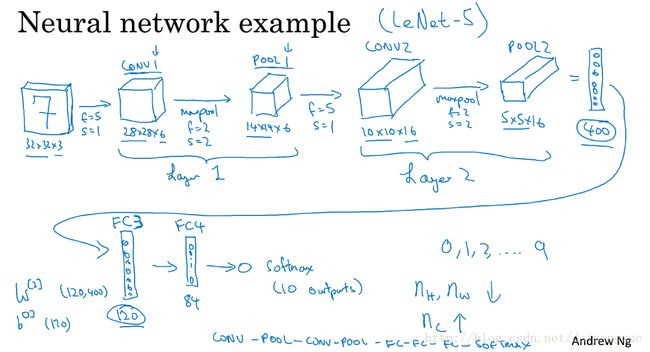
假设我们的输入图像的大小为32*32*3,第一层的超参数为f=5,s=1,no padding,#filters=6,那么第一层的输出就是28*28*6,我们称这一层为CONV1。应用6个filters,然后加上bias,经过非线性函数后,得到了输出。接下来应用pooling layer,此处使用max pooling,超参数为f = 2,s = 2, no padding,那么这一层的输出就是14*14*6,并称这一层为POOL1。当人们计算神经网络的层数的时候,通常只计算那些有权重(即参数)的layers,由于pooling layer没有权重,只有几个超参数,因此,此处将CONV1和POOL1合起来称为Layer 1。Layer 2的计算如下图中所画出的。POOL 2的输出size为5*5*16,将其flatten为一个长度为400的一维向量,接一个全连接层,输出结果再接一个全连接层,最终接一个softmax layer。这个网络含有很多超参数,随后,将给出一些有关于如何选取超参数的建议。其中一条guideline 就是不要设置自己的超参数,而是查看文献,看文献中的超参数是怎么设置的,选择那些能工作的很好的超参数。
下周将会更多的讨论这一点。但现在,需要知道的是,当网络越来越深,通常情况下, nH 和 nW 会越来越小,而 nC 会增加。另外一个在神经网络中很普遍的模式就是:一个或多个卷积层后接一个池化层,然后又是一个或多个卷积层后接一个池化层,反复几次后,再接少数几个全连接层,最后跟一个maybe softmax。
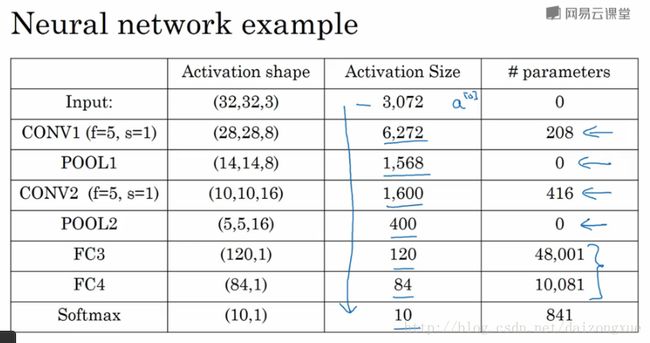
最后,我们回顾一些神经网络的细节,如下图所示。其中,池化层都是没有参数的,activation size随着层次的加深不断变小,如果它变小的过快对性能并不好。
1.11 Why convolutions?
本小节说明下为什么卷积层在神经网络中如此有用,最后再来说一下如何将这些层组合起来形成一个有监督的ConvNet
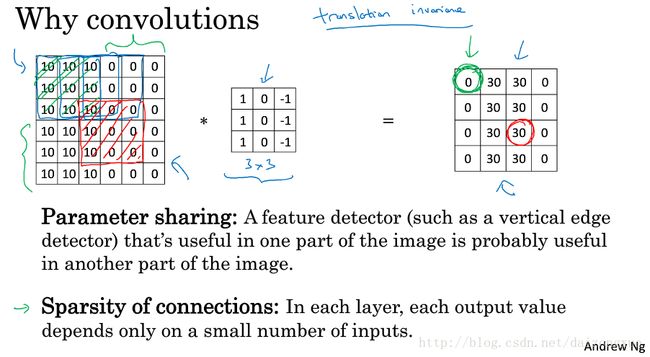
相较于使用全连接网络,卷积层的两个主要优势是:权值共享和局部连接。这样不仅网络训练的参数少了,还能有效防止过拟合。局部连接使卷积神经网络具有平移不变性。
以下图为例,假设输入图像大小为32*32*3(输入神经元为3072个),当卷积层超参数f = 5,#filters = 6时,卷积结果为28*28*6(神经元为4704个)。假如我们使用图中下方的全连接,则权重参数大约需要14 million(3072*4704),而我们使用卷积层的后,则总共只需要 (5∗5+1)∗6=156 个参数,非常小的参数量!

卷积层的参数之所以这么少,主要就是前面说的两个优势:参数共享和局部连接。
最后,我们将卷积层、全连接层等都放在一起,看看怎样训练这样一个网络,如下图所示的ConvNet由若干卷积层和全连接层组成,每一层都有不同的W和b,同样的,我们有一个和之前课程中相同的代价函数 J ,然后运用梯度下降、momentum、RMS prop、Adam等优化方法来最小化代价函数.

本周的内容就这么多,之前也提过,ConvNet中有很多超参数,下周将介绍一些最有效的ConvNets,将会让我们有一种直觉,明白哪种类型的神经网络是有效的。