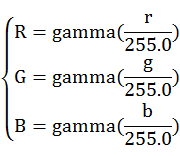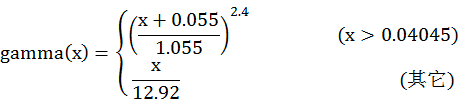RGB与LAB优化互转
转自博客:http://blog.csdn.net/shamaozi/article/details/6221029
虽然若干年前就看过了关于色彩空间的介绍,但是直到今天才自己动手写代码做这件事情。虽然网络上已经有很多现成的例子,但是一则仅仅适用于浮点型的数据,另一方面,在实现上也有一些尚可优化之处。
色彩模型除了最常见的RGB以外,还有HSB、YCbCr、XYZ、Lab等。HSB一般仅仅作为图像处理过程中的临时模式,YCbCr常常用于图像的压缩处理,而XYZ则严格按照人眼对光信号的敏感度进行分布。
这里将要稍作讨论的便是Lab模型。网络上诸多的介绍都说Lab是基于XYZ的,故人们一般也只能找到XYZ和Lab之间的转换,而RGB到Lab的转换只能使用XYZ作为中间模式间接进行。可惜的是,这种现状源于误解。而在图像处理软件中(比如Photoshop),往往采用一个更为简单的算法。
我们可以先观察RGB到XYZ的转换:
[X,Y,Z] = [M] * [R,G,B]
其中M为一3x3矩阵:
[M] = [0.4125, 0.3576, 0.1805;
0.2126, 0.7152, 0.0722;
0.0193, 0.1192, 0.9505],
RGB是经过Gamma校正的色彩分量:R=g(r),G=g(g),B=g(b)。
其中rgb为原始的色彩分量。
g是Gamma校正函数:
当 x < 0.018 时,g(x) = 4.5318 * x
当 x >= 0.018 时,g(x) = 1.099 * d^0.45 - 0.099
rgb以及RGB的取值范围则均为[0,1)。计算完成后,XYZ的取值范围则有所变化,分别是:[0, 0.9506),[0, 1),[0, 1.0890)。
以及XYZ到Lab的转换:
L = 116 * f(Y1) - 16
a = 500 * (f(X1) - f(Y1))
b = 200 * (f(Y1) - f(Z1))
其中f是一个类似Gamma函数的校正函数:
当 x > 0.008856 时,f(x) = x^(1/3)
当 x <= 0.008856 时,f(x) = ( 7.787 * x ) + ( 16 / 116 )
X1、Y1、Z1分别是线性归一化之后的XYZ值,也就是说,它们的取值范围都是[0, 1)。此外,函数f的值域也和自变量一样都是[0, 1)。
计算完成后,L的取值范围[0, 100),而a和b则约为[-169, +169)和[-160, +160)。
在观察这些貌似复杂的变换之前,我们必须确定的一个假设是:在图像处理软件中,非RGB色彩数据的绝对值并不重要,重要的是他们能够尽可能准确的还原成RGB图像以显示在屏幕等相关设备上。这个假设是我们的简化得以成立的理由。
上面的从XYZ到Lab的转换乍一看起来很奇怪,但若是仔细观察,不难发现L与Y1只是一个简单的同区间映射关系,这个映射其实可有可无(如果进行了映射反而必定导致色阶丢失)。
这样,我们取得的第一个简化是:L = Y1。
接下来接着看a和b的映射过程。大家不难发现,a和b其实是一个色差信号(跟Cb和Cr的性质差不多)。至于它们的转换系数500和200,大家可以完全忘记,因为他们的值域并不符合8位整数值的表达需要。我们将会稍后计算出合适的因数,使得a和b都处在[0, 255]的范围内。
因为XYZ必须归一化转为X1Y1Z1,那么我们其实可以在转换矩阵M中作出这个修改,令每行乘以一个系数以使得每行各数之和为1:
[M1] = [0.4339, 0.3762 0.1899;
0.2126, 0.7152, 0.0722;
0.0177, 0.1095, 0.8728]
于是乎,我们得出一个半成品:
L = Y1 = 0.2126 * R + 0.7152 * G + 0.0722 * B
a = Fa * (X1 - Y1) + Da
b = Fb * (Y1 - Z1) + Db
其中的Fx是调整值域用的系数,Dx是一个正数,用来消除a和b的负值。Fx和Dx的选取必须令a和b满足值域在[0, 255]上的分布。
接下来我们来确定Fx和Dx的值。通过M1我们很容易计算出X1-Y1的值域(极端情况)为[-86.784, +86.784),而Y1-Z1的值域则为[-204.9536, +204.9536)。于是乎,Fa的值为1.4749,Fb的值为0.6245;Da和Db则都是128。
这时,代入M1有:
L = Y1 = 0.2126 * R + 0.7152 * G + 0.0722 * B
a = 1.4749 * (0.2213 * R - 0.3390 * G + 0.1177 * B) + 128
b = 0.6245 * (0.1949 * R + 0.6057 * G - 0.8006 * B) + 128
其中RGB和Lab的取值范围都是[0,255]。
最后的一点工作是算法的优化。我们可以将这个方程组转换成常整数乘法与移位的方式(相当于使用定点数)。为了方便阅读,我仍然将移位写为除法。
所以我们的最终结果为:
L = Y1 = (13933 * R + 46871 * G + 4732 * B) div 2^16
a = 377 * (14503 * R - 22218 * G + 7714 * B) div 2^24 + 128
b = 160 * (12773 * R + 39695 * G - 52468 * B) div 2^24 + 128
至于逆变换则可以用类似的方法推导出来:
设L1=L,a1=(a-128)*174,b1=(b-128)*410,有:
R = L1 + (a1 * 100922 + b1 * 17790) div 2^23
G = L1 - (a1 * 30176 + b1 * 1481) div 2^23
B = L1 + (a1 * 1740 - b1 * 37719) div 2^23
其中RGB和Lab的取值范围都是[0,255],再经过逆Gamma函数取得原始的rgb
以上的算法在Delphi中编译通过。经测试,运算得出的直方图与图片观感和我手头的Photoshop CS的结果非常相似,但也有一些幅度上的差别,且容以后慢慢细察。
当初为了寻觅一个简单的RGB直接转Lab算法而找遍网络皆不得,万不得已只好自力更生。其间虽费时一日,幸好也算略有所得。暂记于此,以利后人。其间或许难免错漏之处,还望达人不吝指点。
经转换后得到
///////////////////////////////////////////////////////////////////////////////////////////
//L = Y1 = (13933 * R + 46871 * G + 4732 * B) div 2^16
//a = 377 * (14503 * R - 22218 * G + 7714 * B) div 2^24 + 128
//b = 160 * (12773 * R + 39695 * G - 52468 * B) div 2^24 + 128
void RGB2Lab2(double R, double G, double B, double &L, double &a, double &b)
{
L = 0.2126007 * R + 0.7151947 * G + 0.0722046 * B;
a = 0.3258962 * R - 0.4992596 * G + 0.1733409 * B + 128;
b = 0.1218128 * R + 0.3785610 * G - 0.5003738 * B + 128;
}
//R = L1 + (a1 * 100922 + b1 * 17790) div 2^23
//G = L1 - (a1 * 30176 + b1 * 1481) div 2^23
//B = L1 + (a1 * 1740 - b1 * 37719) div 2^23
void Lab2RGB2(double L, double a, double b, double &R, double &G, double &B)
{
R = L + 0.0120308 * a + 0.0021207 * b;
G = L - 0.0035973 * a - 0.0001765 * b;
B = L + 0.0002074 * a - 0.0044965 * b;
}
///////////////////////////////////////////////////////////////////////////////////////////
转自:http://www.cnblogs.com/hrlnw/p/4126017.html
1.原理
RGB无法直接转换成LAB,需要先转换成XYZ再转换成LAB,即:RGB——XYZ——LAB
因此转换公式分两部分:
(1)RGB转XYZ
假设r,g,b为像素三个通道,取值范围均为[0,255],转换公式如下:
M=
0.4124,0.3576,0.1805
0.2126,0.7152,0.0722
0.0193,0.1192,0.9505
等同于如下公式:
X = var_R * 0.4124 + var_G * 0.3576 + var_B * 0.1805
Y = var_R * 0.2126 + var_G * 0.7152 + var_B * 0.0722
Z = var_R * 0.0193 + var_G * 0.1192 + var_B * 0.9505
上面的gamma函数,是用来对图象进行非线性色调编辑的,目的是提高图像对比度。这个函数不是唯一的,但是我在网上查到的基本都使用上式。
(2)XYZ转LAB
上面两个公式中,L*,a*,b*是最终的LAB色彩空间三个通道的值。X,Y,Z是RGB转XYZ后计算出来的值,Xn,Yn,Zn一般默认是95.047,100.0,108.883。
2.代码实现
(1)完全按照算法无优化实现(经@竹子小蜻蜓指正,原来代码有误,现已改正--206.04.12)
inline float gamma(float x) {return x>0.04045?pow((x+0.055f)/1.055f,2.4f):x/12.92;}; void RGBToLab(unsigned char*rgbImg,float*labImg) { float B=gamma(rgbImg[0]/255.0f); float G=gamma(rgbImg[1]/255.0f); float R=gamma(rgbImg[2]/255.0f); float X=0.412453*R+0.357580*G+0.180423*B; float Y=0.212671*R+0.715160*G+0.072169*B; float Z=0.019334*R+0.119193*G+0.950227*B;
float X/=0.95047;
float Y/=1.0;
float Z/=1.08883;
float FX = X > 0.008856f ? pow(X,1.0f/3.0f) : (7.787f * X +0.137931f); float FY = Y > 0.008856f ? pow(Y,1.0f/3.0f) : (7.787f * Y +0.137931f); float FZ = Z > 0.008856f ? pow(Z,1.0f/3.0f) : (7.787f * Z +0.137931f); labImg[0] = Y > 0.008856f ? (116.0f * FY - 16.0f) : (903.3f * Y); labImg[1] = 500.f * (FX - FY); labImg[2] = 200.f * (FY - FZ); }
上面是完全按照转换算法做的无优化的实现,里面涉及了大量的浮点运算,在PC上可能没什么问题,但是如果是在Android操作系统的移动端上,即使利用JNI,把转换算法写成C++版本进行加速,速度也不理想,因为这个操作时逐像素的,每个像素做几十次浮点运算,耗时还是十分巨大的。
(2)牺牲一些精度的快速实现
首先可以把gamma函数去掉,因为经过我的测试,这个函数带来的影响很小。
其次,M矩阵中的值都为小数,可以通过放大变成整数,接下来的计算就可以变成整数计算(在手机上浮点计算一般耗时是整形计算的几倍)。在这里,可以把M矩阵的值都扩大2^20倍变为整数,在计算得到X,Y,Z分量时再缩小回来。但是,XYZ的小数部分会消失,会引入误差,而在公式(5)(6)中(尤其是(6),涉及到指数运算和阈值运算,之前XYZ的误差在这里会被放大),这种误差还会继续传递给最终的L,a,b值。那怎么才能保证一定的准确率呢?
在这里我的方法是引入了一个查表机制。过程如下:
A.在计算XYZ的时候,参数扩大2^20倍,但最后缩小时只缩小2^18,这样计算出来的XYZ值范围是[0,1023]
B.建立一个table,用于将取值为[0,1023]的XYZ通过f(t)函数映射到中间结果,记为:LabTable(m)
C.将LabTable(m)代入公式(5)计算最终的Lab分量值
代码如下:
const static int big_shift=18; const static int HalfShiftValue=512; const static int shift=10; const static int offset=128<<shift; const static int ScaleLC = (16 * (1 << shift)); const static int ScaleLT = 116; const static int ScaleY= 903; const static int para1=500; const static int para2=200; const static int ThPara=9; void RGBToLab(unsigned char*rgbImg,int*labImg) { long long X=(rgbImg[0] * 199049 + rgbImg[1] * 394494 + rgbImg[2] * 455033 + 524288)>> (big_shift); long long Y=(rgbImg[0] * 75675 + rgbImg[1] * 749900 + rgbImg[2] * 223002 + 524288) >> (big_shift); long long Z=(rgbImg[0] * 915161 + rgbImg[1] * 114795 + rgbImg[2] * 18621 + 524288) >> (big_shift); labImg[0] = Y>ThPara?((ScaleLT * LabTable[Y] - ScaleLC + HalfShiftValue)>>shift):((ScaleY* Y)>>shift); labImg[1] = (para1*(LabTable[X] - LabTable[Y])+HalfShiftValue+offset)>>shift; labImg[2] = (para2*(LabTable[Y] - LabTable[Z])+HalfShiftValue+offset)>>shift; }
建立LabTable的代码如下:
int LabTable[1024]; for (int I = 0; I < 1024; I++) { if (I > 9) LabTable[I] = (int)(pow((float)I / 1020, 1.0F / 3) * (1 << 10) + 0.5 ); else LabTable[I] = (int)((29 * 29.0 * I / (6 * 6 * 3 * 1020) + 4.0 / 29) * (1 << 10) + 0.5 ); printf("%d,",LabTable[I]); }