逆矩阵介绍及C++/OpenCV/Eigen的三种实现

逆矩阵(inverse matrix)：在线性代数中，给定一个n阶方阵A，若存在一n阶方阵B，使得AB = BA =I_n，其中I_n为n阶单位矩阵，则称A是可逆的，且B是A的逆矩阵，记作A^-1.只有正方形(n*n)的矩阵，亦即方阵，才可能、但非必然有逆矩阵。若方阵A的逆矩阵存在，则称A为非奇异方阵或可逆方阵。与行列式类似，逆矩阵一般常用于求解包含数个变数的数学方程式。

线性方程组：Ax = b ,如下，其中A是一个已知矩阵，b是一个已知向量，x是我们要求解的未知向量。向量x的每一个元素x_i都是未知的。矩阵A的每一行和b中对应的元素构成一个约束。

线性代数提供了被称为矩阵逆(matrix inversion)的强大工具，对于大多数矩阵A，我们都能通过矩阵逆解析地求解式Ax=b。

单位矩阵(identity matrix)：任意向量和单位矩阵相乘，都不会改变。我们将保持n维向量不变的单位矩阵记作I_n，形式上如下，

单位矩阵的结构很简单：所有沿主对角线的元素都是1，而所有其他位置的元素都是0。

矩阵A的矩阵逆(matrix inversion)记作A^-1，其定义的矩阵满足如下条件：A^-1A = I_n，可以通过A^-1求解Ax = b，即x = A^-1b。当然，这取决于我们能否找到一个逆矩阵A^-1.

当逆矩阵A^-1存在时，有几种不同的算法都能找到它的闭解形式。理论上，相同的逆矩阵可用于多次求解不同向量b的方程。

逆矩阵性质：

(1)、若矩阵A是可逆的，则A的逆矩阵是唯一的。

(2)、可逆矩阵一定是方阵。

(3)、A的逆矩阵的逆矩阵还是A，记作(A^-1)^-1=A.

(4)、可逆矩阵A的转置矩阵A^T也可逆，并且(A^T)^-1=(A^-1)^T(转置的逆等于逆的转置)。

(5)、若矩阵A可逆，则矩阵A满足消去律，若AB=I(或BA=I)，则B=I，若AB=AC(或BA=CA)，则B=C。

(6)、两个可逆矩阵的乘积依然可逆。

(7)、矩阵可逆当且仅当它是满秩矩阵。

(8)、(λA)^-1=(1/λ)*A^-1

(9)、(AB)^-1=B^-1A^-1

(10)、det(A^-1)=1/det(A) (det为行列式)

(11)、方阵A可逆的充分必要条件是|A|≠0,并且A^-1=(1/|A|)A^*,其中A^*是A的伴随矩阵。即可逆矩阵就是非奇异矩阵(当|A|=0时，A称为奇异矩阵)。

如果逆矩阵A^-1存在，对于式Ax = b，肯定对于每一个向量b恰好存在一个解。

线性组合(linear combination)：形式上，一组向量的线性组合，是指每个向量乘以对应标量系数之后的和，即：

生成子空间(span)：一组向量的生成子空间是原始向量线性组合后所能抵达的点的集合。

确定Ax = b是否有解相当于确定向量b是否在A列向量的生成子空间中。这个特殊的生成子空间被称为A的列空间(column space)或者A的值域(range)。

线性无关(linearly independent)：如果一组向量中的任意一个向量都不能表示成其他向量的线性组合，那么这组向量被称为线性无关，反之称为线性相关(linearly  dependent)。如果某个向量是一组向量中某些向量的线性组合，那么我们将这个向量加入到这组向量后不会增加这组向量的生成子空间。这意味着，如果一个矩阵的列空间涵盖整个R^m,那么该矩阵必须包含至少一组m个线性无关的向量。这是式Ax = b对于每一个向量b的取值都有解的充分必要条件。值得注意的是，这个条件是说该向量集恰好有m个线性无关的列向量，而不是至少m个。不存在一个m维向量的集合具有多于m个彼此线性不相关的列向量，但是一个有多于m个列向量的矩阵却有可能拥有不止一个大小为m的线性无关向量集。

要想使矩阵可逆，我们还需要保证式Ax = b对于每一个b值至多有一个解。为此，我们需要确保该矩阵至多有m个列向量。否则，该方程会有不止一个解。

综上所述，这意味着该矩阵必须是一个方阵(square)，即m = n，并且所有列向量都是线性无关的。一个列向量线性相关的方阵被称为奇异的(singular)。

如果矩阵A不是一个方阵或者是一个奇异的方阵，该方程仍然可能有解。但是我们不能使用矩阵逆去求解。

对于方阵而言，矩阵的左逆和右逆是相等的：AA^-1=A^-1A=I

以上内容来自于 维基百科 和 《深度学习中文版》(https://github.com/exacity/deeplearningbook-chinese)

以下是分别用C++和OpenCV实现的矩阵求逆：

#include "funset.hpp"
#include 
#include 
#include 
#include 
#include 
#include "common.hpp"

#define EXP 1.0e-5

// 计算行列式
template
_Tp determinant(const std::vector>& mat, int N)
{
	if (mat.size() != N) {
		fprintf(stderr, "mat must be square matrix\n");
		return -1;
	}
	for (int i = 0; i < mat.size(); ++i) {
		if (mat[i].size() != N) {
			fprintf(stderr, "mat must be square matrix\n");
			return -1;
		}
	}

	_Tp ret{ 0 };

	if (N == 1) return mat[0][0];

	if (N == 2) {
		return (mat[0][0] * mat[1][1] - mat[0][1] * mat[1][0]);
	}
	else {
		// first col
		for (int i = 0; i < N; ++i) {
			std::vector> m(N - 1);
			std::vector m_rows;
			for (int t = 0; t < N; ++t) {
				if (i != t) m_rows.push_back(t);
			}
			for (int x = 0; x < N - 1; ++x) {
				m[x].resize(N - 1);
				for (int y = 0; y < N - 1; ++y) {
					m[x][y] = mat[m_rows[x]][y + 1];
				}
			}
			int sign = (int)pow(-1, 1 + i + 1);
			ret += mat[i][0] * sign * determinant<_Tp>(m, N - 1);
		}
	}

	return ret;
}

// 计算伴随矩阵
template
int adjoint(const std::vector>& mat, std::vector>& adj, int N)
{
	if (mat.size() != N) {
		fprintf(stderr, "mat must be square matrix\n");
		return -1;
	}
	for (int i = 0; i < mat.size(); ++i) {
		if (mat[i].size() != N) {
			fprintf(stderr, "mat must be square matrix\n");
			return -1;
		}
	}

	adj.resize(N);
	for (int i = 0; i < N; ++i) {
		adj[i].resize(N);
	}

	for (int y = 0; y < N; ++y) {
		std::vector m_cols;
		for (int i = 0; i < N; ++i) {
			if (i != y) m_cols.push_back(i);
		}

		for (int x = 0; x < N; ++x) {
			std::vector m_rows;
			for (int i = 0; i < N; ++i) {
				if (i != x) m_rows.push_back(i);
			}

			std::vector> m(N - 1);
			for (int i = 0; i < N - 1; ++i) {
				m[i].resize(N - 1);
			}
			for (int j = 0; j < N - 1; ++j) {
				for (int i = 0; i < N - 1; ++i) {
					m[j][i] = mat[m_rows[j]][m_cols[i]];
				}
			}

			int sign = (int)pow(-1, x + y);
			adj[y][x] = sign * determinant<_Tp>(m, N-1);
		}
	}

	return 0;
}

template
void print_matrix(const std::vector>& mat)
{
	int rows = mat.size();
	for (int y = 0; y < rows; ++y) {
		for (int x = 0; x < mat[y].size(); ++x) {
			fprintf(stderr, "  %f  ", mat[y][x]);
		}
		fprintf(stderr, "\n");
	}
	fprintf(stderr, "\n");
}

void print_matrix(const cv::Mat& mat)
{
	assert(mat.channels() == 1);

	for (int y = 0; y < mat.rows; ++y) {
		for (int x = 0; x < mat.cols; ++x) {
			if (mat.depth() == CV_8U) {
				unsigned char value = mat.at(y, x);
				fprintf(stderr, "  %d  ", value);
			}
			else if (mat.depth() == CV_32F) {
				float value = mat.at(y, x);
				fprintf(stderr, "  %f  ", value);
			}
			else if (mat.depth() == CV_64F) {
				double value = mat.at(y, x);
				fprintf(stderr, "  %f  ", value);
			}
			else {
				fprintf(stderr, "don't support type: %d\n", mat.depth());
				return;
			}
		}
		fprintf(stderr, "\n");
	}
	fprintf(stderr, "\n");
}

// 求逆矩阵
template
int inverse(const std::vector>& mat, std::vector>& inv, int N)
{
	if (mat.size() != N) {
		fprintf(stderr, "mat must be square matrix\n");
		return -1;
	}
	for (int i = 0; i < mat.size(); ++i) {
		if (mat[i].size() != N) {
			fprintf(stderr, "mat must be square matrix\n");
			return -1;
		}
	}

	_Tp det = determinant(mat, N);
	if (fabs(det) < EXP) {
		fprintf(stderr, "mat's determinant don't equal 0\n");
		return -1;
	}

	inv.resize(N);
	for (int i = 0; i < N; ++i) {
		inv[i].resize(N);
	}

	double coef = 1.f / det;
	std::vector> adj;
	if (adjoint(mat, adj, N) != 0) return -1;

	for (int y = 0; y < N; ++y) {
		for (int x = 0; x < N; ++x) {
			inv[y][x] = (_Tp)(coef * adj[y][x]);
		}
	}

	return 0;
}

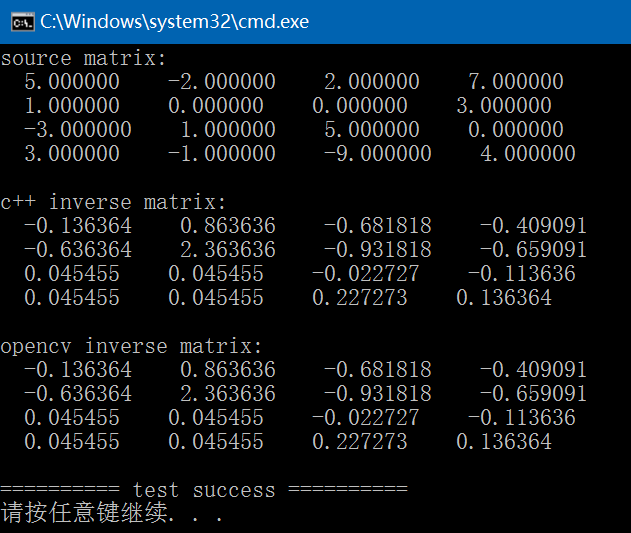
int test_inverse_matrix()
{
	std::vector vec{ 5, -2, 2, 7, 1, 0, 0, 3, -3, 1, 5, 0, 3, -1, -9, 4 };
	const int N{ 4 };
	if (vec.size() != (int)pow(N, 2)) {
		fprintf(stderr, "vec must be N^2\n");
		return -1;
	}

	std::vector> arr(N);
	for (int i = 0; i < N; ++i) {
		arr[i].resize(N);

		for (int j = 0; j < N; ++j) {
			arr[i][j] = vec[i * N + j];
		}
	}

	std::vector> inv1;
	int ret = inverse(arr, inv1, N);

	fprintf(stderr, "source matrix: \n");
	print_matrix(arr);
	fprintf(stderr, "c++ inverse matrix: \n");
	print_matrix(inv1);

	cv::Mat mat(N, N, CV_32FC1, vec.data());
	cv::Mat inv2 = mat.inv();
	fprintf(stderr, "opencv inverse matrix: \n");
	print_matrix(inv2);

	return 0;
}

执行结果如下：

以下是用Eigen实现的矩阵求逆：

#include "funset.hpp"
#include 
#include 
#include 
#include 
#include 
#include 
#include "common.hpp"

template
void print_matrix(const _Tp* data, const int rows, const int cols)
{
	for (int y = 0; y < rows; ++y) {
		for (int x = 0; x < cols; ++x) {
			fprintf(stderr, "  %f  ", static_cast(data[y * cols + x]));
		}
		fprintf(stderr, "\n");
	}
	fprintf(stderr, "\n");
}

int test_inverse_matrix()
{
	std::vector vec{ 5, -2, 2, 7, 1, 0, 0, 3, -3, 1, 5, 0, 3, -1, -9, 4 };
	const int N{ 4 };
	if (vec.size() != (int)pow(N, 2)) {
		fprintf(stderr, "vec must be N^2\n");
		return -1;
	}

	Eigen::Map map(vec.data(), 4, 4);
	Eigen::MatrixXf inv = map.inverse();

	fprintf(stderr, "source matrix:\n");
	print_matrix(vec.data(), N, N);
	fprintf(stderr, "eigen inverse matrix:\n");
	print_matrix(inv.data(), N, N);

	return 0;
}

执行结果如下：

可见，三种实现方法结果是一致的。

GitHub：

https://github.com/fengbingchun/NN_Test

https://github.com/fengbingchun/Eigen_Test