unity 旋转欧拉角 万向锁 解释
万向锁 一直困惑我很久。。。。原因出在这里,我以为欧拉角旋转是以模型坐标(齐次坐标系)为旋转轴。问题就来了,无论旋转那个轴,其它两个轴也会相应的变化,下面看图:
根据上面的说明两个旋转面(圆圈)怎么会共面,让我迷糊。假设共面,那这两个旋转面的法线应该是旋转轴,要想两个面共面,那旋转轴肯定平行的。但问题是以模型坐标(齐次坐标系)为旋转轴,无论旋转那个轴,其它两个轴也会相应的变化,而且相互垂直。就不会发生共面,不会出现万象锁???
网上说欧拉角坐标轴旋转是按顺序旋转的,即父子关系,如下图
还是不明白上图的旋转轴在哪???!
下面我用unity演示一下
从上面看,无论旋转那个轴,旋转后,他们的旋转轴都是垂直的。假设绕x轴旋转,y轴和z轴所确立的面就是这个变换的旋转面。问题来了,既然无论怎么旋转,旋转轴都是垂直的,当你旋转是其他轴所确立的旋转面也会旋转,保持垂直关系。那怎么会出现两个旋转面共面呢??
下面开始说明万象锁(以unity 3D 说明)
先说明unity 3D欧拉角的旋转顺序(父子关系)是y-x-z。即旋转y轴x和z轴都变,旋转x轴只有z轴变化,旋转z轴其它轴不变。
再解释说明前,先说明一些坐标概念。
模型坐标系---及模型导入时的坐标系,通过此坐标系记录模型顶点等的位置。
世界坐标系---主要作用是表示模型与模型间的相对位置。
惯性坐标系---和模型坐标系原点相同,但是坐标轴的方向和世界坐标系相同,作用应该是模型到世界变换的桥梁吧。
具体请参照图书《3D数学基础:图形与游戏开发》
引入惯性坐标是为了便于说明(实事上旋转是在一个坐标系上进行的)(在总结的时候会加以说明)
unity模型坐标系和惯性坐标系间的查看方法
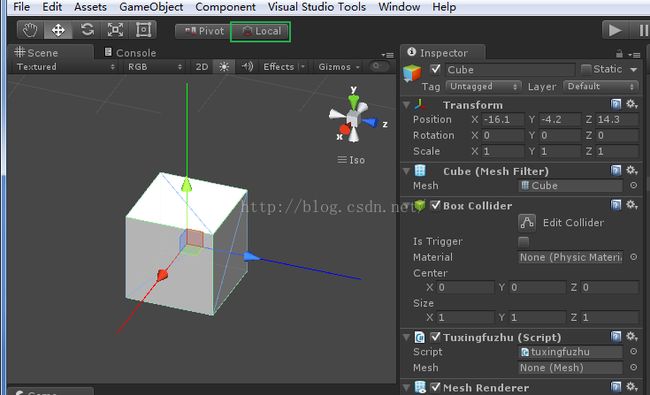
local为模型坐标系
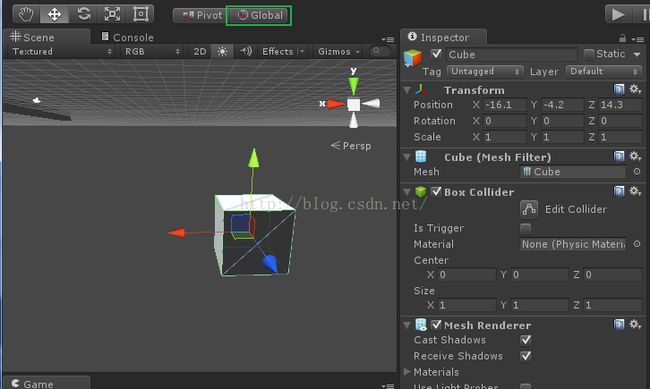
global为惯性坐标系
如果你不旋转模型,此时惯性坐标系和模型坐标系重合,你可以点选上面按钮切换看一下。
ok,为了方便说明,我们用辅助线将惯性坐标系画到模型上,坐标轴颜色和模型坐标轴相对应
代码如下:
先创建一个脚本,名称为tuxingfuzhu.cs脚本,
代码:
using UnityEngine;
using System.Collections;
//using UnityEditor;
public class tuxingfuzhu : MonoBehaviour {
public Mesh mesh;
// Use this for initialization
void Start () {
}
///
/// 如果你想绘制可被点选的gizmos,执行这个函数
///
void OnDrawGizmos()
{
Gizmos.color = Color.red;
Vector3 direction = Vector3.right* 2; //世界坐标系的 轴向x
Gizmos.DrawRay(transform.position, direction);
Gizmos.color = Color.green;
direction = Vector3.up* 2; //世界坐标系的 轴向y
Gizmos.DrawRay(transform.position, direction);
Gizmos.color = Color.blue;
direction = Vector3.forward* 2; //世界坐标系的 轴向z
Gizmos.DrawRay(transform.position, direction);
}
///
/// 如果你想在物体被选中时绘制gizmos,执行这个函数
///
void OnDrawGizmosSelected()
{
//Gizmos.color = Color.white;
//Gizmos.DrawSphere(transform.position, 1);
}
// Update is called once per frame
void Update () {
}
}
代码说明
Gizmos.DrawRay //绘制辅助射线,有关辅助工具请查阅unity官网的Gizmos类。
然后将脚本挂载到要测试的物体上,这里我挂在到了cube物体上,效果如下:
我们看到模型多了三条长线(惯性坐标)。
ok,现在进行旋转说明。
首先将坐标切换到模型坐标,
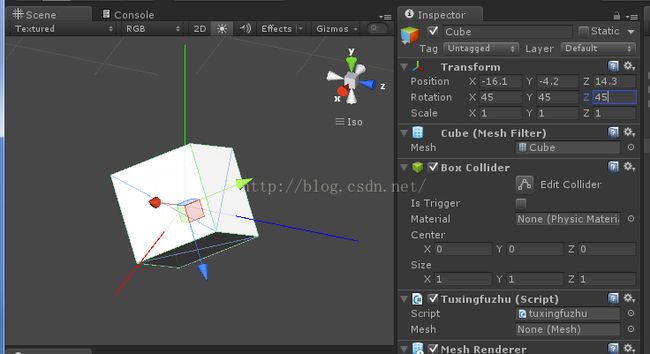
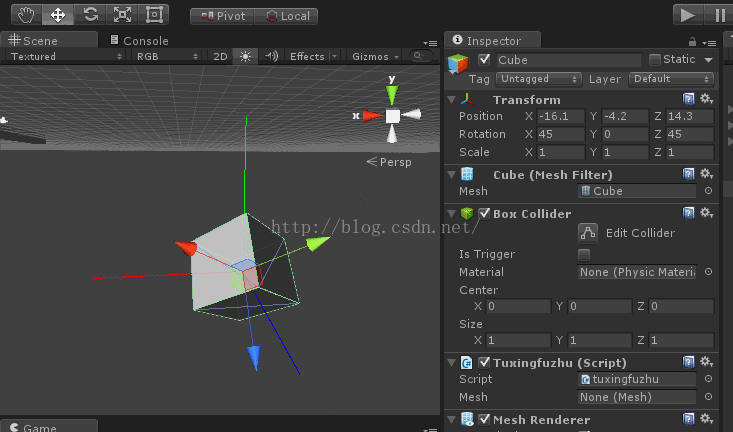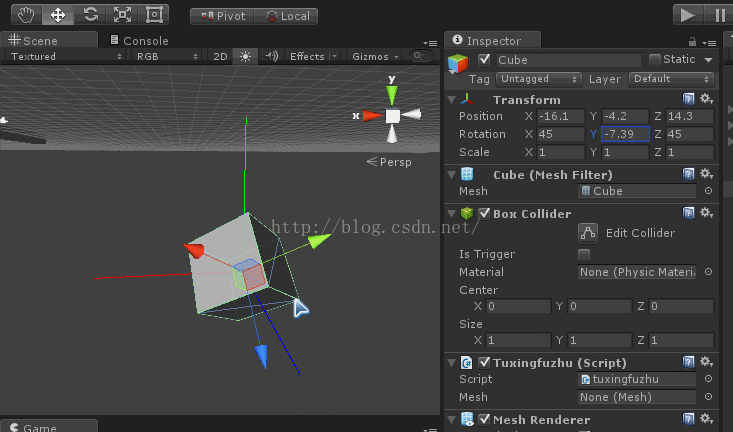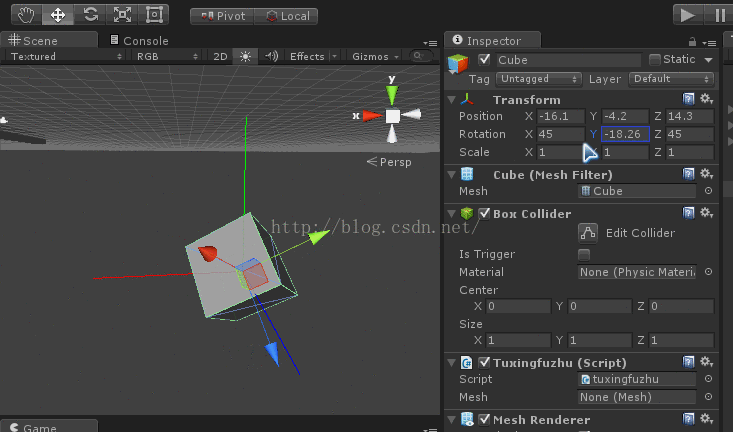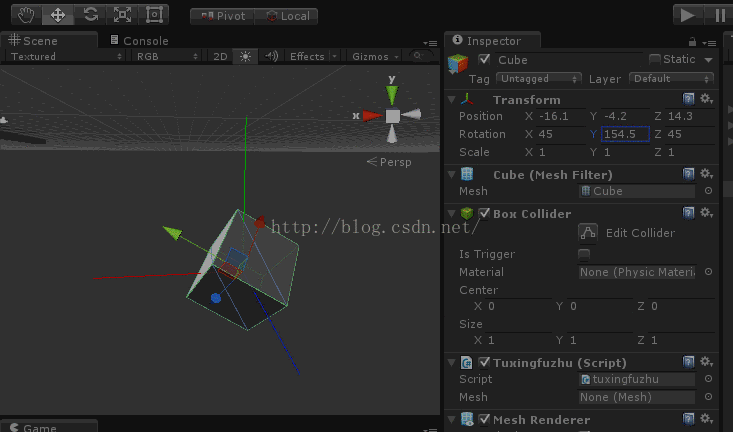
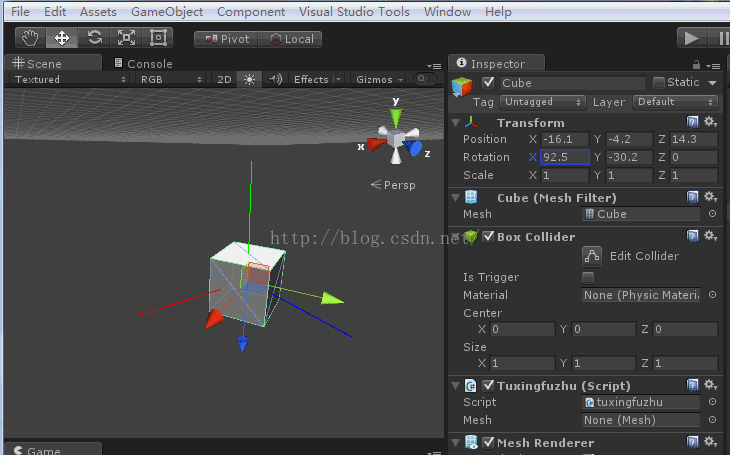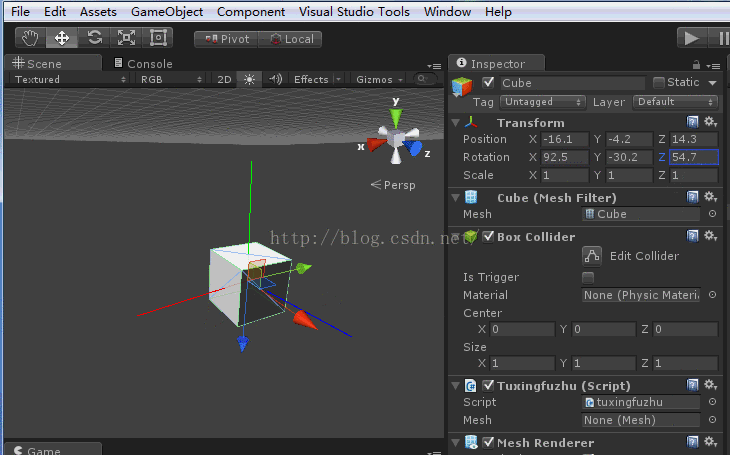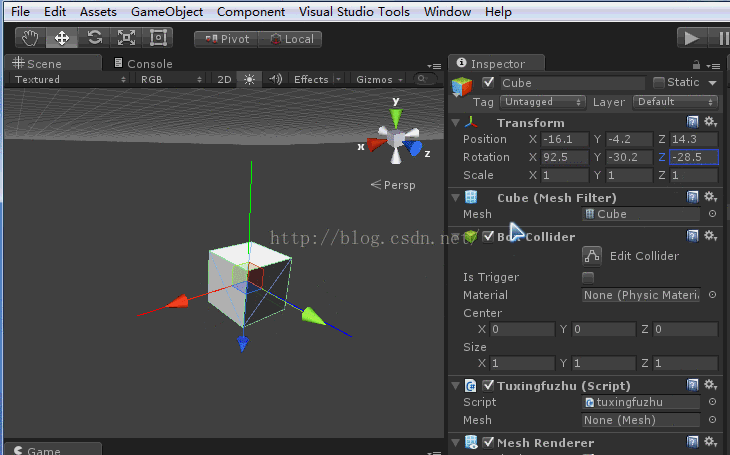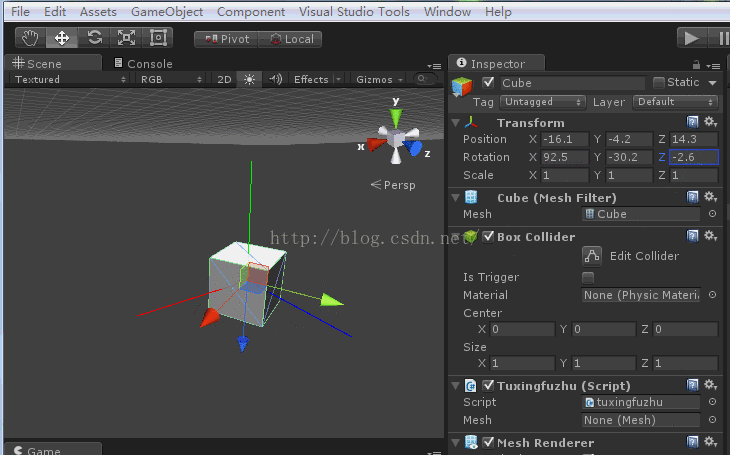
下面将模型x和z轴分别旋转45度。
点选你的测试模型,效果如下图
ok,现在模型坐标和惯性坐标分离了。
好,现在我们开始旋转最顶层的y轴。
效果如下图:
你发现了什么???
你会发现旋转y轴是绕着惯性左边的y轴旋转的,而不是模型的坐标。
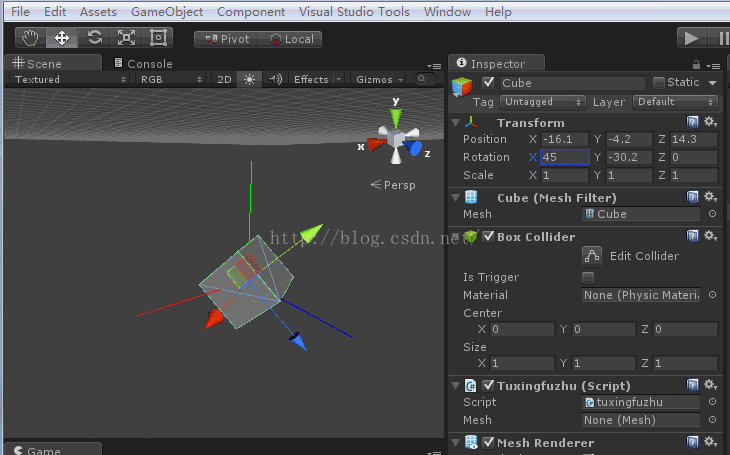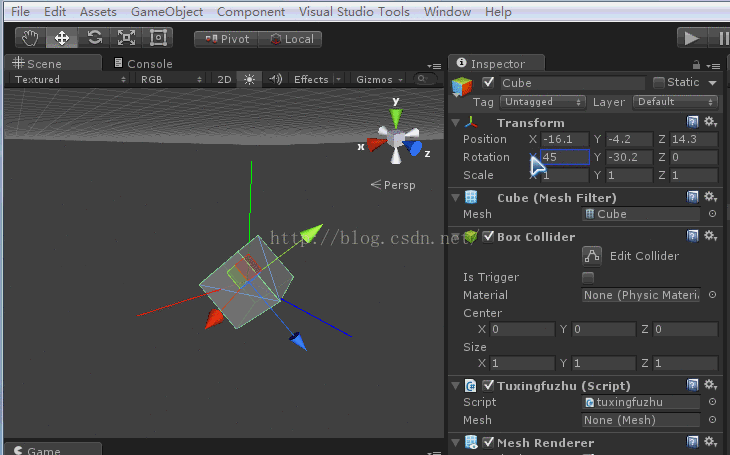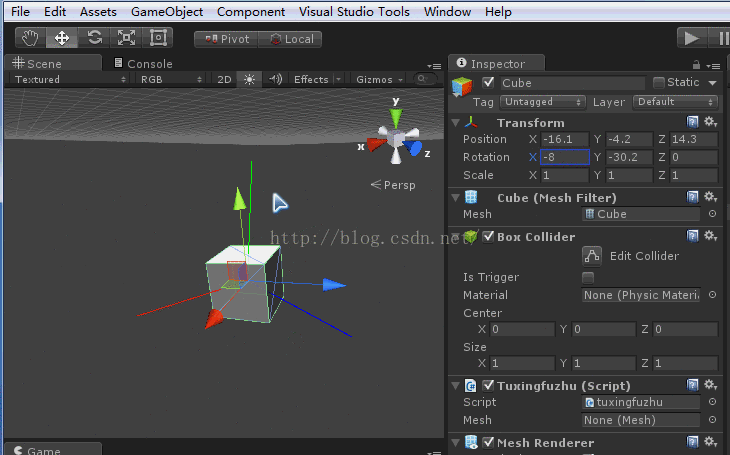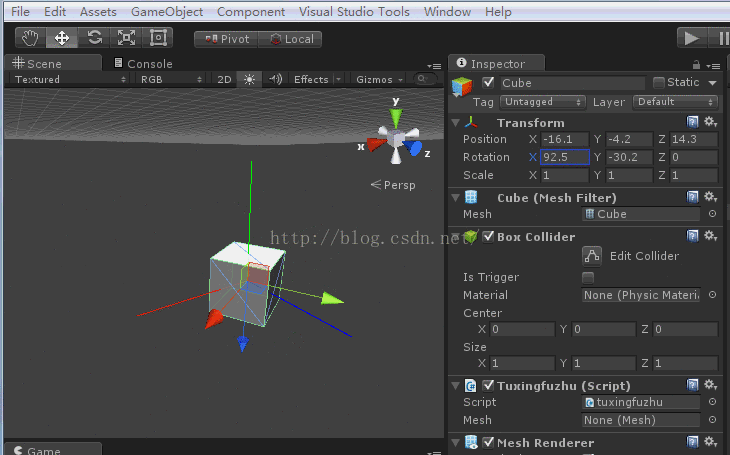
ok,现在将z轴置0,然后旋转x轴,y轴可以有一定的度数,为了作对照。
效果如下图:
此时你会发现x轴的变换是绕着模型坐标的x轴进行变换的。
ok,接着进行z轴的变换,如下图:
你会发现z轴的变换也是绕着模型的z轴变换。
到这里问题就差不多了。为什么会共面,因为y轴变换将影响x和z轴,因为有轴处在变换的最顶层(y-x-z),最主要的是y轴变换是模型在惯性坐标里变换,而其他轴的变换是在模型轴变换。所以就会出旋转面共面(万向锁)的情况
下面开始说明万向锁的情况。
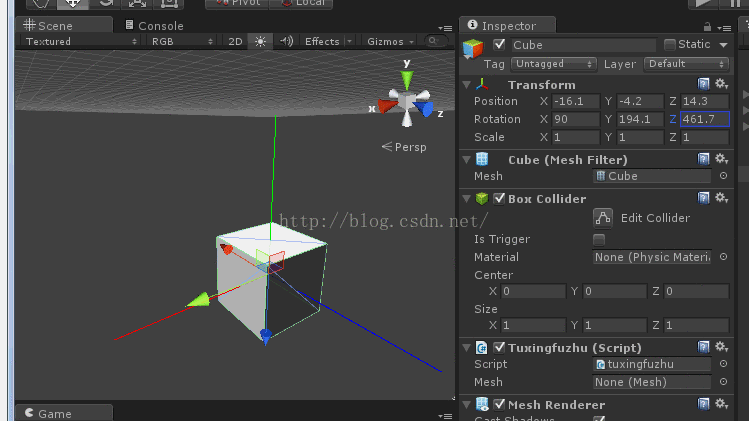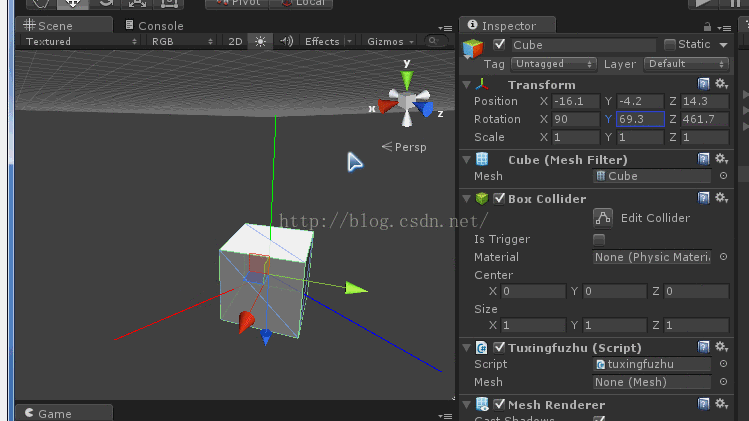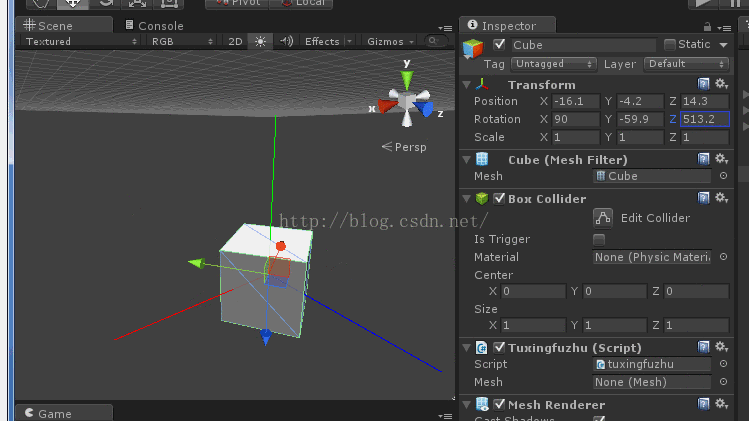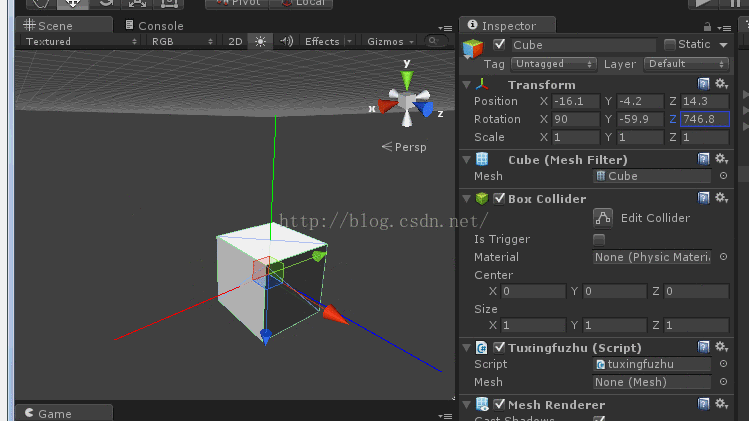
将模型x轴旋转90度(或者-90度)(最简单的万向锁)
紧接着旋转y轴或者z轴,效果如下:
这就是万向锁
你会发现z轴旋转和y轴旋转效果是一样的,同时你会发现z轴(模型坐标系)和y轴坐标(惯性坐标系)平行。
此时y轴(惯性坐标系)旋转面和z轴(模型坐标系)旋转面共面如下图,
从上图很容易看出旋转y轴(惯性坐标系)和旋转z轴(模型坐标系)是一样的效果,只不过方向相反或相同。
让我困惑的问题解决了。
总结:
万向锁产生时两个旋转轴平行(旋转面共面)是模型的旋转失去的一个方向的旋转。
最主要的是弄明白旋转是围绕着什么样的坐标系做旋转。
上面的解释只是从表面上解释了万向锁
实际上模型的旋转是以一个坐标系进行旋转。但上面解释是等效的。下面解释一下。
计算机模型的旋转过程不是我们想的连续旋转。什么意思呢?
假设U3D每一帧绕Y旋转5度,他的旋转过程是:第一次旋转从(0,0,0)绕Y轴旋转5度为(0,5,0),到现在还没有问题,那第二次旋转会是什么情况呢。
有人说,简单,再从现在以变换的模型旋转(0,5,0)绕Y轴旋转5度---->(0,10,0)不就行了。但计算机不会这样做。它是在原模型坐标(0,0,0)重新开始变化,
即(0,0,0)------>(0,10,0)。
就是说模型的变换都是(0,0,0)开始变换,主意,知道这一点才是最主要的。
当模型绕Y-X-Z顺序旋转时,当模型发生旋转变换时:
步骤1.每次变换的顺序都是(0,0,0)-------------->(x,y,z),即都是从(0,0,0)开始,先变换Y轴,在变换X轴,然后在变换轴。
每次只要有变换,都要重复步骤1的过程。
每次旋转都先绕Y轴旋转,所以每次旋转变换的Y轴方向是不变的,和惯性坐标重合。所以我上面的旋转是以惯性坐标去解释。其实这个困惑是时间上的先后顺序产生的,准确的
说是时间上的共轴或共面
下面我演示变换过程如下图:
上面演示了三次图形变换(0,0,0)----->(58,67,40); (0,0,0)-------->(45,87,60); (0,0,0)-------->(45,67,67)
在变换时,内部程序都是从(0,0,0)开始变换(算法)的。即使你再U3D参数设置上可以在现有的变换进行变换,但程序内部还是从(0,0,0)开始变换。
从上面三次(或者更多次)变换,你会发现三次变换的第一次Y轴变换的轴是一样的。绿色的圆为旋转面。
接下来是X轴旋转,z轴旋转。即使Y轴变换了,但是三次变化在第一次绕y轴变换的时刻Y轴是不变的。所以y轴与Z轴会有共线,或者说Y轴的旋转轴和Z轴的旋转轴共面只
是在时间变换上的共面。(万向锁的产生)
在U3D中,旋转顺序是y-x-z(模型坐标---惯性坐标系旋转),官网为z-x-y(惯性坐标系----模型坐标)。
y轴是惯性坐标系的y轴,其它轴是模型的坐标轴。这是因为不同坐标系的轴才有可能产生共面
如果不明白坐标系的,具体请查阅《3D数学基础:图形与游戏开发》图书。
打个广告吧。推荐一下吧,非常基础,非常形象易懂的图形学图书。
万象锁有关视频
http://v.youku.com/v_show/id_XNzkyOTIyMTI=.html