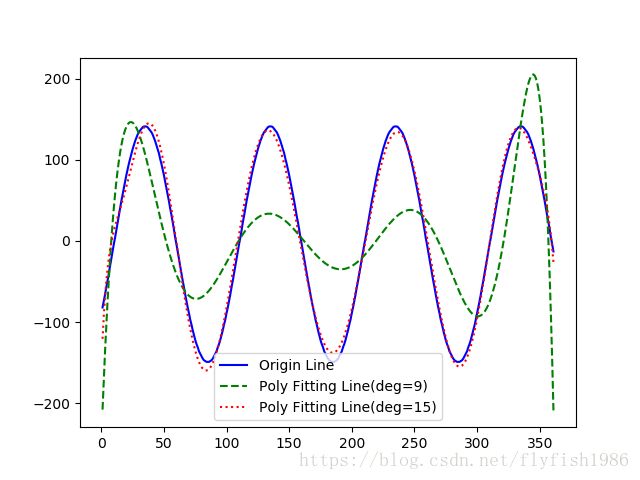
周期函数的拟合
周期函数的拟合
flyfish
类似sin函数的拟合
import numpy as np
import matplotlib.pyplot as plt
x= np.arange(1, 362, 1)
y = np.array([-82,-74,-66,-57,-49,-40,-31,-22,-13,-4,4,13,22,31,40,49,57,65,73,81,88,95,101,107,113,118,123,127,131,134,136,138,140,141,141,141,140,138,
136,134,131,127,123,118,113,108,101,95,88,81,73,65,57,49,40,32,23,14,4,-4,-13,-22,-31,-40,-49,-57,-66,-74,-82,-89,-97,-103,-110,-116,-122,
-127,-131,-136,-139,-142,-145,-147,-148,-149,-149,-149,-148,-147,-145,-142,-139,-136,-131,-127,-122,-116,-110,-103,-97,-89,-82,-74,-66,-57,
-49,-40,-31,-22,-13,-4,4,13,23,31,40,49,57,65,73,81,88,95,101,107,113,118,123,127,131,134,136,138,140,141,141,141,140,138,136,134,131,127,
123,118,113,108,101,95,88,81,73,65,57,49,40,31,23,14,4,-4,-13,-22,-31,-40,-49,-57,-66,-74,-82,-89,-97,-103,-110,-116,-122,-127,-131,-136,-139,
-142,-145,-147,-148,-149,-149,-149,-148,-147,-145,-142,-139,-136,-131,-127,-122,-116,-110,-103,-97,-89,-82,-74,-66,-57,-49,-40,-31,-22,-13,-4,
4,13,22,31,40,49,57,65,73,81,88,95,101,107,113,118,123,127,131,134,136,138,140,141,141,141,140,138,136,134,131,127,123,118,113,107,101,95,88,81,
73,65,57,49,40,31,23,14,4,-4,-13,-22,-31,-40,-49,-57,-66,-74,-82,-89,-97,-103,-110,-116,-122,-127,-131,-136,-139,-142,-145,-147,-148,-149,-149,
-149,-148,-147,-145,-142,-139,-136,-131,-127,-122,-116,-110,-104,-97,-89,-82,-74,-66,-57,-49,-40,-31,-22,-13,-4,4,13,22,31,40,49,57,65,73,81,88,
95,101,107,113,118,123,127,131,134,136,138,140,141,141,141,140,138,136,134,131,127,123,118,113,107,101,95,88,81,73,65,57,49,40,31,23,14,4,-4,-13])
print(x.shape)
print(y.shape)
# 对比拟合的参数
fitting1 = np.polyfit(x, y, 9)
fitting2 = np.polyfit(x, y, 12)
# 生成多项式对象
polynomial1 = np.poly1d(fitting1)
polynomial2 = np.poly1d(fitting2)
print(polynomial2)
# 绘制曲线 # 原曲线
plt.plot(x, y, 'b-', label='Origin Line')
plt.plot(x, polynomial1(x), 'g--', label='Poly Fitting Line(deg=9)')
plt.plot(x, polynomial2(x), 'r:', label='Poly Fitting Line(deg=15)')
plt.legend()
plt.savefig('fitting.png')
plt.show();
fmt = '[color][marker][line]'
character color
‘b’ blue
‘g’ green
‘r’ red
‘c’ cyan
‘m’ magenta
‘y’ yellow
‘k’ black
‘w’ white
character description
‘.’ point marker
‘,’ pixel marker
‘o’ circle marker
‘v’ triangle_down marker
‘^’ triangle_up marker
‘<’ triangle_left marker
‘>’ triangle_right marker
‘1’ tri_down marker
‘2’ tri_up marker
‘3’ tri_left marker
‘4’ tri_right marker
‘s’ square marker
‘p’ pentagon marker
‘*’ star marker
‘h’ hexagon1 marker
‘H’ hexagon2 marker
‘+’ plus marker
‘x’ x marker
‘D’ diamond marker
‘d’ thin_diamond marker
‘|’ vline marker
‘_’ hline marker
Line Styles
character description
‘-’ solid line style
‘–’ dashed line style
‘-.’ dash-dot line style
‘:’ dotted line style
例子
‘b’ # blue markers with default shape
‘ro’ # red circles
‘g-’ # green solid line
‘–’ # dashed line with default color
‘k^:’ # black triangle_up markers connected by a dotted line
方法2
使用线性回归算法拟合正弦函数
代码摘自《scikit-learn机器学习》
import matplotlib.pyplot as plt
import numpy as np
n_dots = 200
X = np.linspace(-2 * np.pi, 2 * np.pi, n_dots)
Y = np.sin(X) + 0.2 * np.random.rand(n_dots) - 0.1
X = X.reshape(-1, 1)
Y = Y.reshape(-1, 1)
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
def polynomial_model(degree=1):
polynomial_features = PolynomialFeatures(degree=degree,
include_bias=False)
linear_regression = LinearRegression(normalize=True)
pipeline = Pipeline([("polynomial_features", polynomial_features),
("linear_regression", linear_regression)])
return pipeline
from sklearn.metrics import mean_squared_error
degrees = [2, 3, 5, 10]
results = []
for d in degrees:
model = polynomial_model(degree=d)
model.fit(X, Y)
train_score = model.score(X, Y)
mse = mean_squared_error(Y, model.predict(X))
results.append({"model": model, "degree": d, "score": train_score, "mse": mse})
for r in results:
print("degree: {}; train score: {}; mean squared error: {}".format(r["degree"], r["score"], r["mse"]))
from matplotlib.figure import SubplotParams
plt.figure(figsize=(12, 6), dpi=200, subplotpars=SubplotParams(hspace=0.3))
for i, r in enumerate(results):
fig = plt.subplot(2, 2, i + 1)
plt.xlim(-8, 8)
plt.title("LinearRegression degree={}".format(r["degree"]))
plt.scatter(X, Y, s=5, c='b', alpha=0.5)
plt.plot(X, r["model"].predict(X), 'r-')
plt.show()
拟合方法2
import matplotlib.pyplot as plt
import pandas as pd
import math
import numpy as np
from scipy import optimize
from scipy.optimize import fsolve
from scipy.optimize import leastsq
# y=Asin(ωx+φ)
# y=Asin(2*PI/B+C)
#数据
x= np.arange(1, 140, 1)
y = np.array([55,65,74,82,90,97,103,109,114,118,120,122,123,124,123,121,118,114,
110,104,98,91,83,75,66,57,47,36,26,15,4,-6,-17,-27,-38,-48,-58,-67,
-76,-84,-92,-99,-105,-111,-115,-119,-121,-123,-124,-124,-122,-120,
-117,-113,-109,-103,-96,-89,-81,-73,-64,-54,-44,-34,-23,-12,-2,8,19,
30,40,51,60,70,78,86,94,101,107,112,116,119,122,123,124,123,122,119,
116,112,107,101,94,87,79,70,61,51,41,31,20,9,-1,-12,-23,-33,-44,-54,
-63,-72,-81,-89,-96,-103,-108,-113,-117,-120,-122,-123,-124,-123,-121,
-119,-115,-111,-105,-99,-92,-85,-76,-68,-58,-48,-38,-28,-17,-6,4])
def func(x, P):
#数据拟合所用的函数: Asin(2*PI/B+C)
A,B,C = P
return A * np.sin(x * 2 * np.pi / B + C)
def cost( P, y, x):
# 实验数据x, y和拟合函数之间的差
return (abs((y**2) - (func(x,P) **2)))**0.5
p0 = [100, 70,0.1]
# p0为拟合参数的初始值
result = leastsq(cost, p0, args=(y, x))
print(result)
print ("actual parameter:", p0) # 真实参数
print ("fitting parameter", result[0]) # 实验数据拟合后的参数
plt.plot(x, y, label="original data") # 绘制真实数据
plt.plot(x, func(x, result[0]), label="fitting data") # 拟合数据
plt.legend()
plt.show()
# actual parameter: [100, 70, 0.1]
# fitting parameter [123.53408412 71.43291803 0.37639757]