prophet模型小结

1. Introduction
在许多自然科学或商业活动中，对于时间序列的预测起着非常重要的作用。但是，做出高精度的预测无论对计算机还是对人类分析师来说都不是一个简单的事情。主要有两个原因：1.完全自动化的预测模型灵活性很差，很难考虑到一些有用的假设或一些具有启发性的条件。2.分析师一般对本领域有深刻的理解，但是对于时间序列的预测往往经验不足。

本研究要做的是为不同情况下的预测行为提供一些有用的指导，主要有以下几种情况：
1.众多进行时间序列预测，却没有受过训练的人；
2.众多预测的任务，这些任务存在潜在的异常点；
3.在数量众多的预测任务开展时，让机器进行苛刻的对比和评价，而让分析师进行反馈并提升模型的表现。

2. Features of Business Time Series

图1 Facebook上发生的事件数目
图1所示的是Facebook上的事件随时间变化的情况，每种颜色表示一周内的某天发生的事件数目，这些事件包括创建新网页，邀请其他人等。从图中可以看到几个明显的特点：
1. 周期性特点，一周和一年的周期性；
2. 节假日的影响，在新年和圣诞节发生了显著的下降；
3. 趋势，最后六个月有明显的上升，这是由于新产品发布或市场发生了变动；
4. 异常值，真实数据集中经常出现异常值。

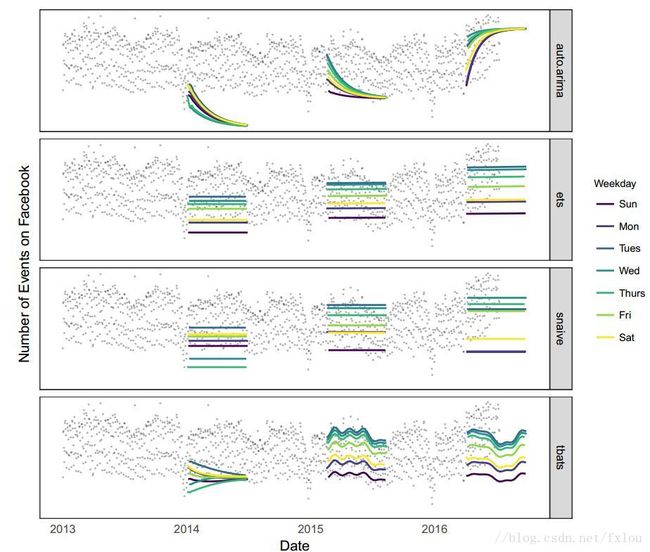
图2 几种自动预测模型的预测结果
图2所示的是采用几个不同的自动预测模型的预测结果，从图1中的数据中选取了3个不同的点进行预测。具体如下：
1. auto.arima，拟合出一系列ARIMA模型，并自动选出最好的一个；
2. ets,拟合出一些列指数平滑模型，并选出最好的一个；
3. snaive，随机行走模型，随着一周的周期性做出固定的预测；
4. tbats，考虑一周和一年的周期性。
以上模型的不足：
当在预测点前存在趋势变化时，auto.arima模型预测出的趋势误差较大，且不能考虑周期性特点。ets和snaive考虑了一周的周期性，但是不能考虑长期的周期性特点。所有这些模型在每一年的年末的预测都产生了过激的反应，因为他们不能够考虑一年的周期性，如图3中2014年的位置，所有模型预测结果都偏低。

3. The Prophet Forecasting Model
prophet模型的构成如下：

y(t)=g(t)+s(t)+h(t)+ϵ y ( t ) = g ( t ) + s ( t ) + h ( t ) + ϵ

其中， g(t) g ( t ) 是趋势(trend)函数，用来分析时间序列中非周期性的变化。 s(t) s ( t ) 代表周期性的变化，例如一周或一年的周期性。 h(t) h ( t ) 代表节假日等偶然一天或几天造成的影响。 ϵ ϵ 是误差项，代表本模型没有考虑到的误差的影响。

这种设置与GAM（Hastile,1987）方法类似，GAM方差对回归量进行了各种非线性平滑后，加入到了回归模型中。本文的模型只采用时间作为回归量，有时候也将几个时间的线性或非线性函数加入进来。

GAM方法的优势是它能够很容易地进行分解，并适应新的成分，例如当新的周期性确定时。同时，GAM不论采用backfitting还是L-BFGS（本文采用后者）都能够快速拟合，这将有利于用户能够交互地进行模型参数调整。

本文模型的主要优点如下：
1. 灵活性：能够很容易地调整周期性，并且让用户对趋势进行不同的假设。
2. 与ARIMA模型不同，这些测量值不需要具有规则地间隔，也不需要对缺失值进行插值。
3. 拟合速度快
4. 预测模型具有容易解释的参数，能够让分析者针对不同的假设进行改进。

3.1 The Trend Model
3.1.1 Nonlinear, Saturating Growth
Facebook中模型的增长类似于生态系统中种族数量的增长，在经历非线性增长后到达饱和值，这种类型的增长常采用logistic增长模型，基本形式如下：

g(t)=C1+exp(−k(t−m)) g ( t ) = C 1 + e x p ( − k ( t − m ) )

其中，C是饱和值（承载能力），k是增长率，m是偏置参数。
对于facebook，该模型需要改进，首先是饱和值C是随时间变化的，其次增长率也会随着新产品发布等原因发生变化。
在时间序列中设置若干个转变点 sj,j=1,...,S s j , j = 1 , . . . , S ，在这些转变点增长率会发生变化，变化量用 δj δ j 表示在时间 tj t j 处的变化量，构建出向量 a(t)∈{0,1}S a ( t ) ∈ { 0 , 1 } S

aj(t)={1,t≥sj,0,otherwise a j ( t ) = { 1 , t ≥ s j , 0 , o t h e r w i s e

则增长率在时间 t t 的表达式变为：

k+a(tT)δ k + a ( t T ) δ

当增长率发生变化时，偏置参数 m m 也应该做出相应的调整，来连接时间片段的尾部。在转折点 j j 处对偏置的调整量如下：

γj=(sj−m−∑l<jγl)(1−k+∑l<jδlk+∑l≤jδl) γ j = ( s j − m − ∑ l < j γ l ) ( 1 − k + ∑ l < j δ l k + ∑ l ≤ j δ l )

那么就得到分段logistic趋势模型：

g(t)=C(t)1+exp(−(k+a(t)T)δ)(t−(m+a(t)T)γ) g ( t ) = C ( t ) 1 + e x p ( − ( k + a ( t ) T ) δ ) ( t − ( m + a ( t ) T ) γ )

3.1.2 Linear Trend with Changepoints
当要预测的问题没有饱和增长的趋势时，分段连续增长率模型有时候非常有效，表达式如下：

g(t)=(k+a(t)Tδ)t+(m+a(t)Tγ) g ( t ) = ( k + a ( t ) T δ ) t + ( m + a ( t ) T γ )

与前面类似，k是增长率， δ δ 是增长率的调整值，m是偏置参数， γj γ j 设置为 −sjδj − s j δ j 来使得函数连续。

3.1.3 Automatic Changepoint Selection
转变点 sj s j 的选择可以根据产品发布时间或其他影响增长率变化事件时间来指定，或者给定一个待选值的集合并自动确定。自动确定转变点可以通过将3.1.1和3.1.2中的方程中的 δ δ 设置一个稀疏先验来实现。

通常设置大量的转折点（例如，连续几年的时间内每个月设置一个转折点），并采用先验 δ δ ~ Laplace(0,τ) L a p l a c e ( 0 , τ ) 。其中， τ τ 直接控制增长率改变的灵活性， δ δ 稀疏先验对主要增长率k没有影响，当 τ τ 变为0时，模型变为标准的Logistic或线性模型。

3.1.4 Trend Forecast Uncertainty
当基于历史数据对模型外推进行预测时，趋势将会有一个固定值。为了估计趋势的不确定性，将生成模型向前扩展。针对趋势的生成模型是这样的，在T个历史数据中的分布着S个转折点，每个转折点的增长率改变量为 δ δ ~ Laplace(0,τ) L a p l a c e ( 0 , τ ) 。

对未来增长率的变化的预测按照以前的方式来，不过要将 τ τ 替换为一个从数据中推断出的方差。在贝叶斯架构中，可以通过对 τ τ 设置多层先验分布来得到它的后验分布，或者可以使用增长率尺度参数的极大似然估计： λ=1s∑Sj=1|δj| λ = 1 s ∑ j = 1 S | δ j | 。

未来转折点是随机取样的，用如下方式进行，来保证转折点的平均频率符合历史分布：

∀j>T,{δj=0δjw.p.Laplace(0,λ)T−STw.p.ST ∀ j > T , { δ j = 0 w . p . T − S T δ j L a p l a c e ( 0 , λ ) w . p . S T

这样就可以设置未来的变化趋势与历史上的变化趋势有相同的频率和幅度，进而测量不确定性。

一旦 λ λ 从数据中推断出以后，我们采用这种生成模型来模拟可能的未来趋势，并用这些模拟出的趋势来计算不确定性的间隔。

3.2 Seasonality
商业活动经常具有多个不同时长的周期性，例如5天的工作日会在每周的数据产生影响，学校的假期也会对每年的数据产生影响。为了拟合并预测这种作用，我们必须制定出季节性模型。

本研究主要依靠傅里叶级数来构造灵活的周期性模型，可以设置P为我们想要的时间序列的规则周期长度（例如，当以天为单位的时间序列，可以对年度数据设置P=365.25，周数据设置P=7）。这样，就得到了任意平滑周期效应的估算值：

s(t)=∑n=1N(ancos(2πntP)+bnsin(2πntP) s ( t ) = ∑ n = 1 N ( a n c o s ( 2 π n t P ) + b n s i n ( 2 π n t P )

为了拟合周期性，需要估计这2N个参数 β=[a1,b1,...,aN,bN] β = [ a 1 , b 1 , . . . , a N , b N ] 。这是通过对历史上和未来的每个t值构建一个季节性向量矩阵来实现的，例如对于每年的周期性，设置N=10，

X(t)=[cos(2π(1)t365.25),...,sin(2π(10)365.25)] X ( t ) = [ c o s ( 2 π ( 1 ) t 365.25 ) , . . . , s i n ( 2 π ( 10 ) 365.25 ) ]

这时，季节性组分为：

s(t)=X(t)β s ( t ) = X ( t ) β

在我们的生成模型中，我们采用 β β ~ Normal(0,σ2) N o r m a l ( 0 , σ 2 ) 来对季节性施加一个先验分布。

将傅里叶级数的项数N进行截断相当于对季节性施加了一个低通滤波器，增加N能够提高拟合效率，但是会有过拟合的风险。对于年和周的季节性，我们发现N=10和N=3效果最好。这些参数的选择能够通过模型选择程序例如AIC来自动实现。

3.3 Holidays and Events
节假日和重要事件会对很多商业事件序列产生重要影响，这些的作用通常是可以预测的，但是由于它们的周期性不固定，使得它们不能通过周期性模型来实现。例如，美国感恩节是11月的第四个星期四，超级碗在每年一月或二月的一个周日，很难用程序来确定，还有很多亚洲国家的农历节日等。这些特定节假日对时间序列的影响在每年通常都是类似的，把它们考虑进模型中非常重要。

整理出一个过去和未来事件的列表，指出事件和节假日的名字，如图3所示。

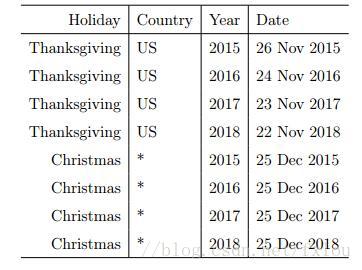
图3 节假日和重要事件列表

直接认为节假日的作用是独立的，将这个列表考虑进模型中，对于每个节假日 i i ，让 Di D i 设置为过去和未来节假日的集合。添加一个指示函数来表明时间 t t 是否在节假日 i i 中，并对每个节假日设定一个参数 κi κ i ，来对应出预测中的变化。与季节性模型处理方法类似，生成一个回归元的矩阵：

Z(t)=[1(t∈D1),...,1(t∈DL)] Z ( t ) = [ 1 ( t ∈ D 1 ) , . . . , 1 ( t ∈ D L ) ]

设置

h(t)=Z(t)κ h ( t ) = Z ( t ) κ

与季节性模型类似，采用先验 κ κ ~ Normal(0,ν2) N o r m a l ( 0 , ν 2 ) 。

实际上，节假日前后一段时间都会受到影响，因此采用一个时间窗口，并把窗口期都认为是节假日的做法经常被使用。

3.4 Model Fitting
当把季节和节假日特性组合起来放入矩阵 X X 中，转折点指示器 a(t) a ( t ) 放入矩阵A中时，整个模型

y(t)=g(t)+s(t)+h(t)+ϵ y ( t ) = g ( t ) + s ( t ) + h ( t ) + ϵ

可以表达为简单几行Stan代码，如下所示：

model {
// Priors
k ∼ normal(0, 5);
m ∼ normal(0, 5);
epsilon ∼ normal(0, 0.5);
delta ∼ double_exponential(0, tau);
beta ∼ normal(0, sigma);
// Logistic likelihood
y ∼ normal(C ./ (1 + exp(-(k + A * delta) .* (t - (m + A * gamma)))) +
X * beta, epsilon);
// Linear likelihood
y ∼ normal((k + A * delta) .* t + (m + A * gamma) + X * beta, sigma);
}

对模型的拟合采用Stan的L-BFGS来找出最大后验估计，并且可以在考虑模型不确定性的情况下，对未来的不确定性做出完整的后验推断。
图4是采用Prophet模型对facebook事件时间序列进行的预测结果，Prophet模型能够预测周和年的周期性，而且不会在2014年年初有过激的反应。在第一个预测中，有过拟合的现象，这是由于只有一年的训练数据。在第三个预测中，模型还没有学习趋势的变化。

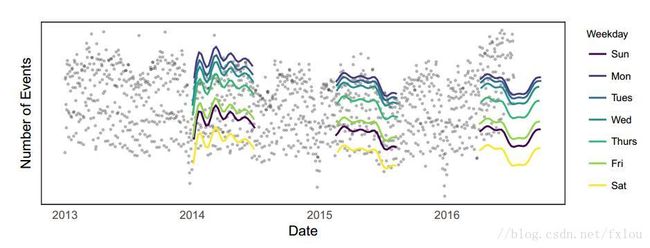图4 Prophet模型预测结果
图5为预测模型学习了近3个月的数据后的预测结果，表现出了趋势的变化（实线部分）。
图5 Prophet模型采用所有可用的数据进行训练，包括对历史数据的插值。实线为样本内的拟合情况，虚线为样本外的预测。

可分解模型的一个重要特点是，可以看到预测模型的各个组成部分，图6展示了图5预测模型趋势，周的季节性，年的季节性成分。这就为分析人员深入理解预测问题提供了有力的工具，而不只是简单地做出预测。

图6 图5中Prophet预测模型的成分

Stan程序中参数 tau t a u 和 sigma s i g m a 分别用于控制模型中转折点和季节性的正则化程度。正则化参数对防止过拟合很重要，但是很难有足够多的历史数据来通过交叉验证选择出最佳的正则化参数。我们对大部分预测问题选取默认值，当需要优化时可以在分析循环过程中完成。