递归和循环
概念
在日常编程中经常会遇到重复计算相同的问题,此时一般会采用递归或者循环来解决。无论是采用递归还是循环,都需要经历如下三步:首先需要找出计算问题的规律,用数学计算公式表达出来;然后再用代码编程来实现这个数学计算公式;最后采用递归或者循环的方式 多次运行这个数学计算公式,从而得出计算结果(为了保证程序的健壮性,往往还需要进行一些边界值处理)。可以看到前两步都是相同,只是第三步到底是选择递归还是循环呢?要回答这个问题,我们首先来看下递归和循环各自的特点。
递归:在一个函数(或者方法)体内调用这个函数自身,直到某个条件满足(否则会一直执行下去,直到栈内存溢出)。
循环:通过设置一个初始值和终止条件,并在这个范围内重复计算。
下面通过一个简单的示例来展示递归和循环(以下示例都是java编写)。
示例:一个整数数组内所有成员的和
这是日常编程中经常遇到的、也是很简单的计算问题。比如:知道一个网站每天的pv,要统计一周内总pv,已知一周内每天的pv是一个数组{1231,2001,1874,1203,3030,2020,1122}。下面的分别以循环和递归进行实现:
/**
* 循环实现
* @param array
* @return
*/
public int addArarry1(int [] array){
int count= 0;
if(array == null|| array.length<=0){
return count;
}
for(int i=0;i /**
* 递归实现
* @param array
* @param len
* @return
*/
public int addArray2(int[] array,int len){
if(array == null|| len<=0){
return 0;
}
return array[len-1] + addArray2(array,len-1);
}
从这个简单的示例可以看出,递归实现的代码更加简洁,可阅读性也更强。但为什么在日常开发中,我们经常看到的是第一种循环实现,而非递归实现呢?这可能是因为,读书时期老师说过能用循环尽量不要用递归。这种说法也是有道理的,因为递归调用方法自身 是有额外的开销的。这里以java例,来分析递归。
Java的vm栈和递归
我们都知道在java的每个线程中,jvm都为其分配一个vm栈的内存空间(可以通过-Xss调整这个栈的大小)。在该线程中的很次方法调用,都会分配一个栈帧,并在该方法调用结束后自动释放栈帧。但在递归调用过程中,每次方法的调用都依赖下一次方法调用结果,在下一个方法返回之前,方法不会结束,也就是说栈帧不能被释放,如下: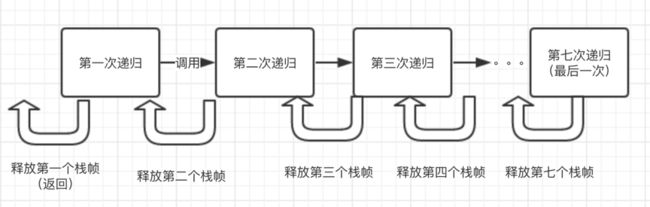
这里只是模拟了上一个示例中对7个数进行递归相加,会进行7次递归方法调用,产生7个栈帧,并且只有在最后一次方法调用完成后,这7个栈帧才会被依次释放。
这也就是vm栈的由来,我们都知道栈是后进先出。递归的过程,其实就是依次把 栈帧压入vm栈,直到最后一个栈帧入栈,然后再依次出栈。上一个示例中的数组只有7个数,如果有上万个数,就会有一万个栈帧先入栈,然后再出栈, 而vm栈的空间是有限的(比如512k,通过-Xss设置),此时可能就会出现栈内存溢出。
这就是java中递归调用的本质(其他编程语言的本质也大致类似),这也就是老师为什么说在能用循环的情况下不要用递归。其中一个原因就是如果递归层次太深,有可能出现栈内存溢出。还有另外一个原因就是递归有可能出现重复计算,从而导致效率低下。比如下一个示例:
斐波那契数列
要求输出第N项斐波那契树。首先回忆下老师过的斐波那契数,用f(n)表示第n个斐波那契数:当n=0时,f(n)=0 ;当n=1时f(n)=1;当n>1时,f(n)=f(n-1)+f(n-2)。这里公式已经列出来了,如果用递归实现,代码非常简洁,如下:
public int fibonacci1(int n){
if(n<=0){
return 0;
}
if(n==1){
return 1;
}
return fibonacci1(n-1)+fibonacci1(n-2);
}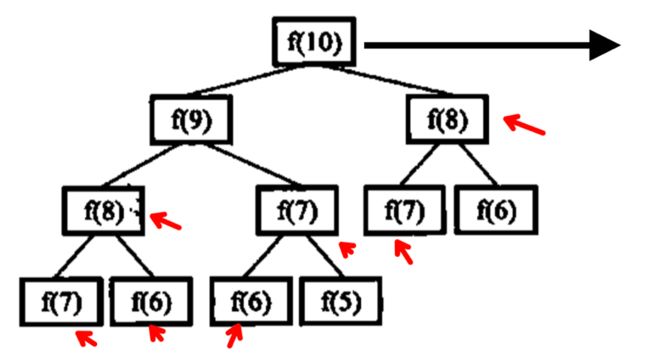
可以看到有很多的重复计算,比如在计算f(10)时,需要计算f(8);而在计算f(9)时又需要计算f(8),依次类推,就会发现有很多重复计算,尤其是在n较大的时候,使用递归来实现斐波那契数的效率愈发低下。
此时我们想到的就是如何把已经计算的值保存下来,防止重复计算。这里可以用一个辅助空间,比如一个HashMap,把计算过的值存储下来,在下次使用时先查询是否已经计算过,如果已经计算过就直接使用,否则再计算。此时就需要一个额外的容量为n的HashMap辅助空间,增加了空间复杂度,这个HashMap中保存了从1到n项的斐波拉契数。
就这个问题而已,我们不需要保存所有的n项斐波那契数,而是只需要返回第n项即可。此时采用循环实现,就会更加简单,首先根据f(0)和f(1)可以计算出f(2);再根据f(1)和f(2)又可以计算出f(3), 以此类推就可以计算出f(n)。具体实现如下:
/**
* 循环实现斐波那契
* @param n
* @return
*/
public long fibonacci2(int n) {
long result=0;
long pre1=0;
long pre2=1;
if(n==0) {
return pre1;
}
if(n==1) {
return pre2;
}
for (int i = 2; i <= n; i++) {
result = pre1+pre2;
//移动指针
pre1 = pre2;
pre2 = result;
}
return result;
}总结
通过上述分析,我们可以看出使用递归 可以是代码更简洁,并且有更好的可读性;但可能出现栈内存溢出,以及重复计算这两个问题。回到文章开头的问题,使用递归还是循环,我们该如何选择呢?存在就是有道理的,不应该像老师说的尽量不用递归。而是应该根据实际情况,在递归深度不超过1000(我的笔记本在超过3000多时出现栈内存溢出,当然可以通过-Xss适当调大栈内存);并且如果使用递归没有重复计算的情况下,我们就可以优先选择递归。还是那句话,因为递归可以使我们的代码看起来更加优雅。
写这篇博客的目的不是为了批判递归,而是让大家更深入的了解递归,并在适当的时候拥抱递归。