题目:一个二维数组,二维数组中的每个数都是正数,要求从左上角走到右下角,每一步只能向右或者向下,沿途经过的数字要累加起来,返回最小路径和.
就题目举个例子:给定二维矩阵arr如下:
1,2,3,4
2,5,6,7
2,3,4,5
该二维矩阵的最小路径为:1,2,2,3,4,5,最小路径和为:17。
思路一:暴力递归
处于位置(i,j)时,只能向右或者向下走,于是想到递归解决,代码具体含义见注释,代码如下:
/**
* 题目: 一个二维数组,二维数组中的每个数都是正数,要求从左上角走到右下角,每一步只能向右或者向下.
* 沿途经过的数字要累加起来,返回最小路径和.
*/
public static int findMinPath(int[][] arr) {
/**
* 暴力递归
*/
return process(arr, 0, 0);
}
public static int process(int[][]arr, int i, int j) {
/**
* process返回从第(i,j)个位置到右下角时最短路径
*/
//baseCase (i,j)为右下角
if(i==arr.length-1&&j==arr[0].length-1) return arr[i][j];
//到达最后一行时
else if(i==arr.length-1) return arr[i][j] + process(arr, i, j+1);
//到达最后一列时
else if(j==arr.length-1) return arr[i][j] + process(arr, i+1, j);
//普通位置
else return arr[i][j] + Math.min(process(arr, i+1, j), process(arr, i, j+1));
}
思路二:记忆化搜索
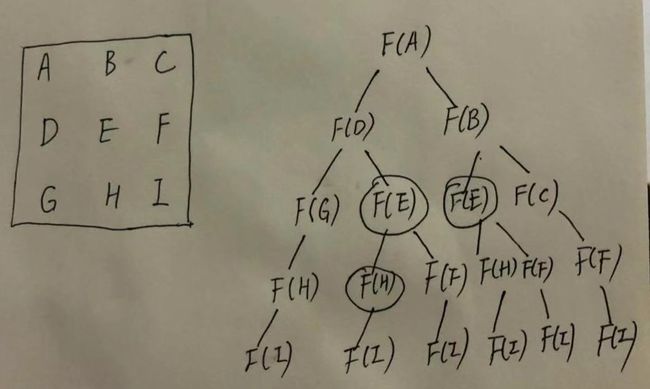
暴力递归不记录每一个子问题的解,每次需要用到的时候再次递归,时间复杂度很高,于是,我们想把子问题的解记录下来,避免重复计算,举个例子,假如二维矩阵arr如下:
a,b,c
d,e,f
g,h,i
暴力递归如下图所示(画图软件不咋会呢,拍了照片,哈哈),其中,有很多重复计算,比如画圈的地方。
因此,在返回递归结果前,先记录到哈希表,相应的,下次递归之前,先查表,代码如下:
static Map cache = new HashMap<>();
public static int findMinPath1(int[][] arr) {
/**
* 记忆化搜索:在暴力递归的基础上加一个缓存机制,递归之前先查哈希表,免去不必要的递归
*/
return process1(arr, 0, 0);
}
private static int process1(int[][] arr, int i, int j) {
//baseCase,
int res = 0;
if (i==arr.length-1&& j==arr[0].length-1) {
res = arr[i][j];
}
//(i,j)为最后一行的点
else if(i==arr.length-1) {
if(cache.containsKey(i+","+(j+1))) {
res = arr[i][j] + cache.get(i+","+(j+1));
}
else res = arr[i][j] + process1(arr, i, j+1);
}
//(i,j)为最后一列的点
else if(j==arr[0].length-1) {
if(cache.containsKey((i+1)+","+j)) {
res = arr[i][j] + cache.get((i+1)+","+j);
}
else res = arr[i][j] + process1(arr, i+1, j);
}
//普通位置
else {
int down = 0;
int right = 0;
if(cache.containsKey((i+1)+","+j)) down = cache.get((i+1)+","+j);
else down = process1(arr,i+1,j);
if (cache.containsKey(i+","+(j+1))) right = cache.get(i+","+(j+1));
else right = process1(arr,i,j+1);
res = arr[i][j] + Math.min(down, right);
}
cache.put(i+","+j,res);
return res;
}
思路三:动态规划
根据暴力递归函数,返回值依赖于i和j两个变量,而0=
2、根据递归函数可以求出dp表的最后一行和最后一列;
3、有了2中的值后,dp表中其他位置从右往左、从下往上依次计算即可。
代码如下:
public static int findMinPath2(int[][]arr) {
/**
* 由递归优化成动态规划
*/
int row = arr.length;
int col = arr[0].length;
int[][] dp = new int[row][col];
dp[row-1][col-1] = arr[row-1][col-1];
//计算dp最后一行的值
for (int j=col-2;j>=0;j--) {
dp[row-1][j] = dp[row-1][j+1]+ arr[row-1][j];
}
//计算dp最后一列的值
for(int i=row-2;i>=0;i--) {
dp[i][col-1] = arr[i][col-1] + dp[i+1][col-1];
}
//计算其他位置的值
for(int i=row-2;i>=0;i--) {
for(int j=col-2;j>=0;j--) {
dp[i][j] = arr[i][j] + Math.min(dp[i+1][j],dp[i][j+1]);
}
}
return dp[0][0];
}