最临近、双线性、三次卷积插值算法比较
最临近、双线性、三次卷积插值算法比较
插值算法对于缩放比例较小的情况是完全可以接受的,令人信服的。一般的,缩小0.5倍以上或放大3.0倍以下,对任何图像都是可以接受的。常用的插值方法有:最近邻插值法,双线性插值法,三次卷积插值法。
1.最近邻插值法(Nearest Neighbor Interpolation)
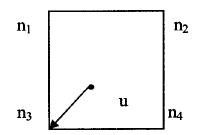
最近邻插值法又称零阶插值,该方法取距离输出图像上的像素点映射到输入图像上的位置最近的输入像素的颜色值(或灰度值)作为输出图像上像素点的颜色值(或灰度值)。如图1所示,最近邻插值法直接计算输出像素映射到输入图像坐标系下的点u和近邻四点(n1,n2,n3,n4)之间的距离,取距离u最近的像素点的颜色值(或灰度值)赋给u。
g(x',y')=f(int(x十0.5),int(y+0.5)) -------------------(1)
公式(1)为最近邻插值的具体计算公式。其中g(x',y')为输出图像中坐标为(x',y')的像素点的颜色值(或灰度值),f(x,y)为输入图像中坐标为(x,y)的像素点的颜色值(或灰度值),(x,y)为输出图像上的坐标(x',y')映射到输入图像坐标系下的坐标。int(x)为取整运算。
2.双线性插值法(Bilinear Interpolation)
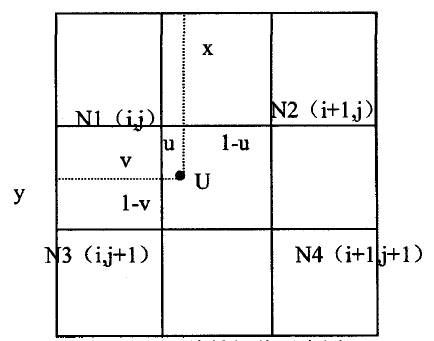
双线性插值法又称一阶插值,利用输入图像中与输出图像像素点映射位置最邻近的4个像素点的颜色值(或灰度值)计算输出图像中像素点的颜色值(或灰度值)。如图2所示。
图2中,假设输出图像上的一个像素点g(x',y')其坐标为(x',y'),它映射到输入图像中的点u其坐标为(x,y)。n1,n2,n3,n4为与点u最邻近的四个点,其坐标分别为(i,j),(i+1,j),(i,j+1),(i+1,j+1),颜色值(或灰度值)分别为f(i,j),f(i+1,j),f(i,j+1),f(i+1,j+1)。则双线性插值的计算公式为公式(2),其中u=(x-i),v=(y-j)。
g(x',y')=(1-u)(1-v)f(i,j) + u(1-v)f(i+1,j) + (1-u)vf(i,j+1) + uvf(i+1,j+1) ---------------(2)
3.三次卷积插值法
为了得到更精确的(x',y')的颜色值(或灰度值)g(x',y'),就不仅需要考虑与(x',y')点最邻近的四个点对它的影响,还要考虑到该点周围16个相邻点的颜色值(或灰度值)对它的影响。如图3所示。
由连续信号采样定理可知,若对采样值用插值函数s(x)=sin(πx)/(πx)插值,则可以准确地恢复原函数,也就是说可以准确地得到采样点间任意点的值"三次卷积插值法实质上就是利用一个三次多项式来近似理论上最佳插值函数S(x),如公式(3)。
目的像素值f(i+u,j+v)可由如下插值公式得到:
f(i+u,j+v) = [A] * [B] * [C]
其中:
[A]=[ S(u + 1) S(u + 0) S(u - 1) S(u - 2) ]
┏ f(i-1, j-1) f(i-1, j+0) f(i-1, j+1) f(i-1, j+2) ┓
[B]=┃ f(i+0, j-1) f(i+0, j+0) f(i+0, j+1) f(i+0, j+2) ┃
┃ f(i+1, j-1) f(i+1, j+0) f(i+1, j+1) f(i+1, j+2) ┃
┗ f(i+2, j-1) f(i+2, j+0) f(i+2, j+1) f(i+2, j+2) ┛
┏ S(v + 1) ┓
[C]=┃ S(v + 0) ┃
┃ S(v - 1) ┃
┗ S(v - 2) ┛
不同的插值方法,具有不同的特点和优缺点"最邻近插值法计算简单,工作量小,但处理后的图像边缘容易产生锯齿效应造成图像的不连续;三次卷积插值法带有边缘增强的效果,能够较好的保持图像的细微结构,但计算量很大;双线性插值法克服了最邻近法不连续的缺点,计算较三次卷积法简单,但边缘受到平滑作用出现轮廓模糊现象。