积分图(一) - 原理及应用
积分图原理
第一个提出 Haar 特征快速计算方法的是 CVPR2001上 的那篇经典论文 [《Rapid object detection using a boosted cascade of simple features》] (http://www.cs.utexas.edu/~grauman/courses/spring2007/395T/papers/viola_cvpr2001.pdf), Viola 提出了一种利用积分图(integral image)快速计算 Haar 特征的方法, 这个方法使得图像的局部矩形求和运算的复杂度从 O(MN) 下降到了 O(4) 。
Haar 特征的计算需要重复计算目标区域的像素值,使用积分图能大大减少计算量,达到实时计算 Haar 特征的目的。简单来说,就是先构造一张“积分图”(integral image),也叫 Summed Area Table,之后任何一个 Haar 矩形特征都可以通过查表的方法(Look Up Table)和有限次简单运算得到,大大减少了运算次数。所以但凡需要重复计算目标区域内像素值和的场合,积分图都能派上用场。下面开始介绍积分图原理,并给出其的几个应用。
1、积分图原理
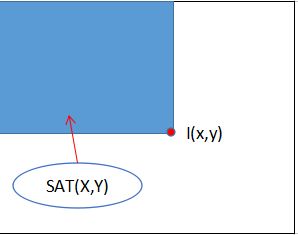
图像是由一系列的离散像素点组成, 因此图像的积分其实就是求和. 图像积分图中每个点的值是原图像中该点左上角的所有像素值之和.
首先建立一个数组 A 作为积分图像,其宽高与原图像相等. 然后对这个数组赋值,每个点存储的是该点与图像原点所构成的矩形中所有像素的和:
\[\begin{equation}\begin{aligned} SAT(x, y) = \sum_{x_i \leq x, y_i \leq y}{I(x_i, y_i)} \end{aligned}\end{equation}\]
其中 \(I(x,y)\) 表示图像 (x,y) 位置的像素值。积分图像可以采用增量的方式计算:
\[\begin{equation}\begin{aligned} SAT(x, y) = SAT(x, y-1) + SAT(x-1, y) - SAT(x-1, y-1) + I(x,y) \end{aligned}\end{equation}\]
初始边界:$ SAT(-1,y) = SAT(x,-1) = SAT(-1,-1) = 0 $
为了更好地说明这个等式,下面我用几幅图来说明:
图1.坐标(x,y)处在原图像中示例
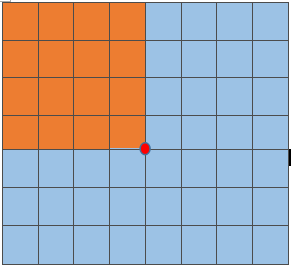
图2.坐标(x,y-1)处的积分图像SAT(x,y-1)示例
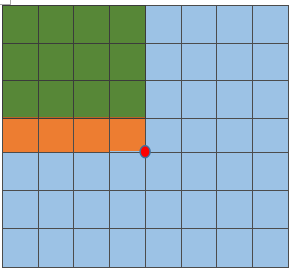
图3.坐标(x-1,y)处的积分图像SAT(x-1,y)示例
图4.坐标(x-1,y-1)处的积分图像SAT(x-1,y-1)示例
可以看到,\(SAT(x,y-1)+SAT(x,y-1)\) 后,有一部分重合的区域,即 \(SAT(x-1,y-1)\),所以需减掉,最后还需要将当前坐标(x,y)的像素值\(I(x,y)\)包含进来。
定义了积分图的概念,就可以很方便的计算任意区域内的像素和,如下图所示:
积分图数组初始化之后, 我们就得到了一张积分图:
点1的积分 \(SAT_1=Sum(Ra)\),
点2的积分 \(SAT_2=Sum(Ra)+Sum(Rb)\),
点3的积分 \(SAT_3=Sum(Ra)+Sum(Rc)\),
点4的积分 \(SAT_4=Sum(Ra)+Sum(Rb)+Sum(Rc)+Sum(Rd)\)
那么为了计算某个矩形像素和,比如区域 Rd 内所有点的像素值之和(积分)可以表示为:
\[\begin{equation}\begin{aligned} Sum(Rd)=SAT_1+SAT_4-SAT_2-SAT_3 \end{aligned}\end{equation}\]
所以无论矩形的尺寸大小,只需查找积分图像 4 次就可以快速计算任意矩形内像素值的和, 即算法复杂度为 O(4)。
2、积分图应用
2.1 Haar-like特征值计算
以如下一种 Haar-like 边缘特征为例
假设需要计算的这种 Haar-like 特征在图中的位置如下所示:
那么,A,B区域所构成的 Haar-like 边缘特征是:
\[\begin{equation}\begin{aligned} Harr_{A-B} &= Sum(A) - Sum(B) \\ &= [SAT_4+SAT_1-SAT_2-SAT_3] - [SAT_6+SAT_3-SAT_4-SAT_5] \end{aligned}\end{equation}\]
显然,对一个灰度图而言,事先将其积分图构建好,当需要计算灰度图某个区域内所有像素点的像素值之和的时候,利用积分图,通过查表运算,可以迅速得到结果。
2.2 使用积分图像实现自适应阈值化
自适应阈值是一种局部方法。它的原理是根据每个像素的邻域(如 5x5)计算阈值,如将每个像素的值与指定的邻域的平均值进行比较,如果某像素的值与它的局部平均值差别很大,就会被当作异常值在阈值化过程中被分离。
如若不采用积分图像,则每个像素比较时,都需要进行 5 x 5 次加法运算;而采用积分图像,运算复杂度不随邻域大小而改变,每次只需计算 2 次加法和 2 次减法。
2.3 Boxfilter 快速计算
积分图可以使复杂度为O(MN)的求和, 求方差等运算降低到O(1)或近似于O(1)的复杂度,但它的缺点是不支持多尺度。
Boxfilter 的原理有点类似 Integral Image,而且比它还要快,但是实现步骤比较复杂。在计算矩形特征之前,Boxfilter 与 Integral Image 都需要对图像进行初始化(即对数组A赋值), 不同于 Integral Image, Boxfilter 的数组 A 中的每个元素的值是该像素邻域内的像素和(或像素平方和), 在需要求某个矩形内像素和的时候,直接访问数组中对应的位置就可以了。因此可以看出它的复杂度是O(1)。
Boxfilter 的细节可以移步这里.
2.4 滑动窗口
其实就是上面的 Boxfilter 中使用的方法.
我本人在做车牌字符分割时,设计了一个动态模板在车牌图像上滑动,并且每次滑动都计算一次模板内包含的非零像素点个数,没用积分图的时候,每次计算都要遍历,效率真的太低,滑动 1000 多次,计算耗时竟达到了几百 ms,这在实时处理中是不能容忍的。而后去补了积分图的知识,使用积分图来计算每次滑动后区域内的非零像素点个数,效率不要太高,只耗费了几 ms 就完事了。深深感叹算法的博大精深!
参考
[1]: 积分图原理及应用
[2]: 极限优化:Haar特征的另一种的快速计算方法—boxfilter
[3]: Viola–Jones, object detection framework--Rapid Object Detection using a Boosted Cascade of Simple Features中文翻译 及 matlab 实现(见文末链接)