线性回归(2)缩减系数理解
摘要:
当我们的数据特征比样本点还多怎么办,是否能够预测呢答案是否定。
岭回归
那么如何解决这个问题呢?科学家们引入了岭回归这个概念,岭回归其实就是如下:
与前面的算法相比。这里通过预测误差的最小化得到系数首先抽取一部分用于训练I的系数,剩下的再来训练W
def ridgeRegres(xMat,yMat,lam=0.2):
xTx = xMat.T*xMat
denom = xTx +eye(shape(xMat)[1])*lam
if linalg.det(denom)==0.0:
print "this matrix is singular"
return
ws = denom.I*(xMat.T*yMat)
return ws
def ridgeTest(xArr,yArr):
xMat = mat(xArr);yMat = mat(yArr).T
yMean = mean(yMat,0)
xMeans = mean(xMat,0)
xVar = var(xMat,0)
xMat = (xMat-xMeans)/xVar
numTestPtS = 30
wMat = zeros((numTestPtS,shape(xMat)[1]))
for i in range(numTestPtS):#lamda is different
ws = ridgeRegres(xMat,yMat,exp(i-10))
wMat[i,:] = ws.T
return wMat
reload(regression)
abX,abY = regression.loadDataSet('abalone.txt')
ridgeWeights = regression.ridgeTest(abX,abY)
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(ridgeWeights)
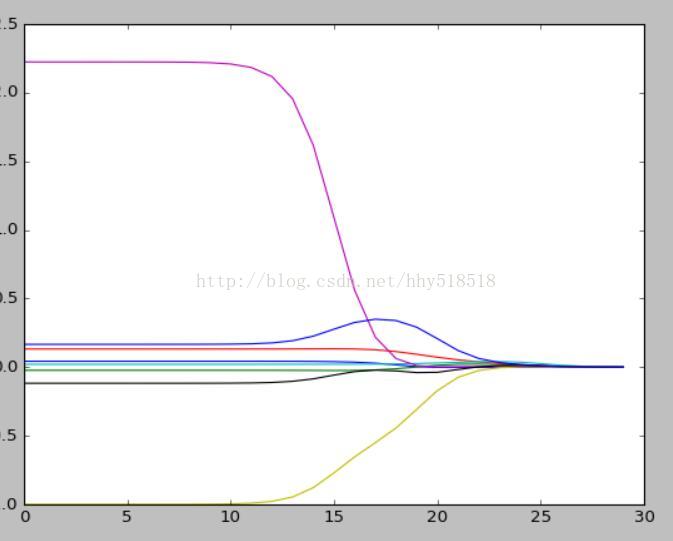
plt.show()我们绘制出Lambda的图形
我们可以看到最左边的时候Lambda最小的时候系数和原来的线性回归的系数是一样的,当增大的过程中,系数会慢慢趋近于0.所以需要在中间部分找到最佳的
作为参数变量。
LASSO
通过增加约数最小二乘可以得到和岭回归一样的公式:
虽然约束条件只是稍微变换但是约束形式确实大相径庭,在这个Lambda足够小的时候,可以帮助我们更好理解数据
前向逐步回归算法
这个算法和lasso算法效果差不都。属于一种贪心算法,就是每一步尽可能减小误差,一开始的时候权重都为1,每一步的决策就是权重增加或者减小一个很小的值
数据标准化,分布都满足0均值和单位方差
每轮迭代
队当前最小误差lowestErrror为正无穷
队每个特征
增大或者减小
改变一个系数得到新的W
计算这个W下的误差
如果error小于最小误差,更新
我们得到的程序如下:
def rssError(yArr,yHatArr): #yArr and yHatArr both need to be arrays
return ((yArr-yHatArr)**2).sum()
def regularize(xMat):#regularize by columns
inMat = xMat.copy()
inMeans = mean(inMat,0) #calc mean then subtract it off
inVar = var(inMat,0) #calc variance of Xi then divide by it
inMat = (inMat - inMeans)/inVar
return inMat
def stageWise(xArr,yArr,eps=0.01,numIt=100):
xMat = mat(xArr);yMat = mat(yArr).T
yMean = mean(yMat,0)
yMat = yMat - yMean
xMat = regularize(xMat)
m,n = shape(xMat)
returnMat = zeros((numIt,n))
ws = zeros((n,1));wsTest = ws.copy();wsMax = ws.copy();
for i in range(numIt):
print ws.T
lowestError = inf;
for j in range(n):
for sign in [-1,1]:
wsTest = ws.copy();
wsTest[j]+=eps*sign;
yTest = xMat*wsTest;
rssE = rssError(yMat.A,yTest.A)
if rssE下面用这个算法进行效果测试
reload(regression) xArr,yArr = regression.loadDataSet('abalone.txt') regression.stageWise(xArr,yArr,0.01,200)
为什么使用这个算法呢?这个算法的好处就是当构建一个模型以后,我们通过这个算法找出重要的特征,可以及时停止对不重要特征的收集,最后如果用于测试
那么可以每100次迭代以后构建一个模型,10折交叉方法最终选择最小误差的模型。
权衡偏差和方差
任何时候模型和测量值都有差异,当考虑模型的噪声的时候。还需要考虑噪声的来源。测量过程本身也有噪声问题,我们举一个例子如果下面数据来源如下图
降低核的复杂度就是需要拟合的参数越少,那么训练误差越小,一般认为误差由三个部分产生,偏差,方差以及随机噪声
我们前面的方法缩减法就是通过减小预测误差。而方差就是可以度量的,选取随机样本来进行拟合,再取另外一组拟合,系数的差异大小就是方差大小
实例分析:预测乐高玩具价格
乐高公司对每个乐高玩具包含的部件数目从10件到5000件不等。我们需要用回归技术建立一个预测模型
步骤如下:
1)收集数据:Google shopping的API收集
2)准备数据:返回JSON数据抽取价格
3)分析数据:可视化分析
4)训练算法:构建不同的模型,采用逐步线性回归和直接线性回归
5)测试算法:交叉验证不同类型,分析哪个模型好
6)使用算法
收集数据这里不多说就是调用库并JSON解析
def searchForSet(retX, retY, setNum, yr, numPce, origPrc):
sleep(10)
myAPIstr = 'AIzaSyD2cR2KFyx12hXu6PFU-wrWot3NXvko8vY'
searchURL = 'file:///E:/pythonProject/ML/LinearRegrossion/setHtml/?key=%s&country=US&q=lego+%d&alt=json' % (myAPIstr, setNum)
pg = urllib2.urlopen(searchURL)
retDict = json.loads(pg.read())
for i in range(len(retDict['items'])):
try:
currItem = retDict['items'][i]
if currItem['product']['condition'] == 'new':
newFlag = 1
else: newFlag = 0
listOfInv = currItem['product']['inventories']
for item in listOfInv:
sellingPrice = item['price']
if sellingPrice > origPrc * 0.5:
print "%d\t%d\t%d\t%f\t%f" % (yr,numPce,newFlag,origPrc, sellingPrice)
retX.append([yr, numPce, newFlag, origPrc])
retY.append(sellingPrice)
except: print 'problem with item %d' % i
def setDataCollect(retX, retY):
searchForSet(retX, retY, 8288, 2006, 800, 49.99)
searchForSet(retX, retY, 10030, 2002, 3096, 269.99)
searchForSet(retX, retY, 10179, 2007, 5195, 499.99)
searchForSet(retX, retY, 10181, 2007, 3428, 199.99)
searchForSet(retX, retY, 10189, 2008, 5922, 299.99)
建立模型并根据岭回归调节参数
def crossValidation(xArr,yArr,numVal=10):
m = len(yArr)
indexList = range(m)
errorMat = zeros((numVal,30))
for i in range(numVal):
trainX=[];trainY=[]
testX =[];testY=[]
random.shuffle(indexList)
for j in range(m):
if j取其中百分之10为测试集合,同时保留很多误差,取其中最好的误差