EM算法(期望最大化)详细推导
版权声明:博主原创文章,转载请注明来源,谢谢合作!!
https://blog.csdn.net/hl791026701/article/details/84641872
1.简介
期望最大化 (Expectation Maximization) 算法最初是由 Ceppellini 等 人 1950 年在讨论基因频率的估计的时候提出的。后来又被 Hartley 和 Baum 等人发展的更加广泛。目前引用的较多的是 1977 年 Dempster 等人的工作。它主要用于从不完整的数据中计算最大似然估计。后来经过 其他学者的发展,这个算法也被用于聚类等应用。
2.例子
本片博文希望通过一个例子来解释期望最大化的来由及合理性。
我们来考虑一个掷硬币实验:现在我们有两枚硬币A和B,这两枚硬币和普通的硬币不一样,他们投掷出正面的概率和投掷出反面的概率不一定相同。我们将A和B投掷出正面的概率分别记为 θ A \theta _{A} θA和 θ B \theta _{B} θB。我们现在独立地做五次实验:随机的从这两枚硬币中抽取1枚,投掷10次,统计出现正面的次数。那么我们就得到了如下表的实验结果。
| 实验代号 | 投掷的硬币 | 出现正面的次数 |
|---|---|---|
| 1 | B | 5 |
| 2 | A | 9 |
| 3 | A | 8 |
| 4 | B | 4 |
| 5 | A | 7 |
在这个实验中,我们记录两组随机变量 X = ( X 1 , X 2 , X 3 , X 4 , X 5 ) X=(X_{1},X_{2},X_{3},X_{4},X_{5}) X=(X1,X2,X3,X4,X5), Z = ( Z 1 , Z 2 , Z 3 , Z 4 , Z 5 ) Z=(Z_{1},Z_{2},Z_{3},Z_{4},Z_{5}) Z=(Z1,Z2,Z3,Z4,Z5),其中 X i ϵ { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 } X_{i} \epsilon\left \{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 \right \} Xiϵ{1,2,3,4,5,6,7,8,9,10}代表实验 i 中出现的正面次数, Z i ϵ { A , B } Z_{i} \epsilon \left \{ A,B \right \} Ziϵ{A,B}代表这次实验投掷的是硬币A还是硬币B。
我们的目标的通过这个实验来估计 θ = ( θ A , θ B ) \theta = \left ( \theta _{A},\theta _{B} \right ) θ=(θA,θB)的数值。这个实验中的参数估计就是有完整数据的参数估计,这个是因为我们不仅仅知道每次实验中投掷出正面的次数,我们还知道每次实验中投掷的是硬币A还是硬币B。
一个很简单的也很直接的估计 θ \theta θ的方法如下公式所示。
θ A ^ = 用 硬 币 A 投 掷 出 正 面 的 次 数 用 硬 币 A 投 掷 的 次 数 \hat{\theta _{A}} = \frac{用硬币A投掷出正面的次数}{用硬币A投掷的次数} θA^=用硬币A投掷的次数用硬币A投掷出正面的次数
(1) θ B ^ = 用 硬 币 B 投 掷 出 正 面 的 次 数 用 硬 币 B 投 掷 的 次 数 \hat{\theta _{B}} = \frac{用硬币B投掷出正面的次数}{用硬币B投掷的次数} \tag{1} θB^=用硬币B投掷的次数用硬币B投掷出正面的次数(1)
实际上这样的估计就是统计上的极大似然估计(maximum likelihood estimation)的结果。用 P ( X , Z ∣ θ ) P\left ( X,Z\mid \theta \right ) P(X,Z∣θ)来表示X,Z的联合概率分布(其中带有参数 θ)。那么对于上面的实验,我们可以计算出我们观察到的结果即 x 0 = ( 5 , 9 , 8 , 4 , 7 ) x^{0} = \left ( 5,9,8,4,7 \right ) x0=(5,9,8,4,7) , z 0 = ( B , A , A , B , A ) z^{0} = \left ( B,A,A,B,A \right ) z0=(B,A,A,B,A)的概率如下公式(2)。函数 P ( X = x 0 , Z = z 0 ∣ θ ) P\left ( X=x^{0},Z=z^{0}\mid \theta \right ) P(X=x0,Z=z0∣θ)就叫做 θ \theta θ的似然函数。我们将它对 θ \theta θ求偏导并令偏导数为0,就可以得到(1)的结果。
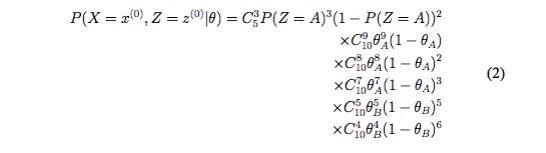
现在我们将这个问题稍微改变一下,我们将我们所观察到的结果修改一下:我们现在只知道每次试验有几次投掷出正面,但是不知道每次试验投掷的 是哪个硬币,也就是说我们只知道表1中第一列和第三列。这个时候我们就 称 Z 为隐藏变量 (Hidden Variable),X 称为观察变量 (Observed Variable)。 这个时候再来估计参数 θ A \theta _{A} θA 和 θ B \theta _{B} θB,就没有那么多数据可供使用了,这个时 候的估计叫做不完整数据的参数估计。
如果我们这个时候有某种方法(比如,正确的猜到每次投掷硬币是 A 还是 B),这样的话我们就可以将这个不完整的数据估计变为完整数据估计。
当然我们如果没有方法来获得更多的数据的话,那么下面提供了一种在 这种不完整数据的情况下来估计参数 θ \theta θ 的方法。我们用迭代的方式来进行:
- 我们先赋给 θ \theta θ一个初始值,这个值不管是经验也好猜的也好,反正我 们给它一个初始值。在实际使用中往往这个初始值是有其他算法的结 果给出的,当然随机给他分配一个符合定义域的值也可以。这里我们 就给定 θ A = 0.7 \theta _{A} = 0.7 θA=0.7, θ B = 0.4 \theta _{B} = 0.4 θB=0.4
- 然后我们根据这个来判断或者猜测每次投掷更像是哪枚硬币投掷的结 果。比如对于试验 1,如果投掷的是 A,那么出现 5 个正面的概率为 C 10 5 × 0. 7 5 × ( 1 − 0. 7 5 ) ≈ 0.1029 C_{10}^{5}\times 0.7^{5}\times \left ( 1-0.7^{5} \right ) \approx 0.1029 C105×0.75×(1−0.75)≈0.1029;如果投掷的是B,出现5个正面的概 率为 C 10 5 × 0. 4 5 × ( 1 − 0. 4 5 ) ≈ 0.2007 C_{10}^{5}\times 0.4^{5}\times \left ( 1-0.4^{5} \right ) \approx 0.2007 C105×0.45×(1−0.45)≈0.2007;基于试验1的试验结果,可以判 断这个试验投掷的是硬币 A 的概率为 0.1029/(0.1029+0.2007)=0.3389, 是 B 的概率为0.2007/(0.1029+0.2007)= 0.6611。因此这个结果更可能 是投掷 B 出现的结果。
- 假设上一步猜测的结果为B,A,A,B,A,那么根据这个猜测,可以像完整数据的参数估计一样(公式2)重新计算 θ \theta θ的值。
这样一次一次的迭代2-3步骤直到收敛,我们就得到了 θ \theta θ的估计值。现在你可能有疑问,这个方法靠谱吗?事实证明,他的确靠谱的。
期望最大化算法就是在这个想法上改进的。他在估计每次投掷的硬币的时候,并不是确定住这次就是硬币A或者B,它计算出来这次投掷的硬币是A的概率和B的概率;然后利用这个概率(或者叫做Z的分布)来计算似然函数。期望最大化算法步骤总结如下:
E 步骤 先利用旧的参数值 θ ′ \theta ^{'} θ′计算隐藏变量Z的(条件)分布 P θ ′ ( Z = z j ∣ X i = x i ) P_{\theta ^{'}}\left ( Z = z_{j}\mid X_{i}=x_{i}\right ) Pθ′(Z=zj∣Xi=xi),然后计算 l o g P θ ( Z , X = x ) 1 logP_{\theta }\left ( Z, X=x\right )^{1} logPθ(Z,X=x)1的期望
(3) E ( l o g P θ ( Z , X = x ) ) = ∑ i = 1 n ∑ j P θ ′ ( Z = z j ∣ X = x i ) l o g P θ ( Z = z j , X i = x i ) E\left ( logP_{\theta } \left ( Z,X=x \right )\right ) = \sum_{i=1}^{n}\sum_{j}^{ }P_{\theta ^{'}}\left ( Z=z_{j}\mid X=x_{i} \right )logP_{\theta }\left ( Z=z_{j},X_{i}=x_{i} \right ) \tag{3} E(logPθ(Z,X=x))=i=1∑nj∑Pθ′(Z=zj∣X=xi)logPθ(Z=zj,Xi=xi)(3)
其中 θ \theta θ是当前的 θ \theta θ值,而 θ ′ \theta ^{'} θ′是上一次迭代得到的 θ \theta θ值。公式3中已经只剩下$\theta $一个变量了, θ ′ \theta^{'} θ′是一个确定的值,这个公式或者函数常常叫做Q函数,用 Q ( θ , θ ′ ) Q\left ( \theta ,\theta ^{'} \right ) Q(θ,θ′)来表示。
M 步骤 极大化Q,往往这一步是求导,得到由旧的 θ \theta θ值 θ ′ \theta ^{'} θ′来计算新的 θ \theta θ值的公式:
(4) ∂ Q ∂ θ = 0 \frac{\partial Q}{\partial \theta } = 0 \tag{4} ∂θ∂Q=0(4)
总结一下,期望最大化算法就是先根据参数初值估计隐藏变量的分布,然后根据影藏变量的分布来计算观察变量的似然函数,估计参数的值。前者通常称为E步骤,后者称为M步骤。
3数学基础
首先来明确一下我们的目标:我们的目标是在观察变量X和给定观察样本 x 1 , x 2 , x 3 . . . x n x_{1},x_{2},x_{3}...x_{n} x1,x2,x3...xn的情况下,极大化对数似然函数
(5) l ( θ ) = ∑ i = 1 n l n P ( X i = x i ) l\left ( \theta \right )=\sum_{i=1}^{n}lnP\left ( X_{i }=x_{i} \right ) \tag{5} l(θ)=i=1∑nlnP(Xi=xi)(5)
其中只包含观察变量的概率密度函数
(6) P ( X i = x i ) = ∑ j P ( X i = x i , Z = z j ) P\left ( X_{i}=x_{i} \right ) =\sum_{j}^{ }P\left ( X_{i}=x_{i},Z=z_{j} \right ) \tag{6} P(Xi=xi)=j∑P(Xi=xi,Z=zj)(6)
其中Z为隐藏随机变量,{ z j z_{j} zj}是Z的所有可能的取值。那么
(7) l ( θ ) = ∑ i = 1 n l n ∑ j P ( X i = x i , Z = z j ) = ∑ i = 1 n l n ∑ j α j P ( X i = x i , Z = z j ) α j l\left ( \theta \right )=\sum_{i=1}^{n}ln\sum_{j}^{ }P\left ( X_{i}=x_{i},Z=z_{j} \right ) \\ =\sum_{i=1}^{n}ln\sum_{j}^{ } \alpha _{j}\frac{P\left ( X_{i}=x_{i},Z=z_{j} \right )}{\alpha _{j}} \tag{7} l(θ)=i=1∑nlnj∑P(Xi=xi,Z=zj)=i=1∑nlnj∑αjαjP(Xi=xi,Z=zj)(7)
- Jensen不等式
这里我们引入了一组参数(不要怕多,我们后面会处理掉他的)$\alpha $,它满足
∀ \forall ∀可能的 j , α j ∈ ( 0 , 1 ] j,\alpha _{j}\in (0,1] j,αj∈(0,1]和$\sum_{j}\alpha _{j} = 1 $到这里,先介绍一个凸函数的性质,或者对 f ( x ) f\left ( x \right ) f(x)为凸函数, ∀ i = 1 , 2 , 3 , . . . , n , λ i ∈ [ 0 , 1 ] , ∑ i = 1 n λ i = 1 \forall i= 1,2,3,...,n,\lambda _{i}\in [0,1],\sum_{i=1}^{n}\lambda _{i}=1 ∀i=1,2,3,...,n,λi∈[0,1],∑i=1nλi=1, 对 f ( x ) f\left ( x \right ) f(x)
定义域的任意n个 x 1 , , x 2 , . . . , x n x_{1,},x_{2},...,x_{n} x1,,x2,...,xn有
(8) f ( ∑ i = 1 n λ i x i ) ≤ ∑ i = 1 n λ i f ( x i ) f\left ( \sum_{i=1}^{n}\lambda _{i}x_{i} \right ) \leq \sum_{i=1}^{ n}\lambda _{i}f\left ( x_{i} \right ) \tag{8} f(i=1∑nλixi)≤i=1∑nλif(xi)(8)
对于严格的凸函数,上面的等号只有在 x 1 = x 2 = . . . = x n x_{1}=x_{2}=...=x_{n} x1=x2=...=xn的时候成立。关于凸函数的其他性质不在赘述。对数函数是一个严格的凸函数。因而我们可以有下面这个结果:
(9) l ( θ ) = ∑ i = 1 n l n ∑ j P ( X i = x i , Z = z j ) ⩾ ∑ i = 1 n ∑ j α j l n P ( X i = x i , Z = z j ) α j l\left ( \theta \right )=\sum_{i=1}^{n}ln\sum_{j}^{ }P\left ( X_{i}=x_{i},Z=z_{j} \right ) \\ \geqslant \sum_{i=1}^{n}\sum_{j}^{ } \alpha _{j}ln\frac{P\left ( X_{i}=x_{i},Z=z_{j} \right )}{\alpha _{j}} \tag{9} l(θ)=i=1∑nlnj∑P(Xi=xi,Z=zj)⩾i=1∑nj∑αjlnαjP(Xi=xi,Z=zj)(9)
现在我们根据等号成立的条件来确定 α j \alpha _{j} αj即
(10) P ( X i = x i , Z = z j ) α j = c \frac{P\left ( X_{i}=x_{i},Z=z_{j} \right )}{\alpha _{j}} =c \tag{10} αjP(Xi=xi,Z=zj)=c(10)
其中c是一个与j无关的常数,因为 ∑ j α j = 1 \sum_{j}^{ }\alpha _{j} =1 ∑jαj=1稍作变换就可以得到
(11) α j = P ( X i = x i , Z = z j ) P ( X i = x i ) \alpha _{j}=\frac{P\left ( X_{i}=x_{i},Z=z_{j} \right )}{P\left ( X_{i}=x_{i} \right )} \tag{11} αj=P(Xi=xi)P(Xi=xi,Z=zj)(11)
现在来解释一下我们得到了什么。 α j \alpha _{j} αj就是 Z = z j Z=z_{j} Z=zj在 X = x j X=x_{j} X=xj下的条件概率或者后验概率。求 α \alpha α就是求隐藏随机变量Z的条件分布。总结一下目前得到的公式就是
(12) l ( θ ) = ∑ i = 1 n ∑ j α j l n P ( X i = x i , Z = z j ) α j l\left ( \theta \right )=\sum_{i=1}^{n}\sum_{j}^{ } \alpha _{j}ln\frac{P\left ( X_{i}=x_{i},Z=z_{j} \right )}{\alpha _{j}} \tag{12} l(θ)=i=1∑nj∑αjlnαjP(Xi=xi,Z=zj)(12)
直接就极大值比较难求,EM算法就是按照下面过程来的。
(1). 根据上一步的 θ \theta θ来计算 α \alpha α,即隐藏变量的条件分布
(2). 极大化似然函数来得到当前的 θ \theta θ的估计
3.1 极大似然估计
在这里博主觉得还是说说极大似然估计吧。给定一个概率分布D,假设其概率分布密度函数为 f f f,其中 f f f是一个带有一组参数 θ \theta θ。为了估计这组参数 θ \theta θ,我们可以从这个分布中抽出一个具有 n n n个采样值的 X 1 , X 2 , . . . , X n , X_{1},X_{2},...,X_{n}, X1,X2,...,Xn,,那么这个就是 n n n个独立同分布随机变量,他们分别有取值 x 1 , x 2 , . . . , x n , x_{1},x_{2},...,x_{n}, x1,x2,...,xn,,那么我们就可以计算出出现这样一组观察值的概率密度为
(13) l ( θ ) = ∏ i = 1 n f ( x i ) l\left ( \theta \right )=\prod_{i=1}^{n}f\left ( x_{i} \right ) \tag{13} l(θ)=i=1∏nf(xi)(13)
对于 f f f是离散的情况,就计算出现这一组观察值的概率
(14) l ( θ ) = ∏ i = 1 n P ( X i = x i ) l\left ( \theta \right )=\prod_{i=1}^{n}P\left ( X_{i}=x_{i} \right ) \tag{14} l(θ)=i=1∏nP(Xi=xi)(14)
注意,这个函数中是含参数 θ \theta θ的, θ \theta θ的极大似然估计就是求让上面似然函数取值极大值的时候参数 θ \theta θ值。
一般来说,会将上面那个似然函数取自然对数,这样往往可以简化计算。记住,这样仅仅是为了简化计算。取了自然对数后的函数就叫做对数似然函数。
(15) l ( θ ) = ∏ i = 1 n l n f ( x i ) l\left ( \theta \right )=\prod_{i=1}^{n}lnf\left ( x_{i} \right ) \tag{15} l(θ)=i=1∏nlnf(xi)(15)
因为对数是一个严格的单调递增的凹函数,所以对数似然函数取极大值与对对数似然函数取得极大值是等价的。
3.2 期望最大化算法收敛
如何保证算法收敛呢?我们只用证明KaTeX parse error: Expected group after '\left' at position 77: …( \theta \left ^̲{\left ( t \rig…就可以了。
(16) l ( θ ( t + 1 ) ) = ∑ i = 1 n ∑ j α j t + 1 l n P ( X = x i , Z = z j t + 1 ) α j t + 1 ≥ ∑ i = 1 n ∑ j α j t l n P ( X = x i , Z = z j t + 1 ) α j t ≥ ∑ i = 1 n ∑ j α j t l n P ( X = x i , Z = z j t ) α j t = l ( θ t ) l\left ( \theta ^{\left ( t +1 \right )} \right ) = \sum_{i=1}^{n}\sum_{j}^{ }\alpha_{j}^{t+1}ln\frac{P\left ( X=x_{i},Z=z_{j}^{t+1} \right )}{\alpha _{j}^{t+1}} \\ \geq \sum_{i=1}^{n}\sum_{j}^{ }\alpha_{j}^{t}ln\frac{P\left ( X=x_{i},Z=z_{j}^{t+1} \right )}{\alpha _{j}^{t}} \\ \geq \sum_{i=1}^{n}\sum_{j}^{ }\alpha_{j}^{t}ln\frac{P\left ( X=x_{i},Z=z_{j}^{t} \right )}{\alpha _{j}^{t}} \\ =l\left ( \theta ^{t} \right ) \tag{16} l(θ(t+1))=i=1∑nj∑αjt+1lnαjt+1P(X=xi,Z=zjt+1)≥i=1∑nj∑αjtlnαjtP(X=xi,Z=zjt+1)≥i=1∑nj∑αjtlnαjtP(X=xi,Z=zjt)=l(θt)(16)
其中第一个大于等于号是因为只有当 θ \theta θ取值合适的时候才有等号成立,第二个大于等于号正是M步骤的操作所致。
这样我们就知道 l ( θ ) l\left ( \theta \right ) l(θ)是随着迭代次数的增加越来越大的,收敛条件是值不再变化或者变化幅度很小。
4 应用举例
4.1 参数估计
很直接的应用就是参数估计,上面举的例子就是参数估计。
4.2 聚类
但是如果估计的参数可以表明类别的话,比如某个参数表示某个样本是
否属于某个集合。这样的话其实聚类问题也就可以归结为参数估计问题。