NLP TASK6 神经网络基础

学习内容

前馈神经网络、网络层数、输入层、隐藏层、输出层、隐藏单元、激活函数的概念。
感知机相关；定义简单的几层网络（激活函数sigmoid），递归使用链式法则来实现反向传播。
激活函数的种类以及各自的提出背景、优缺点。（和线性模型对比，线性模型的局限性，去线性化）
深度学习中的正则化（参数范数惩罚：L1正则化、L2正则化；数据集增强；噪声添加；early stop；Dropout层）、正则化的介绍。
深度模型中的优化：参数初始化策略；自适应学习率算法（梯度下降、AdaGrad、RMSProp、Adam；优化算法的选择）；batch norm层（提出背景、解决什么问题、层在训练和测试阶段的计算公式）；layer norm层。
FastText的原理。
利用FastText模型进行文本分类。

内容笔记

前馈神经网络

前馈网络中各个神经元按接受信息的先后分为不同的组。每一组可以看作
一个神经层。每一层中的神经元接受前一层神经元的输出，并输出到下一层神经元。整个网络中的信息是朝一个方向传播，没有反向的信息传播，可以用一个有向无环路图表示。前馈网络包括全连接前馈网络和卷积神经网络等。其可以看作一个函数，通过简单非线性函数的多次复合，实现输入空间到输出空间的复杂映射。见下图

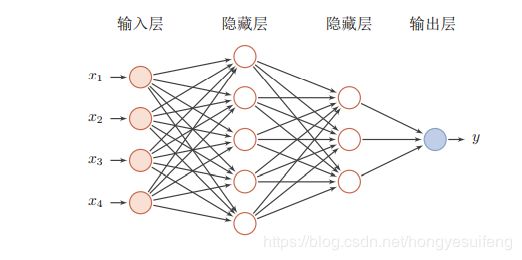
如上图所示前馈神经网络，该网络公有三层结构，通常输入层不计入层数，各层定义见图所示。
激活函数在神经元中也非常重要的。为了增强网络的表示能力和学习能
力，激活函数需要具备以下几点性质：

1. 连续并可导（允许少数点上不可导）的非线性函数。可导的激活函数可以
   直接利用数值优化的方法来学习网络参数。
2. 激活函数及其导函数要尽可能的简单，有利于提高网络计算效率。
3. 激活函数的导函数的值域要在一个合适的区间内，不能太大也不能太小，
   否则会影响训练的效率和稳定性。

后面会详细介绍常用的激活函数。

感知机

感知机（perceptron）是二分类的线性分类模型，属于监督学习算法。原理见下图

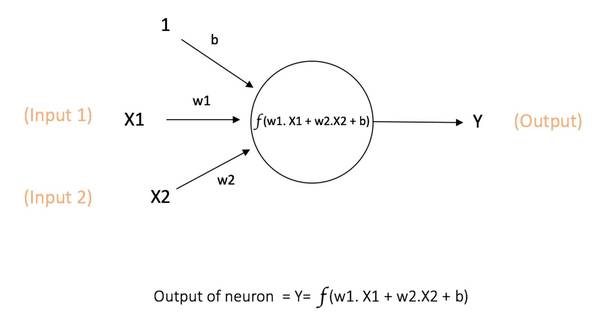
该感知机是通过对输入进行计算，得出中间信号，再和阈值相比看是否输出信号。详细原理见下面的推导：

激活函数

Sigmoid 型激活函数

Sigmoid型函数是指一类S型曲线函数，为两端饱和函数。常用的Sigmoid
型函数有Logistic函数和Tanh函数。

Logistic函数：
$$\sigma (x)=\frac{1}{1+exp(-x)}$$
Logistic函数可以看成是一个“挤压”函数，把一个实数域的输入“挤压”
到(0, 1)。当输入值在0附近时，Sigmoid型函数近似为线性函数；当输入值靠近两端时，对输入进行抑制。输入越小，越接近于0；输入越大，越接近于1。和感知器使用的阶跃激活函数相比，Logistic 函数是连续可导的，其数学性质更好。因为Logistic函数的性质，使得装备了Logistic激活函数的神经元具有以下两点性质:
1）其输出直接可以看作是概率分布，使得神经网络可以更好地和统计学习模型进行结合。
2）其可以看作是一个软性门（Soft Gate），用来控制其它神经元输出信息的数量。

Tanh函数：
Tanh函数是也一种Sigmoid型函数。其定义为
$$tanh(x)=\frac{exp(x)-exp(-x)}{exp(x)+exp(-x)}$$
Tanh函数的输出是零中心化的（Zero-Centered），而Logistic函数的输出恒大于0。非零中心化的输出会使得其后一层的神经元的输入发生偏置偏移（Bias Shift），并进一步使得梯度下降的收敛速度变慢。
还有Hard-Logistic 和 Hard-Tanh 函数，不详细介绍。

修正线性单元

修正线性单元（Rectified Linear Unit，ReLU）也叫rectifier函数，是目前深层神经网络中经常使用的激活函数。ReLU实际上是一个斜坡（ramp）函数，定义为
$$ReLU(x)=\{\begin{array}{ll}x,& \text{if x≥0}\\ 0,& \text{if x<0 }\end{array}=max(0,x)$$
优点采用 ReLU 的神经元只需要进行加、乘和比较的操作，计算上更加高效。ReLU函数被认为有生物上的解释性，比如单侧抑制、宽兴奋边界（即兴奋程度也可以非常高）。Sigmoid型激活函数会导致一个非稀疏的神经网络，而ReLU却具有很好的稀疏性，大约50%的神经元会处于激活状态。在优化方面，相比于Sigmoid型函数的两端饱和，ReLU函数为左饱和函数，且在x > 0时导数为1，在一定程度上缓解了神经网络的梯度消失问题，加速梯度下降的收敛速度。
缺点 ReLU 函数的输出是非零中心化的，给后一层的神经网络引入偏置偏移，会影响梯度下降的效率。此外，ReLU神经元在训练时比较容易“死亡”。在训 ReLU 神经元指采用 ReLU练时，如果参数在一次不恰当的更新后，第一个隐藏层中的某个ReLU神经元在 作为激活函数的神经元。
所有的训练数据上都不能被激活，那么这个神经元自身参数的梯度永远都会是0，在以后的训练过程中永远不能被激活。这种现象称为死亡ReLU问题
（ReLU Problem），并且也有可能会发生在其它隐藏层。 在实际使用中，为了避免上述情况，有几种ReLU的变种也会被广泛使用。

带泄露的 ReLU：
带泄露的ReLU在输入 x < 0时，保持一个很小的梯度λ。这样当神经元非激活时也能有一个非零的梯度可以更新参数，避免永远不能被激活。带泄露的ReLU的定义如下：
$$LeakyReLU(x)=\{\begin{array}{ll}x,& \text{if x>0}\\ \gamma x,& \text{if x≤0}\end{array}=max(0,x)+\gamma min(0,x)$$
通常$\gamma$是一个很小的常数，比如0.01。
还有带参数的 ReLU，ELU，Softplus 函数等

Swish 函数是一种自门控（Self-Gated）激活函数。

Maxout单元也是一种分段线性函数。

总之激活函数使得网络能提供非线性化，为模型的拟合提供了更多的可能，而不只是线性模型的叠加操作。

深度学习中的正则化

数据增强：
数据增强是提升算法性能、满足深度学习模型对大量数据的需求的重要工具。数据增强通过向训练数据添加转换或扰动来人工增加训练数据集。数据增强技术如水平或垂直翻转图像、裁剪、色彩变换、扩展和旋转通常应用在视觉表象和图像分类中。

L1 和 L2 正则化：
L1 和 L2 正则化是最常用的正则化方法。L1 正则化向目标函数添加正则化项，以减少参数的绝对值总和；而 L2 正则化中，添加正则化项的目的在于减少参数平方的总和。根据之前的研究，L1 正则化中的很多参数向量是稀疏向量，因为很多模型导致参数趋近于 0，因此它常用于特征选择设置中。机器学习中最常用的正则化方法是对权重施加 L2 范数约束。
L1正则化定义为：

L2正则化定义为：

Dropout:
Bagging 是通过结合多个模型降低泛化误差的技术，主要的做法是分别训练几个不同的模型，然后让所有模型表决测试样例的输出。而 Dropout 可以被认为是集成了大量深层神经网络的 Bagging 方法，因此它提供了一种廉价的 Bagging 集成近似方法，能够训练和评估值数据数量的神经网络。
Dropout 指暂时丢弃一部分神经元及其连接。随机丢弃神经元可以防止过拟合，同时指数级、高效地连接不同网络架构。神经元被丢弃的概率为 1 − p，减少神经元之间的共适应。隐藏层通常以 0.5 的概率丢弃神经元。使用完整网络（每个节点的输出权重为 p）对所有 2^n 个 dropout 神经元的样本平均值进行近似计算。Dropout 显著降低了过拟合，同时通过避免在训练数据上的训练节点提高了算法的学习速度。

早停法:
早停法可以限制模型最小化代价函数所需的训练迭代次数。早停法通常用于防止训练中过度表达的模型泛化性能差。如果迭代次数太少，算法容易欠拟合（方差较小，偏差较大），而迭代次数太多，算法容易过拟合（方差较大，偏差较小）。早停法通过确定迭代次数解决这个问题，不需要对特定值进行手动设置。

深度模型中的优化

梯度下降方法：
常见的深度学习模型中的优化学习方法有梯度下降方法，随机梯度下降方法，小批量下降方法等。该方法的原理都是先定义一个损失函数，然后求得使得该损失函数变化最快的方向最为参数的迭代方向，准确来说只有一个使函数上升最快的方向，这个方向由梯度给出，与之相反的方向就是下降最快的方向。这就是算法名称的来源，我们沿着梯度的方向进行下降，所以就叫做梯度下降。区别就是每次选取计算迭代的数据量的不同，分为梯度下降，批梯度下降，随机梯度下降等。

动量（Momentum）
随机梯度下降和小批量梯度下降是机器学习中最常见的优化技术，然而在大规模应用和复杂模型中，算法学习的效率是非常低的。而动量策略旨在加速学习过程，特别是在具有较高曲率的情况下。动量算法利用先前梯度的指数衰减滑动平均值在该方向上进行回退 [26]。该算法引入了变量 v 作为参数在参数空间中持续移动的速度向量，速度一般可以设置为负梯度的指数衰减滑动平均值。对于一个给定需要最小化的代价函数，动量可以表达为：

其中 α 为学习率，γ ∈ (0, 1] 为动量系数，v 是速度向量，θ是保持和速度向量方向相同的参数。一般来说，梯度下降算法下降的方向为局部最速的方向（数学上称为最速下降法），它的下降方向在每一个下降点一定与对应等高线的切线垂直，因此这也就导致了 GD 算法的锯齿现象。虽然 SGD 算法收敛较慢，但动量法是令梯度直接指向最优解的策略之一。在实践中，γ初始设置为 0.5，并在初始学习稳定后增加到 0.9。同样，α 一般也设置地非常小，因为梯度的量级通常是比较大的。

Nesterov 加速梯度（NAG）:
Nesterov 加速梯度（NAG）和经典动量算法非常相似，它是一种一阶优化算法，但在梯度评估方面有所不同。在 NAG 中，梯度的评估是通过速度的实现而完成的。NAG 根据参数进行更新，和动量算法一样，不过 NAG 的收敛速度更好。在批量梯度下降中，与平滑的凸函数相比，NAG 的收敛速度超出 1/k 到 1/(k^2) [27]。但是，在 SGD 中，NAG 无法提高收敛速度。NAG 的更新如下：

动量系数设置为 0.9。经典的动量算法先计算当前梯度，再转向更新累积梯度。相反，在 NAG 中，先转向更新累积梯度，再进行校正。其结果是防止算法速度过快，且增加了反应性（responsiveness）。

Adagrad:
Adagrad 亦称为自适应梯度（adaptive gradient），允许学习率基于参数进行调整，而不需要在学习过程中人为调整学习率。Adagrad 根据不常用的参数进行较大幅度的学习率更新，根据常用的参数进行较小幅度的学习率更新。因此，Adagrad 成了稀疏数据如图像识别和 NLP 的天然选择。然而 Adagrad 的最大问题在于，在某些案例中，学习率变得太小，学习率单调下降使得网络停止学习过程。在经典的动量算法和 Nesterov 中，加速梯度参数更新是对所有参数进行的，并且学习过程中的学习率保持不变。在 Adagrad 中，每次迭代中每个参数使用的都是不同的学习率。

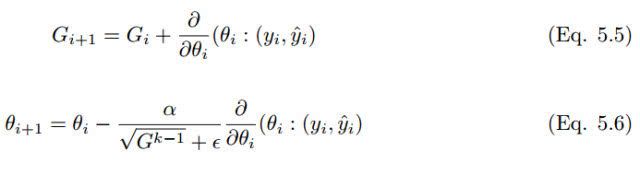
其他AdaDelta，RMS prop，Adam等优化算法，详见：
https://www.jiqizhixin.com/articles/2017-12-20
https://zhuanlan.zhihu.com/p/32626442

优化算法的选择：
如果数据是稀疏的，就用自适用方法，即 Adagrad, Adadelta, RMSprop, Adam。
RMSprop, Adadelta, Adam 在很多情况下的效果是相似的。
Adam 就是在 RMSprop 的基础上加了 bias-correction 和 momentum，
随着梯度变的稀疏，Adam 比 RMSprop 效果会好。
整体来讲，Adam 是最好的选择。
很多论文里都会用 SGD，没有 momentum 等。SGD 虽然能达到极小值，但是比其它算法用的时间长，而且可能会被困在鞍点。

Batch Norm层

背景：
    在深度学习中，由于问题的复杂性，我们往往会使用较深层数的网络进行训练，尤其是对深层神经网络的训练调参更是困难且复杂。在这个过程中，需要去尝试不同的学习率、初始化参数方法（例如Xavier初始化）等方式来帮助我们的模型加速收敛。深度神经网络之所以如此难训练，其中一个重要原因就是网络中层与层之间存在高度的关联性与耦合性。网络中层与层之间的关联性会导致如下的状况：随着训练的进行，网络中的参数也随着梯度下降在不停更新。一方面，当底层网络中参数发生微弱变化时，由于每一层中的线性变换与非线性激活映射，这些微弱变化随着网络层数的加深而被放大（类似蝴蝶效应）；另一方面，参数的变化导致每一层的输入分布会发生改变，进而上层的网络需要不停地去适应这些分布变化，使得我们的模型训练变得困难，上述这一现象叫做Internal Covariate Shift。
    Batch Normalization的原论文作者给了Internal Covariate Shift一个较规范的定义：在深层网络训练的过程中，由于网络中参数变化而引起内部结点数据分布发生变化的这一过程被称作Internal Covariate Shift。Internal Covariate Shift带来的问题：
（1）上层网络需要不停调整来适应输入数据分布的变化，导致网络学习速度的降低。
（2）网络的训练过程容易陷入梯度饱和区，减缓网络收敛速度。

那么如何减缓Internal Covariate Shift？
ICS产生的原因是由于参数更新带来的网络中每一层输入值分布的改变，并且随着网络层数的加深而变得更加严重，因此我们可以通过固定每一层网络输入值的分布来对减缓ICS问题。
（1）白化（Whitening）
白化（Whitening）是机器学习里面常用的一种规范化数据分布的方法，主要是PCA白化与ZCA白化。白化是对输入数据分布进行变换，进而达到以下两个目的：
1使得输入特征分布具有相同的均值与方差。其中PCA白化保证了所有特征分布均值为0，方差为1；而ZCA白化则保证了所有特征分布均值为0，方差相同；
2去除特征之间的相关性。
通过白化操作，我们可以减缓ICS的问题，进而固定了每一层网络输入分布，加速网络训练过程的收敛。
（2）Batch Normalization提出
然后白化有以下两个问题：

计算成本太高，并且在每一轮训练中的每一层我们都需要做如此高成本计算的白化操作；
白化过程改变了网络每一层的分布，因而改变了网络层中本身数据的表达能力。底层网络学习到的参数信息会被白化操作丢失掉。
既然有了上面两个问题，一方面，我们提出的normalization方法要能够简化计算过程；另一方面又需要经过规范化处理后让数据尽可能保留原始的表达能力。于是就有了简化+改进版的白化——Batch Normalization。

原理：
该算法本质原理就是这样：在网络的每一层输入的时候，又插入了一个归一化层，也就是先做一个归一化处理，然后再进入网络的下一层。

训练阶段的BN：

测试阶段的BN计算：

Layer Norm层

LN也是对输出归一化的。LN也是为了消除各层的covariate shift，加快收敛速度。LN相对于BN就简单多了。

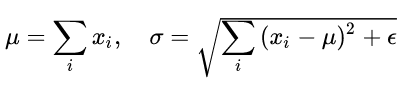
它在training和inference时没有区别，只需要对当前隐藏层计算mean and variance就行
不需要保存每层的moving average mean and variance
不受batch size的限制，可以通过online learning的方式一条一条的输入训练数据
LN可以方便的在RNN中使用
LN增加了gain和bias作为学习的参数，μ和σ分别是该layer的隐层维度的均值和方差

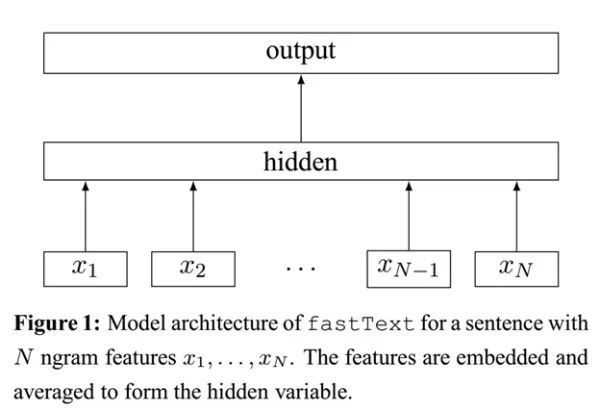
FastText的原理

字符级别的n-gram：
word2vec把语料库中的每个单词当成原子的，它会为每个单词生成一个向量。这忽略了单词内部的形态特征，比如：“apple” 和“apples”，“达观数据”和“达观”，这两个例子中，两个单词都有较多公共字符，即它们的内部形态类似，但是在传统的word2vec中，这种单词内部形态信息因为它们被转换成不同的id丢失了。
为了克服这个问题，fastText使用了字符级别的n-grams来表示一个单词。对于单词“apple”，假设n的取值为3，则它的trigram有:
“”
其中，<表示前缀，>表示后缀。于是，我们可以用这些trigram来表示“apple”这个单词，进一步，我们可以用这5个trigram的向量叠加来表示“apple”的词向量。
这带来两点好处：

1. 对于低频词生成的词向量效果会更好。因为它们的n-gram可以和其它词共享。
2. 对于训练词库之外的单词，仍然可以构建它们的词向量。我们可以叠加它们的字符级n-gram向量。

模型架构：

Fasttext文本分类范例

数据样例

fasttext_train.txt，fasttext_test.txt数据格式：

import fasttext
import os
classifier = fasttext.supervised('fasttext_train.txt', 'fasttext.model', label_prefix='__label__')
result = classifier.test('fasttext_test.txt')
print(result.precision)
print(result.recall)

总结

深度学习很多知识点暂时缺乏时间，所以对各个知识点理解不够深入，仅从表面原理上面进行一定了解，需要进一步深入理解，需要结合实践分析。

参考文献

邱锡鹏：《神经网络与深度学习》
https://blog.csdn.net/hongyesuifeng/article/details/79251390
https://www.jiqizhixin.com/articles/2017-12-20
https://www.jiqizhixin.com/articles/071502
http://ruder.io/optimizing-gradient-descent/index.html#whichoptimizertochoose
https://blog.csdn.net/aliceyangxi1987/article/details/73210204
《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》
https://blog.csdn.net/hjimce/article/details/50866313
https://zhuanlan.zhihu.com/p/34879333
https://www.cnblogs.com/guoyaohua/p/8724433.html
https://blog.csdn.net/c9Yv2cf9I06K2A9E/article/details/79283702