Tensorflow实现Triplet Loss

声明：

1. 翻译自Triplet Loss and Online Triplet Mining in TensorFlow

Triplet Loss

在人脸识别中，Triplet loss被用来进行人脸嵌入的训练。如果你对triplet loss很陌生，可以看一下吴恩达关于这一块的课程。Triplet loss实现起来并不容易，特别是想要将它加到tensorflow的计算图中。

通过本文，你讲学到如何定义triplet loss，和进行triplets采样的几种策略。然后我将解释如何在TensorFlow中使用在线triplets挖掘来实现Triplet loss。

Triplet loss和triplets挖掘

为什么不用softmax

谷歌的论文FaceNet: A Unified Embedding for Face Recognition and Clustering最早将triplet loss应用到人脸识别中。他们提出了一种实现人脸嵌入和在线triplet挖掘的方法，这部分内容我们将在后面章节介绍。

在监督学习中，我们通常都有一个有限大小的样本类别集合，因此可以使用softmax和交叉熵来训练网络。但是，有些情况下，我们的样本类别集合很大，比如在人脸识别中，标签集很大，而我们的任务仅仅是判断两个未见过的人脸是否来自同一个人。

Triplet loss就是专为上述任务设计的。它可以帮我们学习一种人脸嵌入，使得同一个人的人脸在嵌入空间中尽量接近，不同人的人脸在嵌入空间中尽量远离。

定义损失

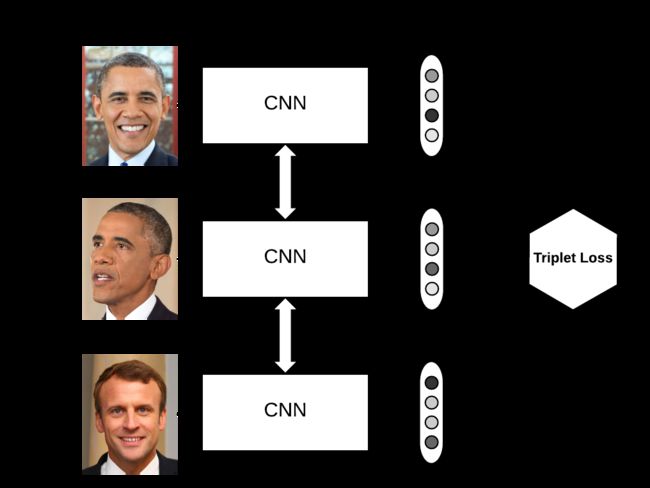
Triplet loss的目标：

• 使具有相同标签的样本在嵌入空间中尽量接近
• 使具有不同标签的样本在嵌入空间中尽量远离

值得注意的一点是，如果只遵循以上两点，最后嵌入空间中相同类别的样本可能collapse到一个很小的圈子里，即同一类别的样本簇中样本间的距离很小，不同类别的样本簇之间也会偏小。因此，我们加入间隔(margin)的概念——跟SVM中的间隔意思差不多。只要不同类别样本簇简单距离大于这个间隔就阔以了。

Triplet可以理解为一个三元组，它由三部分组成：

• anchor在这里我们翻译为原点
• positive同类样本点（与原点同类）
• negative异类样本点

我们要求，在嵌入空间 d d 中，三元组 (a,p,n) ( a , p , n ) 满足一下关系：

L=max(d(a,p)−d(a,n)+margin,0) L = m a x ( d ( a , p ) − d ( a , n ) + m a r g i n , 0 )

最小化该 L L ，则 d(a,p)→0, d(a,n)>margin d ( a , p ) → 0 ,   d ( a , n ) > m a r g i n 。

Triplets挖掘

基于前文定义的Triplet loss，可以将三元组分为一下三个类别：

• easy triplets：可以使loss = 0的三元组，即容易分辨的三元组
• hard triplets： d(a,n)<d(a,p) d ( a , n ) < d ( a , p ) 的三元组，即一定会误识别的三元组
• semi-hard triplets： d(a,p)<d(a,n)<d(a,p)+margin d ( a , p ) < d ( a , n ) < d ( a , p ) + m a r g i n 的三元组，即处在模糊区域（关键区域）的三元组

图中，a为原点位置，p为同类样本例子，不同颜色表示的区域表示异类样本分布于三元组类别的关系

显然，中间的Semi-hard negatives样本对我们网络模型的训练至关重要。

离线和在线triplets挖掘

在网络训练中，应尽可能使用Semi-hard negatives样本，这一节将介绍如何选择这些样本。

离线

可以在每轮迭代之前从所有triplet中选择semi-hard Triplet。也就是先对所有的训练集计算嵌入表达(feature)，然后只选择semi-hard triplets并以此为输入训练一次网络。

因为每轮训练迭代之前都要遍历所有triplet，计算它们的嵌入，所以offline挖掘triplet效率很低。

在线

关于在线挖掘的更详细的解释见博客OpenFace 0.2.0。

假设有B个图片（不是Triplet），也就是可以生成B个嵌入表达，那么我们最多以此生成 B3 B 3 个Triplet，当然大多数Triplet都不符合要求（不满足一个同类一个异类的条件）。

如上图所示，网络输入B个图片，经过CNN得到embedding向量，在从中挑选semi-hard triplet。与离线挖掘相比，在线的方式有两个优点：

• 只遍历一个batch的图片
• 在tansorflow计算图中寻找semi-hard样本

在线挖掘策略

在线挖掘实际上是从图片的嵌入表示中生成Triplet。

对于包含B个图片的banch，设 i,j,k∈[1,B] i , j , k ∈ [ 1 , B ] ，一个合格的Triplet要求：

• 样本i， j不是同一个图片且类别相同
• 样本i, k类别不同

现在的问题就是如何从合格的Triplet中挑选semi-hard Triplet。

假设包含B个图片的banch有P个不同的人组成，没人有K个图片，即 B=PK B = P K 。以K=4为例，有两种在线挖掘策略：

• batch all：选择所有合格的Triplet，对其中的hard和semi-hard Triplet的损失取均值
  
  • 这里的关键在于消除easy Triplet的影响，因为easy Triplet的loss = 0，会拉低平均值
  • 合格的Triplet的数目为 PK(K−1)(PK−K) P K ( K − 1 ) ( P K − K ) ，即PK个原点，K-1个同类样本，PK-K个异类样本
• batch hard：遍历所有原点(也就是banch中的所有样本），选择hardest同类样本( d(a,p) d ( a , p ) 最大的样本)，选择hardest异类样本( d(a,n) d ( a , n ) 最小的样本）
  
  • 一共有PK个Triplet

虽然论文中说这种Triplet的选择策略会大大提高模型的识别效果，但具体结果好坏还是取决于你的数据集。

简单实现triplet loss

使用离线挖掘的策略，简单实现以下Triplet loss如下：

anchor_output = ...  # shape [None, 128]
positive_output = ...  # shape [None, 128]
negative_output = ...  # shape [None, 128]

d_pos = tf.reduce_sum(tf.square(anchor_output - positive_output), 1)
d_neg = tf.reduce_sum(tf.square(anchor_output - negative_output), 1)

loss = tf.maximum(0.0, margin + d_pos - dneg)
loss = tf.reduce_mean(loss)

进阶实现triplet loss

值得一提的是，在TensorFlow中有可以直接滴啊用的Triplet loss实现tf.contrib.losses.metric_learning.triplet_semihard_loss()。在本文中我们不用这个。

计算距离矩阵

计算距离的例子：
输入的嵌入空间向量banch为：

⎡⎣⎢e1e2e3⎤⎦⎥ [ e 1 e 2 e 3 ]

其中， e1 e 1 表示第一个嵌入向量， e2 e 2 表示第二个嵌入向量， e3 e 3 表示第三个嵌入向量，这些向量的特征维度设为4，即 e1=[e11,e12,e13,e14] e 1 = [ e 1 1 , e 2 1 , e 3 1 , e 4 1 ]

根据 ||ei−ej||2 | | e i − e j | | 2 计算嵌入向量之间的距离为：

⎡⎣⎢<e1,e1><e2,e2><e3,e3><e1,e1><e2,e2><e3,e3><e1,e1><e2,e2><e3,e3>⎤⎦⎥−2⋅⎡⎣⎢<e1,e1><e2,e1><e3,e1><e1,e2><e2,e2><e3,e2><e1,e3><e2,e3><e3,e3>⎤⎦⎥+⎡⎣⎢<e1,e1><e1,e1><e1,e1><e2,e2><e2,e2><e2,e2><e3,e3><e3,e3><e3,e3>⎤⎦⎥ [ < e 1 , e 1 > < e 1 , e 1 > < e 1 , e 1 > < e 2 , e 2 > < e 2 , e 2 > < e 2 , e 2 > < e 3 , e 3 > < e 3 , e 3 > < e 3 , e 3 > ] − 2 ⋅ [ < e 1 , e 1 > < e 1 , e 2 > < e 1 , e 3 > < e 2 , e 1 > < e 2 , e 2 > < e 2 , e 3 > < e 3 , e 1 > < e 3 , e 2 > < e 3 , e 3 > ] + [ < e 1 , e 1 > < e 2 , e 2 > < e 3 , e 3 > < e 1 , e 1 > < e 2 , e 2 > < e 3 , e 3 > < e 1 , e 1 > < e 2 , e 2 > < e 3 , e 3 > ]

def _pairwise_distances(embeddings, squared=False):
    """
    计算嵌入向量之间的距离
    Args:
        embeddings: 形如(batch_size, embed_dim)的张量
        squared: Boolean. True->欧式距离的平方，False->欧氏距离
    Returns:
        piarwise_distances: 形如(batch_size, batch_size)的张量
    """
    # 嵌入向量点乘，输出shape=(batch_size, batch_size)
    dot_product = tf.matmul(embedding, tf.transpose(embeddings)

    # 取dot_product对角线上的值，相当于是每个嵌入向量的L2正则化，shape=(batch_size,)
    square_norm = tf.diag_part(dot_product)

    # 计算距离,shape=(batch_size, batch_size)
    # ||a - b||^2 = ||a||^2 - 2 + ||b||^2
    # PS: 下面代码计算的是||a - b||^2，结果是一样的
    distances = tf.expand_dims(square_norm, 0) - 2.0 * dot_product + tf.expand_dims(square_norm, 1)

    # 保证距离都>=0
    distances = tf.maximum(distances, 0.0)

    if not squared:
        # 加一个接近0的值，防止求导出现梯度爆炸的情况
        mask = tf.to_float(tf.equal(distances, 0.0))
        distances = distances + mask * 1e-16

        distances = tf.sqrt(distances)

        # 校正距离
        distances = distances * (1.0 - mask)
    return distances

batch all全局策略

1. 输入一个banch的嵌入向量，shape=(batch_size, embding_dim)
2. 使用_pairwise_distances()获取该batch中嵌入向量间的欧氏距离
3. 计算triplet_loss
4. 使用函数_get_triplet_mask()获取该batch中合格的Triplet
5. 去掉loss<=0的Triplet，这些被称为easy Triplet
6. 对剩余Triplet的loss取均值

先介绍_get_triplet_mask()，再介绍batch_all_triplet_loss()

def _get_triplet_mask(labels):
    """
    Return a 3D mask where mask[a, p, n] is True iff the triplet (a, p, n) is valid.
    A triplet (i, j, k) is valid if:
        - i, j, k are distinct
        - labels[i] == labels[j] and labels[i] != labels[k]
    Args:
        labels: tf.int32 `Tensor` with shape [batch_size]
    """
    # i, j, k分别是不同的样本索引
    indices_equal = tf.cast(tf.eye(tf.shape(labels)[0]), tf.bool)
    indices_not_equal = tf.logical_not(indices_equal)
    i_not_equal_j = tf.expand_dims(indices_not_equal, 2)
    i_not_equal_k = tf.expand_dims(indices_not_equal, 1)
    j_not_equal_k = tf.expand_dims(indices_not_equal, 0)

    distinct_indices = tf.logical_and(tf.logical_and(i_not_equal_j, i_not_equal_k), j_not_equal_k)

    # Check if labels[i] == labels[j] and labels[i] != labels[k]
    label_equal = tf.equal(tf.expand_dims(labels, 0), tf.expand_dims(labels, 1))
    i_equal_j = tf.expand_dims(label_equal, 2)
    i_equal_k = tf.expand_dims(label_equal, 1)

    valid_labels = tf.logical_and(i_equal_j, tf.logical_not(i_equal_k))

    # combine the two masks
    mask = tf.logical_and(distinct_indices, valid_labels)
    return mask

上面代码中的空间逻辑转换可能比较难懂，建议画一个3维图来辅助思考。

def batch_all_triplet_loss(labels, embeddings, margin, squared=False):
    """
    计算整个banch的Triplet loss。
    生成所有合格的triplets样本组，并只对其中>0的部分取均值
    Args: 
        labels: 标签，shape=(batch_size,)
        embeddings: 形如(batch_size, embed_dim)的张量
        margin: Triplet loss中的间隔
        squared: Boolean. True->欧氏距离的平方，False->欧氏距离
    Returns: 
        triplet_loss: 损失
    """
    # 获取banch中嵌入向量间的距离矩阵
    pairwise_dist = _pairwise_distances(embeddings, squared=squared)

    anchor_positive_dist = tf.expand_dims(pairwise_dist, 2)
    anchor_negative_dist = tf.expand_dims(pairwise_dist, 1)

    # 计算一个形如(batch_size, batch_size, batch_size)的3D张量
    triplet_loss = anchor_positive_dist - anchor_negative_dist + margin

    # 将invalid Triplet置零
    # label(a) != label(p) or label(a) == label(n) or a == p
    mask = _get_triplet_mask(labels)
    mask = tf.to_float(mask)
    triplet_loss = tf.multiply(mask, triplet_loss)

    # 删除负值
    triplet_loss = tf.maximum(triplet_loss, 0.0)

    # 计算正值
    valid_triplets = tf.to_float(tf.greater(triplet_loss, 1e-16))
    num_positive_triplets = tf.reduce_sum(valid_triplets)
    num_valid_triplets = tf.reduce_sum(mask)
    fraction_positive_triplets = num_positive_triplet / (num_valid_triplets + 1e-16)

    triplet_loss = tf.reduce_sum(triplet_loss) / (num_positive_triplets + 1e-16)
    return triplet_loss, fraction_positive_triplets

batch hard复杂样本策略

在这种策略下，我们要找到最难区分的同类样本和异类样本。

Hardest positive

1. 获取所有的valid同类样本对(a, p)
2. 选取距离最大的同类样本对

Hardest negative
与获取hardest positive样本，相似

1. 获取所有valid异类样本对
2. 选取距离最小的异类样本对

在选取距离最小的异类样本对时，应当注意，此处与上面选取Hardest positive的策略不同。
如果继续沿用将合格样本对*1，将不合格样本对*0的办法，则距离最小的异类样本对就是0，显然不合理。
下面使我们采用的解决方案：

• 为每个非一类样本对的距离加一个大值
• 这个大值可以使每一个anchor对应样本对中的最大距离

获取hard样本后，用它们的距离计算Triplet loss：triplet_loss = tf.maximum(hardest_positive_dist - hardest_negative_dist + margin, 0.0)

def _get_anchor_positive_triplet_mask(labels):
    """
    返回一个2D掩码，掩码用于筛选合格的同类样本对[a, p]。合格的要求是：a和p是不同的样本索引，a和p具有相同的标签。
    Args:
        labels: tf.int32 形如[batch_size]的张量
    Returns:
        mask: tf.bool 形如[batch_size]的张量
    """
    # i和j是不同的
    indices_equal = tf.cast(tf.eye(tf.shape(labels)[0]), tf.bool)
    indices_not_equal = tf.logical_not(indices_equal)

    # label[i] == label[j]
    labels_equal = tf.equal(tf.expand_dims(labels, 0), tf.expand_dims(labels, 1))

    # 合并
    mask = tf.logical_and(indices_not_equal, labels_equal)
    return mask

类似的，_get_anchor_negative_triplet_mask()不在介绍。

def batch_hard_triplet_loss(labels, embeddings, margin, squared=False):
    """
    为该batch计算Triplet loss
    遍历所有样本，将其作为原点anchor，获取hardest同类和一类样本，构建一个Triplet
    """
    # 获得一个2D的距离矩阵，表示嵌入向量之间的欧氏距离
    pairwise_dist = _pairwise_distances(embeddings, squared=squared)

    # 合格的同类样本距离
    mask_anchor_positive = _get_anchor_positive_triplet_mask(labels)
    mask_anchor_positive = tf.to_float(mask_anchor_positive)
    anchor_positive_dist = tf.multiply(mask_anchor_positive, pairwise_dist)

    # 对每行取最大距离，每行表示每个anchor，输出shape=(batch_size, 1)
    hardest_positive_dist = tf.reduce_max(anchor_positive_dist, axis=1, keepdims=True)

    # 合格的异类样本距离矩阵的掩码
    mask_anchor_negative = _get_anchor_negative_triplet_mask(labels)
    mask_anchor_negative = tf.to_float(mask_anchor_negative)

    # 获取每个anchor下的嵌入向量样本对的最大距离
    max_anchor_negative_dist = tf.reduce_max(pairwise_dist, axis=1, keepdims=True)
    # 不合格的negative嵌入向量样本对距离都要在原来的基础上 + 上面的max_anchor_negative_dist
    anchor_negative_dist = pairwise_dist + max_anchor_negative_dist * (1.0 - mask_anchor_negative)
    # 在每行选择最小距离
    hardest_negative_dist = tf.reduce_min(anchor_negative_dist, axis=1, keepdims=True)

    triplet_loss = tf.maximum(hardest_positive_dist - hardest_negative_dist + margin, 0.0)

    triplet_loss = tf.reduce_mean(triplet_loss)
    return triplet_loss

Resources

github项目地址