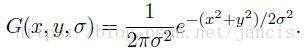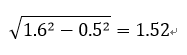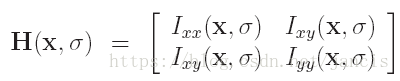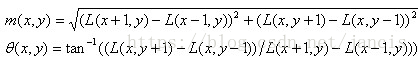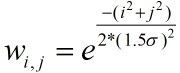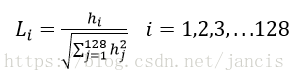自己看SIFT(尺度不变特征变换)算法的一点总结
这是第一次写博客,感觉写个总结会有利于自己对算法的理解
首先,本文参考的博文如下:
1、https://blog.csdn.net/hit2015spring/article/details/52895367(高斯滤波,有利于对生成高斯差分尺度空间的理解)
2、https://blog.csdn.net/abcjennifer/article/details/7639681(目前看到的在博客中点赞数最多的)
3、https://blog.csdn.net/zddblog/article/details/7521424
4、https://blog.csdn.net/kyu_saku/article/details/52804265(一些基本概念)
5、https://blog.csdn.net/u011028345/article/details/70829766(帮助对SIFT特征点描述子生成的理解)
6、https://www.cnblogs.com/JiePro/p/sift_3.html(对理解特征点方向分配很有帮助)
7、https://blog.csdn.net/lingyunxianhe/article/details/79063547(这篇把SIFT算法的整个过程描述的很清楚)
8、原版的英文文献:Distinctive Image Features from Scale-Invariate Keypoints
SIFT是特征点邻域高斯图像梯度统计结果的一种表示,是一种图像局部特征提取算法。
SIFT对于旋转,尺度缩放,亮度变化保持不变性
插一句:为什么要提取图像的局部特征?因为:变量越少,观察结果变化的可能性就越小。
SIFT算法分为以下五个过程:
一、尺度空间的搭建;
二、尺度空间中候选极值点的检测;
三、对上一过程中得出的候选极值点进行筛选,去除低对比度的点和不稳定的边缘响应点,得到真正的特征点;
四、特征点方向分配;
五、特征点描述。
下面对每一个过程进行详细的介绍:
一、尺度空间的搭建
在图像处理中引入一个尺度的概念:它可以模拟人在距离目标由近到远的过程中,目标在视网膜当中形成图像的过程。尺度越大,表示图像的概貌,只能看清楚物体的轮廓,简单的说就是看起来越模糊,相当于我们观察远处的物体;尺度越小,表示图像的细节,相当于我们观察近处的物体。如果需要识别出包含不同尺寸的同一物体的两幅图像,随着物体在图像中大小发生变化,属于该物体的局部区域的大小也会发生变化。SIFT算法中采用图像金字塔的方法就可以解决这一问题,首先将两幅图像想象成是连续的,分别以它们作为底面作四棱椎,就像金字塔一样,那么每一个截面都与原图像相似,且两个金字塔中必然会有包含大小一致的物体的截面,但构造的金字塔层数是离散的,只能构造有限层,所以构造层数越多越好,但处理时间会增加,层数太少也不行,因为向下采样的截面中可能找不到尺寸大小一致的两个物体的图像。
在SIFT算法中,采用的是高斯差分金字塔(DOG),具体为什么是高斯差分金字塔不知道,只知道大牛们通过实验得出:尺度归一化的高斯拉普拉斯算子能够得到最稳定的图像特征,但因为计算量太大,而高斯差分函数与高斯拉普拉斯算子很相似,所以通过高斯差分函数来近似的计算图像最稳定的特征。
首先介绍一下高斯金字塔再来理解高斯差分金字塔,高斯金字塔并不是一个金字塔,而是有很多组(Octave)金字塔构成,并且每组金字塔都包含若干层(Interval),高斯金字塔主要是为了得到不同尺度的图像来模拟图像数据的多尺度特征,构建主要分两步:(1)模糊尺度的确定;(2)降采样。大牛们不知道为了什么原因先对原始图像进行扩大一倍的处理(用双线性插值),应该是为了获得更多的特征点,将其作为高斯金字塔的第1组第1层,将第1组第1层图像经高斯卷积之后作为第1组金子塔的第2层,高斯卷积函数为(高斯卷积核是实现尺度变换的唯一线性核):
上面的高斯卷积函数只是一个数学表达式,根据数学理论知识,由于数字图像是离散的,想求导和求最值这些操作都是使用滤波器,在图像处理中通过卷积滤波实现对图像的平滑,它使用正态分布(高斯函数)计算模糊模板,并使用该模板与原图像做卷积运算,达到模糊图像的目的。
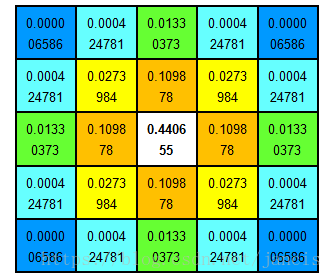
二维高斯卷积模板如下:
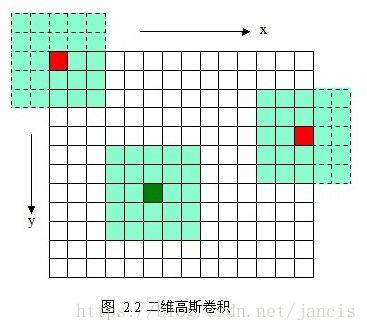
将二维高斯卷积模板与图像作卷积运算过程如下:
分布不为0的像素组成的卷积矩阵与原始图像作变换,每个像素的值都是周围相邻像素值的加权平均,原始像素的值有最大的高斯分布值,所以有最大的权重,相邻像素随着距离原始像素越来越远,其权重也越来越小,这样进行模糊处理比其他的均衡模糊滤波器更高的保留了边缘效果,理论上来讲,图像中每点的分布都不为零,这也就是说每个像素的计算都需要包含整幅图像,但在实际应用中,在计算高斯函数的离散近似时,在大概3*sigma距离之外的像素都可以看作不起作用,这些像素的计算也就可以忽略不计,通常,图像处理只需要计算(6*sigma+1)*(6*sigma+1)的矩阵就可以保证相关像素影响。
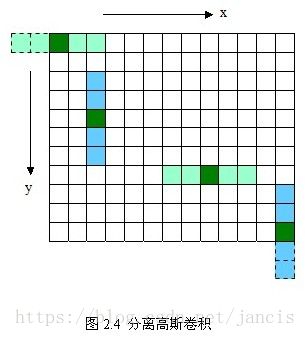
但二维矩阵模板会造成边缘图像缺失且随着sigma的变大,高斯模板和卷积运算量将大大增加,所以将高斯函数分离,使用二维矩阵变换得到的效果可以通过在水平方向进行一维高斯矩阵变换加上竖直方向的一维高斯矩阵变换得到,对用模板矩阵超出边界的部分——虚线框,将不做卷积计算。如图2.4中x方向的第一个模板1*5,将退化成1*3的模板,只在图像之内的部分做卷积。
对数学公式中高斯卷积方差sigma的选择:
先要理解几个概念:
高斯金字塔的模糊尺度:这个尺度是我们产生模板的尺度
摄像头模糊的尺度:这个尺度是图像被相机镜头模糊后的尺度,一般为固定值,这里定义0.5
图像的尺度:这个尺度是摄像头模糊尺度和高斯金字塔尺度的合作用,满足方和根的关系(对同一张图片进行连续多次高斯模糊与只用一次大的高斯模糊,可以达到一样的效果,如两次的模糊值分别为3和4,达到的效果可以只用5就可以)。Lowe定义图片的尺度为1.6
所以通过计算得到对第1组第1层进行高斯模糊的初始sigma为:
但别忘了前面对原始图像进行了扩大一倍的处理,所以真正对第1组第1层进行高斯模糊的初始sigma为:
将sigma1.25乘以一个比例系数k,得到一个新的平滑因子,用它来平滑第1组第2层的图像,结果图像作为第3层。如此这般重复,最后得到L层图像,在每一组中,每一层的尺寸都是一样的,只是平滑系数不一样。将第一组倒数第三层图像只作比例因子为2的降采样,其他不处理(指不进行高斯模糊)作为第2组的第1层(这样做的原因:为了保持在极值检测过程中高斯差分金字塔尺度空间的连续性,即高斯模糊系数的连续性),然后对第2组的第1层中的平滑因子通过乘以一个比例系数k,得到一个新的平滑因子,用它来平滑第2组第1层的图像,结果图像作为第2组的第2层,如此重复得到第2组的L层图像,同组内它们的尺寸是一样的,但是在尺寸方面第2组是第1组图像的一半。这样反复执行,就可以得到一共O组,每组L层,共计O*L个图像,这些图像一起构成高斯金字塔。
高斯差分金字塔是在高斯金字塔的基础上构建起来的,生成高斯金字塔的目的是为了构建高斯差分金字塔。高斯差分金字塔的第1组第1层是由高斯金字塔的第1组第2层减第1组第1层得到的,以此类推,逐组逐层生成每一个差分图像,所有差分图像构成差分金字塔,每一组在层数上,高斯差分金字塔比高斯金字塔少一层。
下图是对高斯金字塔和高斯差分金字塔的一个示意图,从图中也可以看出为了在检测极值过程中能够在每组图像中检测S(S表示层数,一般取3)个尺度的极值点,即满足尺度变化的连续性,将第一组倒数第三层图像作为第2组的第1层,且层数一般取3层,但要在3层的基础上再加3层变成6层才能满足要求。
小结:
高斯金字塔构建过程中的4个关键点:
(2)金字塔层数的确定,一般6层(不包括扩大一倍后的原图像)
(3)每一层尺度的确定
(4)下一组的图片降采样母本的确定
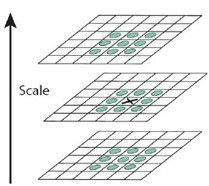
二、尺度空间中候选极值点的检测
SIFT特征点是由高斯差分空间的局部极值点经过筛选组成的,中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个点共26个点比较, 一个点如果在DOG尺度空间本层以及上下两层的26个领域中是最大或最小值时,就认为该点是图像在该尺度下一个候选的特征点,DoG图像中的大值和小值出现在图像区域发生较大变化的边缘处,没有变化的区域响应则接近于0,
三、对上一过程中得出的候选极值点进行筛选,去除低对比度的点和不稳定的边缘响应点,得到真正的特征点
1、去除低对比度的点
在SIFT中,图像局部块的对比度是用DOG响应的绝对值大小来度量的,因为DOG运算的本质是度量一个像素点和其周围像素的不同,值越大则对比度越高。去除小的值的点,保留有较大响应的点。SIFT通过构建尺度空间来计算不同尺度下观察到的特别的局部图像块,由于尺度采样操作的存在,上面找到的近似极值点落在像素点的位置上,而实际上如果在像素点附近用空间曲面去拟合的话,很多情况下极值点都不是恰好在像素点上,而是在附近,即极值点的位置存在偏移,为了得到更精确的极值点的位置和其响应值,SIFT中,假定了DOG响应局部区域的连续性,用二阶泰勒展开式来拟合并估计DOG的响应值,若该特征点的响应值的绝对值>=0.03,则保留该特征点,否则视为低对比度的点丢弃。
2、去除不稳定的边缘响应点
边缘的梯度值是朝同一个方向的,于是会呈现明显的梯度主方向,SIFT寻找的局部图像块,期望局部块中的主梯度方向与其他方向的梯度相差不要太大,通过计算DOG的二阶导数(Hessian矩阵),得到主梯度方向和其他方向的比值,保留该比值小于一定数值的局部特征点。去除仅落在边缘上而非角点的点,这类应被舍去的点有一个特征:沿着边缘切线方向的图像函数平缓(曲率小)。垂直边缘方向陡峭(曲率大)。由于Hessian矩阵的两个特征值是X,Y方向的曲率,所以求出每个极值点两个特征值的比例,设定一个界限,舍去不合格的点即可。
利用Hessian矩阵去除不稳定的边缘响应点的算法如下:
(1)对每个候选的极值点计算图像在X方向和Y方向的二阶偏导数以及图像XY方向的导数;
(2)根据第一步的结果,得到该候选极值点的Hessian矩阵:
Ixx表示X方向的二阶偏导数;Iyy表示Y方向的二阶偏导数;Ixy表XY方向的二阶导数
(3)求出该Hessian矩阵的两个特征值,那么矩阵的两个特征值之和就是矩阵的迹,两个特征值之积就是矩阵的行列式;
(4)将矩阵迹的平方与矩阵行列式的平方之比作为判断条件(这里假设两个特征值成比例关系,不一定是整数比例进行计算),若该“比”小于一定的阈值(阈值一般取10),则是真正的极值点。
四、特征点方向分配
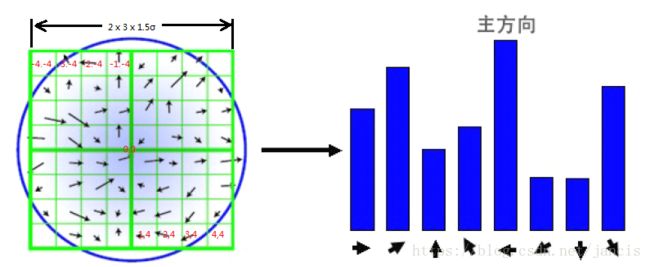
对上面的每个特征点,围绕该点选择一个窗口(圆形区域,以该特征点为中心,半径为3*sigma作一个圆域),窗口内各采样点的梯度方向构成一个直方图,根据直方图的峰值确定特征点的主方向, 直方图的峰值确定以后,任何大于峰值80%的方向(柱)创建一个具有该方向的特征点,这个方向认为是特征点的辅方向,因此,对于多峰值的情况,在同一位置和尺度就会产生多个具有不同方向的关键点,就是将该特征点复制成多份特征点(除了方向θ不同外,x,y,σ都相同)。 注意:特征点的尺度用来选择哪个高斯滤波图像参与计算,还用来决定窗口的大小(为了保证不同尺度下的同一特征点都包含相同的信息量,那么窗口的大小必须不一样:同一个原始图像,尺度越大,窗口应该越大;反之,如果窗口大小不变,尺度越大的图像包含的信息量越少。
窗口内各采样点的梯度方向和梯度幅值计算公式如下:
L为特征点所在的尺度空间值,大牛们计算模值是通过对高斯函数的sigma取1.5sigma的高斯分布加成的,高斯函数如下:
按尺度采样的3*sigma原则,邻域窗口半径为3*1.5sigma,分配给特征点的方向并不直接是特征点的梯度方向,且梯度幅值也不是直接累加到直方图中去的,每个累加到梯度方向直方图的采样点的幅值都要进行权重处理,加权采用圆形高斯加权函数,对于已经检测到的特征点,我们知道该特征点的尺度值sigma,因此根据这一尺度值,得到高斯函数方差为该特征点尺度sigma的1.5倍,形式为:
其中(i,j)为该点距离特征点的相对位置,左上角点像素距离特征点(0,0)(即中心点)的相对位置坐标为(-4,-4),同理,右下角像素为(4,4)。遍历邻域(绿色)中每个点,判断其梯度方向,将其加入相应的梯度方向直方图中,加入量为其梯度幅值 * wi,j ,例如左上角(-4,-4)的点,其梯度为方向为25°,梯度幅值为m,我们将其加入到hist[2]中(假设hist[0]为0°~10°的直方柱,hist[1]为10°~20°的直方柱,以此类推至hist[35]为350°~360°),加入的量为m* w(-4,-4),即hist[2] = hist[2] + mag* w(-4,-4)。直至遍历整个邻域,统计出该特征点出的梯度方向直方图。
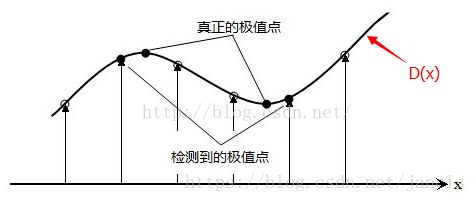
从上面可以看到做一个梯度方向的直方图,梯度方向直方图的横轴是梯度方向角,纵轴是梯度方向角对应的(带高斯权重)梯度幅值累加值,范围是0~360度,其中每10度一个柱,总共36个柱。直方图的一个柱表示一个角度范围,如10°~20°,这样得到的主方向或者辅方向是一个角度区间,需要进行抛物线插值来求出主方向和辅方向的角度,这样计算出来的主方向或者辅方向才是一个值。
抛物线插值的方法如下(i属于【0,35】):
由于角度是循环的,即0度=360度,如果出现h(j)超出了(0,……,35)的范围,那么可以通过圆周循环的方法找到它所对应的在0度到360度之间的值。如h(-1)=h(35)。
得到特征点的主方向后,对于每个特征点可以得到三个信息(x,y,σ,θ),即位置、尺度和方向。由此可以确定一个SIFT特征区域,一个SIFT特征区域由三个值表示,中心表示特征点位置,半径表示关键点的尺度,箭头表示主方向。具有多个方向的关键点可以被复制成多份,然后将方向值分别赋给复制后的特征点,一个特征点就产生了多个坐标、尺度相等,但是方向不同的特征点。为了确保旋转不变性,将图像旋转至特征点主方向与X轴方向重合。
五、特征点描述
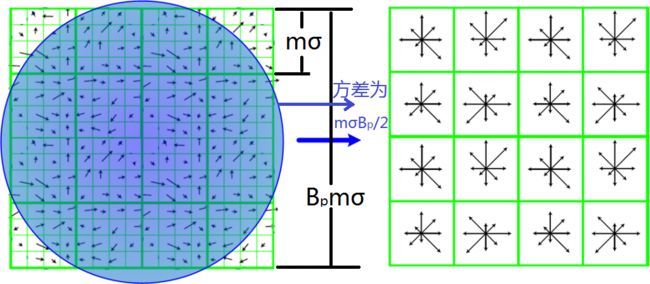
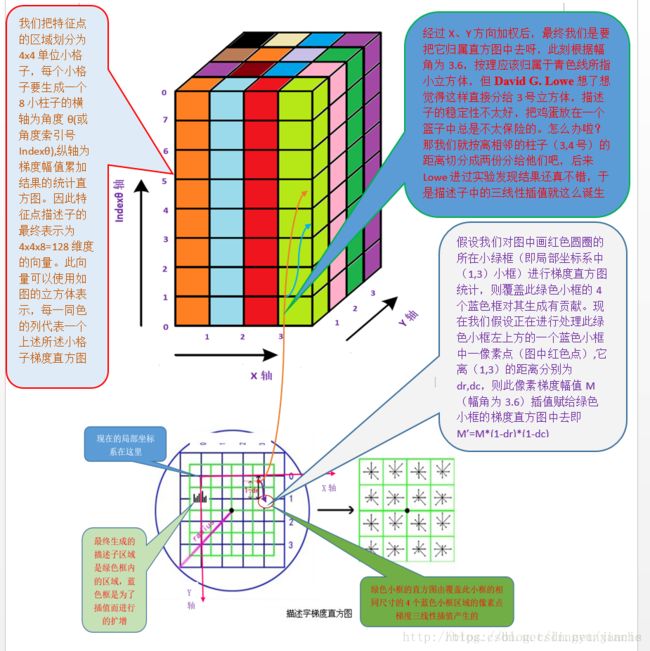
首先需要确定计算特征描述符的邻域范围,将特征点附近的邻域划分成4*4个子区域,每个子区域作为一个种子点,每个种子点有8个方向,这里与求特征点主方向时有所不同,此时每个子区域的梯度方向直方图将0度到360度划分为8个方向范围,每个范围为45度,这样每个种子点共有8个方向的梯度强度信息。
理论上来说,每个子区域的矩形边长为3*sigma,即一个子区域中包含(3*sigma)*(3*sigma)个像素,16个子区域的像素个数为4*4*(3*sigma)*(3*sigma)。但在实际中,由于如果邻域中像素的梯度方向为33度时,不能直接把它当作30度进行处理,应该要把它按照相邻的梯度方向30度到40度的距离切分成两份分给它们,所以就需要进行三线性插值的处理,所以将描述该特征点的窗口边长从3*sigma*d扩增至3*sigma*(d+1),这样整个区域的像素数就变成了【3*sigma*(d+1)】*【3*sigma*(d+1)】,但由于图像要旋转,所以整个区域的像素数又变成了【3*sigma*(d+1)*根号2】*【3*sigma*(d+1)*根号2】。虽然现在窗口的边长变成了3*sigma*(d+1),但最后用来描述特征点的区域边长还是3*sigma*d,所以实际得到的16个子区域的描述是通过窗口边长为3*sigma*(d+1)的区域经过计算得到的,即下图第二张图中绿色区域是由外面的蓝色区域计算得到,一个绿色区域由包含它的外面4个蓝色区域计算得到,至于具体怎么计算,见如下第二张图和第三张图。
下面两张图中的绿色区域就是用来描述特征点的16个邻域:
如上统计的4*4*8=128个梯度信息即为该特征点的特征向量。特征向量形成后,为了去除光照变化的影响,需要对它们进行归一化处理,公式如下:
当两幅图像的SIFT特征向量生成后,下一步采用特征点向量的欧式距离作为两幅图像中的特征点相似性判定度量,取图像1中的某个特征点,找出图像2中与其欧式距离最近的前两个特征点,在这两个特征点中,如果最近的距离与次近的距离比值小于某个阈值,则接受这一对匹配点,降低这个比例阈值,SIFT匹配点数量会减少,但更加稳定。