算法导论实验——递归与分治
大家如果对算法导论以及其他信息感兴趣,可以加入学习交流群一起交流 948097478
实验内容:
1.复习递归与分治的基本知识,了解分治的基本思想;
2.利用分治思想设计并解决常见问题,如矩阵相乘,循环赛日程表等
操作环境:
操作系统:Win XP/Win 7/Win8 操作系统
编程语言:C 语言
开发工具:e.g.,Microsoft Visual C++ 6.0
1 递归与分治算法设计与实现
问题描述:将正整数 n 表示成一系列正整数之和:n=n1+n2+…+nk,其中 n1≥n2 ≥…≥nk≥1,k≥1。正整数 n 的这种表示称为正整数 n 的划分。求正整数 n 的不同划分个数。列出算法设计过程,写出实现代码。
实现代码:
#include
#include
using namespace std;
//m为小于Number的正整数,NumDivide函数计算正整数m的划分中加数小于或等于m的所有划分
int NumDivide(int Number, int m){
if (Number < 1 || m < 1) return 0;
else if (Number == 1 || m == 1) return 1;
else if (Number < m) return NumDivide(Number, Number);
else if (Number == m) return NumDivide(Number, Number - 1) + 1;
else return NumDivide(Number, m - 1) + NumDivide(Number - m, m);
}
int main(void){
int Number,m,DivideTimes;
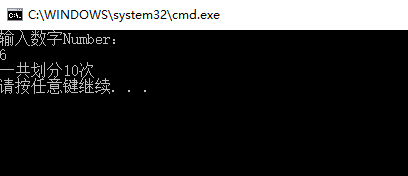
cout << "输入数字Number:" << endl;
cin >> Number;
DivideTimes = NumDivide(Number, Number - 1);
cout << "一共划分" << DivideTimes << "次" << endl;
return 0;
}
2.Strassen 矩阵乘法的 C 语言实现
问题描述: 求解两个矩阵 A 和 B 的乘积,C=AB,可将矩阵分块
![]()
根据矩阵乘法,可知矩阵 C 的计算公式:
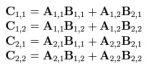
以上过程有 8 次乘法运算,4 次加法运算,矩阵乘法的复杂度主要就是体现在相乘上,而多一两次的加法并不会让复杂度上升太多。故此,是否可以让矩阵乘法的运算过程中乘法的运算次数减少?
现定义如下 7 个新矩阵:
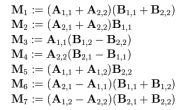
那么,矩阵 C 则可以通过以上 7 个矩阵计算得到
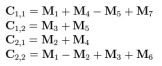
主要代码实现:
#include
#include
#include
#include
using namespace std;
template//函数模板声明
class Strassen_class {
public:
void ADD(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize);
void SUB(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize);
void MUL(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize);//朴素算法实现
void FillMatrix(T** MatrixA, T** MatrixB, int length);//A,B矩阵赋值
void PrintMatrix(T **MatrixA, int MatrixSize);//打印矩阵
void Strassen(int N, T **MatrixA, T **MatrixB, T **MatrixC);//Strassen算法实现
};
template
void Strassen_class::ADD(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize)
{
for (int i = 0; i < MatrixSize; i++)
{
for (int j = 0; j < MatrixSize; j++)
{
MatrixResult[i][j] = MatrixA[i][j] + MatrixB[i][j];
}
}
}
template
void Strassen_class::SUB(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize)
{
for (int i = 0; i < MatrixSize; i++)
{
for (int j = 0; j < MatrixSize; j++)
{
MatrixResult[i][j] = MatrixA[i][j] - MatrixB[i][j];
}
}
}
template
void Strassen_class::MUL(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize)
{
for (int i = 0; i
void Strassen_class::Strassen(int N, T **MatrixA, T **MatrixB, T **MatrixC)
{
int HalfSize = N / 2;
int newSize = N / 2;
if (N <= 32) //分治门槛,小于这个值时不再进行递归计算,而是采用常规矩阵计算方法
{
MUL(MatrixA, MatrixB, MatrixC, N);
}
else
{
T** A11;
T** A12;
T** A21;
T** A22;
T** B11;
T** B12;
T** B21;
T** B22;
T** C11;
T** C12;
T** C21;
T** C22;
T** M1;
T** M2;
T** M3;
T** M4;
T** M5;
T** M6;
T** M7;
T** AResult;
T** BResult;
//making a 1 diminsional pointer based array.
A11 = new T *[newSize];
A12 = new T *[newSize];
A21 = new T *[newSize];
A22 = new T *[newSize];
B11 = new T *[newSize];
B12 = new T *[newSize];
B21 = new T *[newSize];
B22 = new T *[newSize];
C11 = new T *[newSize];
C12 = new T *[newSize];
C21 = new T *[newSize];
C22 = new T *[newSize];
M1 = new T *[newSize];
M2 = new T *[newSize];
M3 = new T *[newSize];
M4 = new T *[newSize];
M5 = new T *[newSize];
M6 = new T *[newSize];
M7 = new T *[newSize];
AResult = new T *[newSize];
BResult = new T *[newSize];
int newLength = newSize;
//making that 1 diminsional pointer based array , a 2D pointer based array
for (int i = 0; i < newSize; i++)
{
A11[i] = new T[newLength];
A12[i] = new T[newLength];
A21[i] = new T[newLength];
A22[i] = new T[newLength];
B11[i] = new T[newLength];
B12[i] = new T[newLength];
B21[i] = new T[newLength];
B22[i] = new T[newLength];
C11[i] = new T[newLength];
C12[i] = new T[newLength];
C21[i] = new T[newLength];
C22[i] = new T[newLength];
M1[i] = new T[newLength];
M2[i] = new T[newLength];
M3[i] = new T[newLength];
M4[i] = new T[newLength];
M5[i] = new T[newLength];
M6[i] = new T[newLength];
M7[i] = new T[newLength];
AResult[i] = new T[newLength];
BResult[i] = new T[newLength];
}
//splitting input Matrixes, into 4 submatrices each.
for (int i = 0; i < N / 2; i++)
{
for (int j = 0; j < N / 2; j++)
{
A11[i][j] = MatrixA[i][j];
A12[i][j] = MatrixA[i][j + N / 2];
A21[i][j] = MatrixA[i + N / 2][j];
A22[i][j] = MatrixA[i + N / 2][j + N / 2];
B11[i][j] = MatrixB[i][j];
B12[i][j] = MatrixB[i][j + N / 2];
B21[i][j] = MatrixB[i + N / 2][j];
B22[i][j] = MatrixB[i + N / 2][j + N / 2];
}
}
//here we calculate M1..M7 matrices .
//M1[][]
ADD(A11, A22, AResult, HalfSize);
ADD(B11, B22, BResult, HalfSize); //p5=(a+d)*(e+h)
Strassen(HalfSize, AResult, BResult, M1); //now that we need to multiply this , we use the strassen itself .
//M2[][]
ADD(A21, A22, AResult, HalfSize); //M2=(A21+A22)B11 p3=(c+d)*e
Strassen(HalfSize, AResult, B11, M2); //Mul(AResult,B11,M2);
//M3[][]
SUB(B12, B22, BResult, HalfSize); //M3=A11(B12-B22) p1=a*(f-h)
Strassen(HalfSize, A11, BResult, M3); //Mul(A11,BResult,M3);
//M4[][]
SUB(B21, B11, BResult, HalfSize); //M4=A22(B21-B11) p4=d*(g-e)
Strassen(HalfSize, A22, BResult, M4); //Mul(A22,BResult,M4);
//M5[][]
ADD(A11, A12, AResult, HalfSize); //M5=(A11+A12)B22 p2=(a+b)*h
Strassen(HalfSize, AResult, B22, M5); //Mul(AResult,B22,M5);
//M6[][]
SUB(A21, A11, AResult, HalfSize);
ADD(B11, B12, BResult, HalfSize); //M6=(A21-A11)(B11+B12) p7=(c-a)(e+f)
Strassen(HalfSize, AResult, BResult, M6); //Mul(AResult,BResult,M6);
//M7[][]
SUB(A12, A22, AResult, HalfSize);
ADD(B21, B22, BResult, HalfSize); //M7=(A12-A22)(B21+B22) p6=(b-d)*(g+h)
Strassen(HalfSize, AResult, BResult, M7); //Mul(AResult,BResult,M7);
//C11 = M1 + M4 - M5 + M7;
ADD(M1, M4, AResult, HalfSize);
SUB(M7, M5, BResult, HalfSize);
ADD(AResult, BResult, C11, HalfSize);
//C12 = M3 + M5;
ADD(M3, M5, C12, HalfSize);
//C21 = M2 + M4;
ADD(M2, M4, C21, HalfSize);
//C22 = M1 + M3 - M2 + M6;
ADD(M1, M3, AResult, HalfSize);
SUB(M6, M2, BResult, HalfSize);
ADD(AResult, BResult, C22, HalfSize);
//at this point , we have calculated the c11..c22 matrices, and now we are going to
//put them together and make a unit matrix which would describe our resulting Matrix.
//组合小矩阵到一个大矩阵
for (int i = 0; i < N / 2; i++)
{
for (int j = 0; j < N / 2; j++)
{
MatrixC[i][j] = C11[i][j];
MatrixC[i][j + N / 2] = C12[i][j];
MatrixC[i + N / 2][j] = C21[i][j];
MatrixC[i + N / 2][j + N / 2] = C22[i][j];
}
}
// 释放矩阵内存空间
for (int i = 0; i < newLength; i++)
{
delete[] A11[i]; delete[] A12[i]; delete[] A21[i];
delete[] A22[i];
delete[] B11[i]; delete[] B12[i]; delete[] B21[i];
delete[] B22[i];
delete[] C11[i]; delete[] C12[i]; delete[] C21[i];
delete[] C22[i];
delete[] M1[i]; delete[] M2[i]; delete[] M3[i]; delete[] M4[i];
delete[] M5[i]; delete[] M6[i]; delete[] M7[i];
delete[] AResult[i]; delete[] BResult[i];
}
delete[] A11; delete[] A12; delete[] A21; delete[] A22;
delete[] B11; delete[] B12; delete[] B21; delete[] B22;
delete[] C11; delete[] C12; delete[] C21; delete[] C22;
delete[] M1; delete[] M2; delete[] M3; delete[] M4; delete[] M5;
delete[] M6; delete[] M7;
delete[] AResult;
delete[] BResult;
}//end of else
}
template
void Strassen_class::FillMatrix(T** MatrixA, T** MatrixB, int length)
{
cout << "输入A矩阵的值" << endl;
for (int row = 0; row> MatrixA[row][column];
//MatrixB[row][column] = (MatrixA[row][column] = rand() % 5);
//matrix2[row][column] = rand() % 2;//ba hazfe in khat 50% afzayeshe soorat khahim dasht
}
}
cout << "输入矩阵B的值" << endl;
for (int row = 0; row> MatrixB[row][column];
//MatrixB[row][column] = (MatrixA[row][column] = rand() % 5);
//matrix2[row][column] = rand() % 2;//ba hazfe in khat 50% afzayeshe soorat khahim dasht
}
}
}
template
void Strassen_class::PrintMatrix(T **MatrixA, int MatrixSize)
{
cout << endl;
for (int row = 0; row stra;//定义Strassen_class类对象
int MatrixSize = 0;
int** MatrixA; //存放矩阵A
int** MatrixB; //存放矩阵B
int** MatrixC; //存放结果矩阵
cout << "\n请输入矩阵大小(必须是2的幂指数值): ";
cin >> MatrixSize;
int N = MatrixSize;//for readiblity.
//申请内存
MatrixA = new int *[MatrixSize];
MatrixB = new int *[MatrixSize];
MatrixC = new int *[MatrixSize];
for (int i = 0; i < MatrixSize; i++)
{
MatrixA[i] = new int[MatrixSize];
MatrixB[i] = new int[MatrixSize];
MatrixC[i] = new int[MatrixSize];
}
stra.FillMatrix(MatrixA, MatrixB, MatrixSize); //矩阵赋值
//stra.MUL(MatrixA, MatrixB, MatrixC, MatrixSize);//朴素矩阵相乘算法 T(n) = O(n^3)
stra.Strassen(N, MatrixA, MatrixB, MatrixC); //strassen矩阵相乘算法
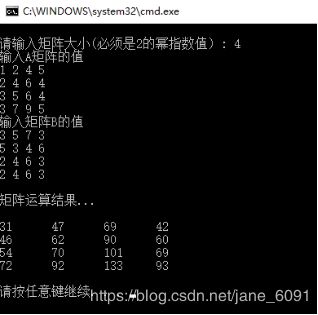
cout << "\n矩阵运算结果... \n";
stra.PrintMatrix(MatrixC, MatrixSize);//打印矩阵
system("Pause");
return 0;
}
结果分析与讨论:
当矩阵维数比较小(小于8时)使用简易算法,即直接进行矩阵相乘与相加所用时间比较短,效率高;当矩阵维数比较大(大于8)使用Strassen算法更加高效,时间复杂度低,运行速度快。
3.循环赛日程表问题问题描述:要求设计满足以下要求的比赛日程表
(1)每个选手必须与其他 n-1 个选手各赛一次;
(2)每个选手一天只能赛一次;
(3)循环赛一共进行 n-1 天。
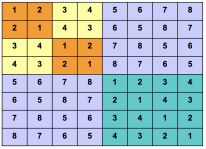
实现提示:
按分治策略,将所有的选手分为两半,n 个选手的比赛日程表就可以通过为 n/2 个选手设计的比赛日程表来决定。递归地用对选手进行分割,直到只剩下 2 个选手时,比赛日程表的制定就变得很简单。这时只要让这 2 个选手进行比赛就可以了。
程序源代码:
xunhuan.h
#include
#include
using namespace std;
void GameTable(vector > &vec);
void start();
xunhuan.cpp
#include "xunhuan.h"
void GameTable(vector > &vec){
if (vec.size() == 0){
return;
}
size_t s = vec.size();
int k = 0;
while (s = s >> 1){
//s = s >> 1;
k++;
}
//初始化
vec[0][0] = 1;
vec[0][1] = 2;
vec[1][0] = 2;
vec[1][1] = 1;
for (int i = 2; i <= k; i++){
int length = 0x1 << i;
int half = length >> 1;
//左下角的子表中项为左上角子表对应项加half=2^(i-1)
for (int row = 0; row < half; row++){
for (int col = 0; col < half; col++){
vec[row + half][col] = vec[row][col] + half;
}
}
//右上角的子表等于左下角子表
for (int row = 0; row < half; row++){
for (int col = 0; col < half; col++){
vec[row][col + half] = vec[row + half][col];
}
}
//右下角的子表等于左上角子表
for (int row = 0; row < half; row++){
for (int col = 0; col < half; col++){
vec[row + half][col + half] = vec[row][col];
}
}
}
}
void start(){
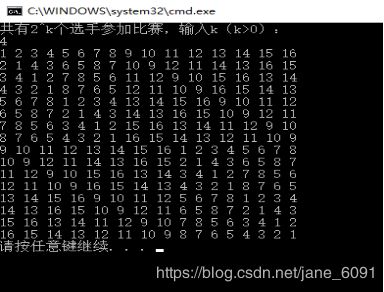
cout << "共有2^k个选手参加比赛,输入k(k>0):" << endl;
int k;
do{
cin >> k;
} while (k < 0 || k > 31);
int s = 0x1 << k;
vector > vec(s, vector(s, 0));
GameTable(vec);
for (size_t i = 0; i < vec.size(); i++){
for (size_t j = 0; j < vec[i].size(); j++){
cout << vec[i][j] << " ";
}
cout << endl;
}
}
main.cpp
#include "xunhuan.h"
int main(void){
start();
system("Pause");
return 0;
}
运行结果
有兴趣可以加群一起讨论:948097478