Ridge回归、Lasso回归、坐标下降法、最小角回归

Ridge回归

  可以看成是对最小二乘法的一种补充，岭回归通过对系数的大小施加惩罚来解决普通最小二乘法的一些问题。
它和一般线性回归的区别是在损失函数上增加了一个L2正则化的项，和一个调节线性回归项和正则化项权重的系数αα。损失函数表达式如下：

J(θ)=12(Xθ−Y)T(Xθ−Y)+12α||θ||22J(θ)=12(Xθ−Y)T(Xθ−Y)+12α||θ||22

其中 αα为常数系数，需要进行调优。 ||θ||2||θ||2为L2范数。
Ridge回归的解法和一般线性回归大同小异。如果采用梯度下降法，则每一轮 θθ迭代的表达式是：

θ=θ−(βXT(Xθ−Y)+αθ)θ=θ−(βXT(Xθ−Y)+αθ)

其中 ββ为步长。
如果用最小二乘法，则 θθ的结果是：

θ=(XTX+αE)−1XTYθ=(XTX+αE)−1XTY

其中E为单位矩阵。
  Ridge回归在不抛弃任何一个变量的情况下，缩小了回归系数，使得模型相对而言比较的稳定，但这会使得模型的变量特别多，模型解释性差。有没有折中一点的办法呢？即又可以防止过拟合，同时克服Ridge回归模型变量多的缺点呢？有，这就是下面说的Lasso回归。

Lasso回归

  Lasso回归有时也叫做线性回归的L1正则化，和Ridge回归的主要区别就是在正则化项，Ridge回归用的是L2正则化，而Lasso回归用的是L1正则化。Lasso回归的损失函数表达式如下:

J(θ)=12n(Xθ−Y)T(Xθ−Y)+α||θ||1J(θ)=12n(Xθ−Y)T(Xθ−Y)+α||θ||1

其中n为样本个数， αα为常数系数，需要进行调优。 ||θ||1||θ||1为L1范数。
  Lasso回归使得一些系数变小，甚至还是一些绝对值较小的系数直接变为0，因此特别适用于参数数目缩减与参数的选择，因而用来估计稀疏参数的线性模型。
  但是Lasso回归有一个很大的问题，导致我们需要把它单独拎出来讲，就是它的损失函数不是连续可导的，由于L1范数用的是绝对值之和，导致损失函数有不可导的点。也就是说，我们的最小二乘法，梯度下降法，牛顿法与拟牛顿法对它统统失效了。那我们怎么才能求有这个L1范数的损失函数极小值呢？

用坐标轴下降法求解Lasso回归

求解步骤：
  1.给定初始点(x1,x2,...,xnx1,x2,...,xn)
  2.固定除xixi意外其他维度的点，以xixi为自变量获取最小值
  3.换个维度，重复2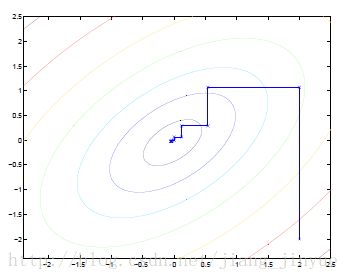

  可以看出，坐标下降法在每次迭代中在当前点处沿一个坐标方向进行一维搜索，固定其他的坐标方向，找到一个函数的局部极小值。
  坐标下降优化方法是一种非梯度优化算法。在整个过程中依次循环使用不同的坐标方向进行迭代，一个周期的一维搜索迭代过程相当于一个梯度迭代。
  gradient descent 方法是利用目标函数的导数（梯度）来确定搜索方向的，该梯度方向可能不与任何坐标轴平行。而coordinate descent方法是利用当前坐标方向进行搜索，不需要求目标函数的导数，只按照某一坐标方向进行搜索最小值,两者都是迭代方法，且每一轮迭代，都需要O(mn)的计算量(m为样本数，n为系数向量的维度)。

最小角回归法求解Lasso回归

1.前向选择（Forward Selection）算法

  问题是求解Y=XθY=Xθ中的θθ。其中YY为 mx1的向量，XX为mxn的矩阵，θθ为nx1的向量。m为样本数量，n为特征维度。
把矩阵XX看做n个mx1的向量XiXi(i=1,2,…n),在YY的XX变量XiXi(i =1,2,…m)中，选择和目标YY最为接近(余弦距离最大)的一个变量XkXk，用XkXk来逼近YY,得到下式：

Y¯¯¯¯=XkθkY¯=Xkθk

其中：

θk=Xk,Y||Xk||2θk=Xk,Y||Xk||2

即： Y¯¯¯¯Y¯,是 YY在 XkXk上的投影。那么,可以定义残差(residual): Yyes=Y−Y¯¯¯¯Yyes=Y−Y¯。由于是投影,所以很容易知道 Yyes和XkYyes和Xk是正交的。再以 YyesYyes为新的因变量，去掉 XkXk后,剩下的自变量的集合 XiXi{i=1,2,3…k−1,k+1,…n}为新的自变量集合,重复刚才投影和残差的操作，直到残差为0,或者所有的自变量都用完了,才停止算法。

  当 XX只有2维时，例子如上图，和 YY最接近的是 X1X1，首先在 X1X1上面投影，残差如上图长虚线。此时 X1θ1X1θ1模拟了 YY， θ1θ1模拟了 θθ(仅仅模拟了一个维度)。接着发现最接近的是 X2X2，此时用残差接着在 X2X2投影，残差如图中短虚线。由于没有其他自变量了，此时 X1θ1+X2θ2X1θ1+X2θ2模拟了 YY,对应的模拟了两个维度的 θθ即为最终结果，

2.前向梯度（Forward Stagewise）算法

  前向梯度算法和前向选择算法有类似的地方,不再使用投影的方式，而是在最接近的自变量XtXt的方向上移动一小步，在观察与残差YyesYyes最接近的自变量，直到残差足够小。

  当XX只有2维时，例子如上图，和YY最接近的是X1X1，首先在X1X1上面走一小段距离，此处εε为一个较小的常量，发现此时的残差还是和X1X1最接近。那么接着沿X1X1走，一直走到发现残差不是和X1X1最接近，而是和X2X2最接近，此时残差如上图长虚线。接着沿着X2X2走一小步，发现残差此时又和X1X1最接近，那么开始沿着X1X1走，走完一步后发现残差为0，那么算法停止。此时YY由刚才所有的所有步相加而模拟，对应的算出的系数θθ即为最终结果。
  当算法在ε很小的时候，可以很精确的给出最优解，当然，其计算的迭代次数也是大大的增加。和前向选择算法相比，前向梯度算法更加精确，但是更加复杂。有没有折中的办法可以综合前向梯度算法和前向选择算法的优点，做一个折中呢？有！这就是终于要出场的最小角回归法。

3.最小角回归(Least Angle Regression， LARS)算法

首先，依然是寻找到与因变量YY接近或者相关度最高的自变量XkXk,得到残差YyesYyes,不用与前向梯度一样一小步一小步的前进，直接走到出现一个XtXt的地方，使得XtXt和YyesYyes的相关度和XtXt与YyesYyes的相关度是一样的，此时残差YyesYyes就在XtXt和XkXk的角平分线上。沿着残差的角平分线走下去，直到出现下一个XpXp满足XpXp和YyesYyes的相关度和XtXt,XkXk与YyesYyes的相关度是一样的，直至YyesYyes足够小或者所有变量都取完。

当θ只有2维时，例子如上图，和Y最接近的是X1，首先在X1上面走一段距离，一直到残差在X1和X2的角平分线上，此时沿着角平分线走，直到残差最够小时停止，此时对应的系数β即为最终结果。
最小角回归法是一个适用于高维数据的回归算法，其主要的优点有：
1）特别适合于特征维度n 远高于样本数m的情况。
2）算法的最坏计算复杂度和最小二乘法类似，但是其计算速度几乎和前向选择算法一样
3）可以产生分段线性结果的完整路径，这在模型的交叉验证中极为有用
主要的缺点是：
由于LARS的迭代方向是根据目标的残差而定，所以该算法对样本的噪声极为敏感。