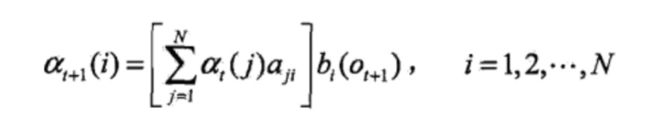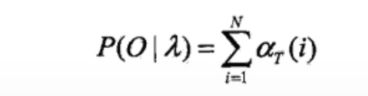- 机器学习中的贝叶斯网络:如何构建高效的风险预测模型
AI天才研究院
DeepSeekR1&大数据AI人工智能大模型自然语言处理人工智能语言模型编程实践开发语言架构设计
作者:禅与计算机程序设计艺术文章目录机器学习中的贝叶斯网络:如何构建高效的风险预测模型1.背景介绍2.基本概念术语说明2.1马尔科夫随机场(MarkovRandomField)2.2条件随机场(ConditionalRandomField,CRF)2.3变量elimination算法2.4贝叶斯网络3.核心算法原理和具体操作步骤以及数学公式讲解3.1原理介绍1.贝叶斯网络基础2.贝叶斯网络构建风险
- 使用 Milvus 进行向量数据库管理与实践
qahaj
milvus数据库python
技术背景介绍在当今的AI与机器学习应用中,处理和管理大量的嵌入向量是一个常见的需求。Milvus是一个开源向量数据库,专门用于存储、索引和管理深度神经网络以及其他机器学习模型生成的大规模嵌入向量。它的高性能和易用性使其成为处理向量数据的理想选择。核心原理解析Milvus的核心功能体现在其强大的向量索引和搜索能力。它支持多种索引算法,包括IVF、HNSW等,使其能够高效地进行大规模向量的相似性搜索操
- 物理学不存在了?诺贝尔物理学奖颁给了人工智能
资讯新鲜事
人工智能
2024年10月8日,瑞典皇家科学院宣布,将2024年诺贝尔物理学奖授予美国普林斯顿大学教授约翰·J·霍普菲尔德(JohnJ.Hopfield)和加拿大多伦多大学教授杰弗里·E·辛顿(GeoffreyE.Hinton),以表彰他们“在人工神经网络机器学习方面的基础性发现和发明”。辛顿在接受电话采访时表示:“完全没想到”。实话实说,在结果出来前,大家也都没想到。因为在外界预测里,今年的诺贝尔物理学奖
- PHP 爬虫实战:爬取淘宝商品详情数据
EcomDataMiner
php爬虫开发语言
随着互联网技术的发展,数据爬取越来越成为了数据分析、机器学习等领域的重要前置技能。而在这其中,爬虫技术更是不可或缺。php作为一门广泛使用的后端编程语言,其在爬虫领域同样也有着广泛应用和优势。本文将以爬取斗鱼直播数据为例,介绍php爬虫的实战应用。准备工作在开始爬虫之前,我们需要做一些准备工作。首先,需要搭建一个本地服务器环境,推荐使用WAMP、XAMPP等集成化工具,方便部署PHP环境。其次,我
- 强化学习中的深度卷积神经网络设计与应用实例
数字扫地僧
计算机视觉cnn人工智能神经网络
I.引言强化学习(ReinforcementLearning,RL)是机器学习的一个重要分支,通过与环境的交互来学习最优策略。深度学习,特别是深度卷积神经网络(DeepConvolutionalNeuralNetworks,DCNNs)的引入,为强化学习在处理高维度数据方面提供了强大工具。本文将探讨强化学习中深度卷积神经网络的设计原则及其在不同应用场景中的实例。II.深度卷积神经网络在强化学习中的
- 模拟退火算法:原理、应用与优化策略
尹清雅
算法
摘要模拟退火算法是一种基于物理退火过程的随机搜索算法,在解决复杂优化问题上表现出独特优势。本文详细阐述模拟退火算法的原理,深入分析其核心要素,通过案例展示在函数优化、旅行商问题中的应用,并探讨算法的优化策略与拓展方向,为解决复杂优化问题提供全面的理论与实践指导,助力该算法在多领域的高效应用与创新发展。一、引言在现代科学与工程领域,复杂优化问题无处不在,如资源分配、路径规划、机器学习模型参数调优等。
- TensorFlow深度学习实战项目:从入门到精通
点我头像干啥
Ai深度学习tensorflow人工智能
引言深度学习作为人工智能领域的一个重要分支,近年来取得了显著的进展。TensorFlow作为Google开源的深度学习框架,因其强大的功能和灵活的架构,成为了众多开发者和研究者的首选工具。本文将带领大家通过一个实战项目,深入理解TensorFlow的使用方法,并掌握深度学习的基本流程。1.TensorFlow简介1.1TensorFlow是什么?TensorFlow是一个开源的机器学习框架,由Go
- 国外7个最佳大语言模型 (LLM) API推荐
幂简集成
API新理念语言模型人工智能自然语言处理
大型语言模型(LLM)API将彻底改变我们处理语言的方式。在深度学习和机器学习算法的支持下,LLMAPI提供了前所未有的自然语言理解能力。通过利用这些新的API,开发人员现在可以创建能够以前所未有的方式理解和响应书面文本的应用程序。下面,我们将比较从Bard到ChatGPT、PaLM等市场上顶级LLMAPI。我们还将探讨整合这些LLM的潜在用例,并考虑其对语言处理的影响。什么是大语言模型(LLM)
- 机器学习是怎么一步一步由神经网络发展到今天的Transformer架构的?
yuanpan
机器学习神经网络transformer
机器学习和神经网络的发展经历了一系列重要的架构和技术阶段。以下是更全面的总结,涵盖了从早期神经网络到卷积神经网络之前的架构演变:1.早期神经网络:感知机(Perceptron)时间:1950年代末至1960年代。背景:感知机由FrankRosenblatt提出,是第一个具有学习能力的神经网络模型。它由单层神经元组成,可以用于简单的二分类任务。特点:输入层和输出层之间直接连接,没有隐藏层。使用简单的
- 奇异值分解(SVD)
文弱_书生
乱七八糟神经网络人工智能
奇异值分解(SVD)介绍奇异值分解(SVD),这是最强大的矩阵分解技术之一。SVD广泛应用于机器学习、数据科学和其他计算领域,用于降维、降噪和矩阵近似等应用。与仅适用于方阵的特征分解不同,SVD可以应用于任何矩阵,使其成为一种多功能工具。在这里煮啵将分解SVD背后的理论,通过手动计算示例进行分析,并展示如何在Python中实现SVD。在本节结束时,您将清楚地了解SVD的强大功能及其在机器学习中的应
- yum install locate出现Error: Unable to find match: locate解决方案
爱编程的喵喵
Linux解决方案linuxlocateyum解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的知识进行总结与归纳,不仅形成深入且独到的理解,而且能够帮助新手快速入门。 本文主要介绍了yuminstalllocate出现
- 【人工智能机器学习基础篇】——深入详解无监督学习之降维:PCA与t-SNE的关键概念与核心原理
猿享天开
人工智能数学基础专讲人工智能机器学习无监督学习降维
深入详解无监督学习之降维:PCA与t-SNE的关键概念与核心原理在当今数据驱动的世界中,数据维度的增多带来了计算复杂性和存储挑战,同时也可能导致模型性能下降,这一现象被称为“维度诅咒”(CurseofDimensionality)。降维作为一种重要的特征提取和数据预处理技术,旨在通过减少数据的维度,保留其主要信息,从而简化数据处理过程,并提升模型的性能。本文将深入探讨两种广泛应用于无监督学习中的降
- Flink启动任务
swg321321
flink大数据
Flink以本地运行作为解读例如:第一章Python机器学习入门之pandas的使用提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档文章目录Flink前言StreamExecutionEnvironmentLocalExecutorMiniClusterStreamGraph二、使用步骤1.引入库2.读入数据总结前言提示:这里可以添加本文要记录的大概内容:例如:随着人工智能的不断发
- 计算机专业毕业设计题目推荐(新颖选题)本科计算机人工智能专业相关毕业设计选题大全✅
会写代码的羊
毕设选题课程设计人工智能毕业设计毕设题目毕业设计题目aiAI编程
文章目录前言最新毕设选题(建议收藏起来)本科计算机人工智能专业相关的毕业设计选题毕设作品推荐前言2025全新毕业设计项目博主介绍:✌全网粉丝10W+,CSDN全栈领域优质创作者,博客之星、掘金/华为云/阿里云等平台优质作者。技术范围:SpringBoot、Vue、SSM、HLMT、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、小程序、大数据、机器学习等设计与开发。主要内容:免费功能
- 【机器学习】建模流程
CH3_CH2_CHO
什么?!是机器学习!!机器学习人工智能线性回归逻辑回归
1、数据获取1.1来源数据获取是机器学习建模的第一步,常见的数据来源包括数据库、API、网络爬虫等。数据库是企业内部常见的数据存储方式,例如:MySQL、Oracle等关系型数据库,以及MongoDB等非关系型数据库,它们能够存储大量的结构化和非结构化数据API(应用程序编程接口)提供了从外部获取数据的便捷方式,例如:社交媒体平台的API可以获取用户发布的内容和互动信息网络爬虫则适用于从网页中提取
- 机器学习课堂4线性回归模型+特征缩放
木尘152132
机器学习线性回归python
一、实验2-2,线性回归模型,计算模型在训练数据集和测试数据集上的均方根误差代码:#2-2线性回归模型importpandasaspdimportnumpyasnpimportmatplotlib.pyplotasplt#参数设置iterations=3000#迭代次数learning_rate=0.0001#学习率m_train=3000#训练样本的数量flag_plot_lines=False
- 【机器学习】模型拟合
CH3_CH2_CHO
什么?!是机器学习!!机器学习人工智能欠拟合过拟合
1、欠拟合1.1现象欠拟合是机器学习和统计建模中的一种常见问题,表现为模型无法充分捕捉数据中的潜在规律和模式。无论是训练数据还是测试数据,模型的预测误差都居高不下。在实际应用中,欠拟合的模型往往显得过于简单和粗糙,无法对数据进行有效的拟合和描述。1.2原因模型过于简单是导致欠拟合的主要原因:例如,使用直线去拟合具有明显曲线趋势的数据,或者使用低阶多项式去拟合高阶的复杂函数关系。这种情况下,模型的表
- 基于Python的智能决策支持系统:实现智能化决策的关键要素
AI天才研究院
DeepSeekR1&大数据AI人工智能大模型自然语言处理人工智能语言模型编程实践开发语言架构设计
文章目录基于Python的智能决策支持系统:实现智能化决策的关键要素11.背景介绍2.核心概念与联系数据收集与预处理模型构建与训练决策规则生成与优化决策结果评估与反馈3.核心算法原理具体操作步骤数据挖掘算法机器学习算法优化算法4.数学模型和公式详细讲解举例说明线性回归模型最小二乘法5.项目实践:代码实例和详细解释说明6.实际应用场景金融领域医疗领域供应链管理智能制造7.工具和资源推荐编程语言和开发
- 下一代模型技术演进与场景应用突破
智能计算研究中心
其他
内容概要当前模型技术正经历多维度的范式跃迁,可解释性模型与自动化机器学习(AutoML)成为突破传统黑箱困境的核心路径。在底层架构层面,边缘计算与量子计算的融合重构了算力分配模式,联邦学习技术则为跨域数据协作提供了安全可信的解决方案。主流框架如TensorFlow和PyTorch持续迭代优化能力,通过动态参数压缩与自适应超参数调优策略,显著提升模型部署效率。应用层创新呈现垂直化特征,医疗诊断模型通
- TypeScript语言的计算机视觉
苏墨瀚
包罗万象golang开发语言后端
使用TypeScript进行计算机视觉:一个现代化的探索引言随着人工智能和机器学习的快速发展,计算机视觉(ComputerVision)成为了一个极具活力的研究领域。计算机视觉旨在使计算机能够“看”和“理解”数字图像或视频中的内容。近年来,TypeScript作为一种现代化的编程语言,因其类型安全和更好的开发体验,逐渐在前端和后端开发中得到了广泛应用。本文将探讨如何使用TypeScript进行计算
- 人工智能之数学基础:数学对人工智能技术发展的作用
每天五分钟玩转人工智能
机器学习深度学习之数学基础人工智能深度学习机器学习神经网络自然语言处理数学
本文重点数学是人工智能技术发展的基础,它提供了人工智能技术所需的数学理论和算法,包括概率论、统计学、线性代数、微积分、图论等等。本文将从以下几个方面探讨数学对人工智能技术发展的作用。概率论和统计学概率论和统计学是人工智能技术中最为重要的数学分支之一。概率论和统计学的应用范围非常广泛,包括机器学习、数据挖掘、自然语言处理、计算机视觉等领域。在人工智能技术中,概率论和统计学主要用于处理不确定性的问题,
- 人工智能之数学基础:线性子空间
每天五分钟玩转人工智能
机器学习深度学习之数学基础人工智能深度学习线性代数线性子空间线性空间
本文重点在前面的课程中,我们学习了线性空间,本文我们我们在此基础上学习线性子空间。在应用中,线性子空间的概念被广泛应用于信号处理、机器学习、图像处理等领域。子空间的性质子空间是线性空间的一部分,它需要满足下面的性质:设V是数域F上的线性空间,W是V的一个非空子集。如果W对于V中的加法运算和数乘运算也构成F上的一个线性空间,则称W为V的线性子空间(或称向量子空间)。具体来说,设V是一个线性空间,W是
- 详解离线安装Python库
爱编程的喵喵
Python基础课程python离线安装requirements
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的知识进行总结与归纳,不仅形成深入且独到的理解,而且能够帮助新手快速入门。 本文主要介绍了详解离线安装Python库,希望能对
- ESG证书:AI预测未来十年职场人的黄金入场券
ESG学习圈
pandaspythondjango
当ChatGPT开始撰写ESG报告,当机器学习模型精准预测企业碳排放轨迹,一场由AI驱动的ESG革命正在颠覆传统可持续发展领域。根据彭博新能源财经预测,到2030年全球ESG资产管理规模将突破50万亿美元,而AI技术将成为撬动这个万亿级市场的核心杠杆。一、AI透视下的ESG黄金时代在微软开发的AI模型ESG-NOW系统中,通过分析全球4300家上市公司近十年的环境数据,成功预测2025年新能源行业
- 【Dive Into Stable Diffusion v3.5】1:开源项目正式发布——深入探索SDv3.5模型全参/LoRA/RLHF训练
Donvink
大模型#AIGCstablediffusionAIGC人工智能机器学习深度学习
目录1引言2项目简介3快速上手3.1下载代码3.2环境配置3.3项目结构3.4下载模型与数据集3.5运行指令3.6核心参数说明3.6.1通用参数3.6.2优化器/学习率3.6.3数据相关4结语1引言在人工智能和机器学习领域,生成模型的应用越来越广泛。StableDiffusion作为其中的佼佼者,因其强大的图像生成能力而备受关注。今天,我的开源项目DiveIntoStableDiffusionv3
- 知识库在意图识别中扮演着**数据支撑**和**语义理解辅助**的双重角色
PersistDZ
大数据与AI人工智能
知识库在意图识别中扮演着数据支撑和语义理解辅助的双重角色,而训练智能客服的意图识别Agent需要结合知识库的结构化数据与机器学习技术。以下是详细解析:一、知识库在意图识别中的作用1.提供标注数据意图标签定义:知识库中存储了预先定义的意图分类体系(如“订单查询”“退换货”“投诉”等),为模型提供明确的训练目标。标注样本:知识库包含大量用户对话历史及其对应的意图标签,是训练监督学习模型的核心数据源。2
- 近期计算机领域的热点技术
0dayNu1L
云计算量子计算人工智能
随着科技的飞速发展,计算机领域的新技术、新趋势层出不穷。本文将探讨近期计算机领域的几个热点技术趋势,并对它们进行简要的分析和展望。一、人工智能与机器学习人工智能(AI)和机器学习(ML)是近年来计算机领域最为热门的话题之一。AI和ML技术已经广泛应用于图像识别、自然语言处理、智能推荐等领域,并取得了显著的成果。随着技术的不断进步,AI和ML将更深入地渗透到各个行业,为人类社会带来更多便利和效益。在
- 计算机专业毕业设计题目推荐(新颖选题)本科计算机科学专业相关毕业设计选题大全✅
会写代码的羊
毕设选题课程设计计算机网络毕设选题毕设系统毕设题目计算机科学专业
文章目录前言最新毕设选题(建议收藏起来)本科计算机科学专业相关的毕业设计选题毕设作品推荐前言2025全新毕业设计项目博主介绍:✌全网粉丝10W+,CSDN全栈领域优质创作者,博客之星、掘金/华为云/阿里云等平台优质作者。技术范围:SpringBoot、Vue、SSM、HLMT、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、小程序、大数据、机器学习等设计与开发。主要内容:免费功能设计
- Linux安装Anaconda和Jupyter
硬水果糖
人工智能Linuxlinuxjupyter运维
一、了解Anaconda和Jupyter引言:Anaconda是一个流行的开源数据科学平台,广泛用于数据分析、机器学习、人工智能等领域。它是一个集成了大量科学计算和数据科学工具的Python和R编程语言环境。Anaconda的主要目标是简化数据科学和机器学习的开发流程,提供一个易于安装和管理的环境。而预装了大量常用的Python和R库,这些库涵盖了数据科学的各个方面,包括:数据分析:Pandas、
- ChatGPT、DeepSeek、GIS与Python机器学习强强联合!地质灾害风险评估、易发性分析、信息化建库及灾后重建
WangYan2022
DeepSeekChatGPT地下水地质灾害DeepSeekChatGPTGIS灾后重建
在地质灾害频繁肆虐的当下,精准开展风险评价刻不容缓。如今,一门极具创新性的教程震撼登场,它将ChatGPT、DeepSeek等前沿技术与GIS、Python以及机器学习深度交融,为学员打造出前所未有的学习体验,助力大家在地质灾害风险评价领域强势突围,一路领先。前沿技术融合,铸就智能学习核心动力教程最闪耀的亮点之一,便是大胆引入了ChatGPT和DeepSeek技术。它们恰似无所不能的“数据魔法师”
- apache 安装linux windows
墙头上一根草
apacheinuxwindows
linux安装Apache 有两种方式一种是手动安装通过二进制的文件进行安装,另外一种就是通过yum 安装,此中安装方式,需要物理机联网。以下分别介绍两种的安装方式
通过二进制文件安装Apache需要的软件有apr,apr-util,pcre
1,安装 apr 下载地址:htt
- fill_parent、wrap_content和match_parent的区别
Cb123456
match_parentfill_parent
fill_parent、wrap_content和match_parent的区别:
1)fill_parent
设置一个构件的布局为fill_parent将强制性地使构件扩展,以填充布局单元内尽可能多的空间。这跟Windows控件的dockstyle属性大体一致。设置一个顶部布局或控件为fill_parent将强制性让它布满整个屏幕。
2) wrap_conte
- 网页自适应设计
天子之骄
htmlcss响应式设计页面自适应
网页自适应设计
网页对浏览器窗口的自适应支持变得越来越重要了。自适应响应设计更是异常火爆。再加上移动端的崛起,更是如日中天。以前为了适应不同屏幕分布率和浏览器窗口的扩大和缩小,需要设计几套css样式,用js脚本判断窗口大小,选择加载。结构臃肿,加载负担较大。现笔者经过一定时间的学习,有所心得,故分享于此,加强交流,共同进步。同时希望对大家有所
- [sql server] 分组取最大最小常用sql
一炮送你回车库
SQL Server
--分组取最大最小常用sql--测试环境if OBJECT_ID('tb') is not null drop table tb;gocreate table tb( col1 int, col2 int, Fcount int)insert into tbselect 11,20,1 union allselect 11,22,1 union allselect 1
- ImageIO写图片输出到硬盘
3213213333332132
javaimage
package awt;
import java.awt.Color;
import java.awt.Font;
import java.awt.Graphics;
import java.awt.image.BufferedImage;
import java.io.File;
import java.io.IOException;
import javax.imagei
- 自己的String动态数组
宝剑锋梅花香
java动态数组数组
数组还是好说,学过一两门编程语言的就知道,需要注意的是数组声明时需要把大小给它定下来,比如声明一个字符串类型的数组:String str[]=new String[10]; 但是问题就来了,每次都是大小确定的数组,我需要数组大小不固定随时变化怎么办呢? 动态数组就这样应运而生,龙哥给我们讲的是自己用代码写动态数组,并非用的ArrayList 看看字符
- pinyin4j工具类
darkranger
.net
pinyin4j工具类Java工具类 2010-04-24 00:47:00 阅读69 评论0 字号:大中小
引入pinyin4j-2.5.0.jar包:
pinyin4j是一个功能强悍的汉语拼音工具包,主要是从汉语获取各种格式和需求的拼音,功能强悍,下面看看如何使用pinyin4j。
本人以前用AscII编码提取工具,效果不理想,现在用pinyin4j简单实现了一个。功能还不是很完美,
- StarUML学习笔记----基本概念
aijuans
UML建模
介绍StarUML的基本概念,这些都是有效运用StarUML?所需要的。包括对模型、视图、图、项目、单元、方法、框架、模型块及其差异以及UML轮廓。
模型、视与图(Model, View and Diagram)
&
- Activiti最终总结
avords
Activiti id 工作流
1、流程定义ID:ProcessDefinitionId,当定义一个流程就会产生。
2、流程实例ID:ProcessInstanceId,当开始一个具体的流程时就会产生,也就是不同的流程实例ID可能有相同的流程定义ID。
3、TaskId,每一个userTask都会有一个Id这个是存在于流程实例上的。
4、TaskDefinitionKey和(ActivityImpl activityId
- 从省市区多重级联想到的,react和jquery的差别
bee1314
jqueryUIreact
在我们的前端项目里经常会用到级联的select,比如省市区这样。通常这种级联大多是动态的。比如先加载了省,点击省加载市,点击市加载区。然后数据通常ajax返回。如果没有数据则说明到了叶子节点。 针对这种场景,如果我们使用jquery来实现,要考虑很多的问题,数据部分,以及大量的dom操作。比如这个页面上显示了某个区,这时候我切换省,要把市重新初始化数据,然后区域的部分要从页面
- Eclipse快捷键大全
bijian1013
javaeclipse快捷键
Ctrl+1 快速修复(最经典的快捷键,就不用多说了)Ctrl+D: 删除当前行 Ctrl+Alt+↓ 复制当前行到下一行(复制增加)Ctrl+Alt+↑ 复制当前行到上一行(复制增加)Alt+↓ 当前行和下面一行交互位置(特别实用,可以省去先剪切,再粘贴了)Alt+↑ 当前行和上面一行交互位置(同上)Alt+← 前一个编辑的页面Alt+→ 下一个编辑的页面(当然是针对上面那条来说了)Alt+En
- js 笔记 函数
征客丶
JavaScript
一、函数的使用
1.1、定义函数变量
var vName = funcation(params){
}
1.2、函数的调用
函数变量的调用: vName(params);
函数定义时自发调用:(function(params){})(params);
1.3、函数中变量赋值
var a = 'a';
var ff
- 【Scala四】分析Spark源代码总结的Scala语法二
bit1129
scala
1. Some操作
在下面的代码中,使用了Some操作:if (self.partitioner == Some(partitioner)),那么Some(partitioner)表示什么含义?首先partitioner是方法combineByKey传入的变量,
Some的文档说明:
/** Class `Some[A]` represents existin
- java 匿名内部类
BlueSkator
java匿名内部类
组合优先于继承
Java的匿名类,就是提供了一个快捷方便的手段,令继承关系可以方便地变成组合关系
继承只有一个时候才能用,当你要求子类的实例可以替代父类实例的位置时才可以用继承。
在Java中内部类主要分为成员内部类、局部内部类、匿名内部类、静态内部类。
内部类不是很好理解,但说白了其实也就是一个类中还包含着另外一个类如同一个人是由大脑、肢体、器官等身体结果组成,而内部类相
- 盗版win装在MAC有害发热,苹果的东西不值得买,win应该不用
ljy325
游戏applewindowsXPOS
Mac mini 型号: MC270CH-A RMB:5,688
Apple 对windows的产品支持不好,有以下问题:
1.装完了xp,发现机身很热虽然没有运行任何程序!貌似显卡跑游戏发热一样,按照那样的发热量,那部机子损耗很大,使用寿命受到严重的影响!
2.反观安装了Mac os的展示机,发热量很小,运行了1天温度也没有那么高
&nbs
- 读《研磨设计模式》-代码笔记-生成器模式-Builder
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
/**
* 生成器模式的意图在于将一个复杂的构建与其表示相分离,使得同样的构建过程可以创建不同的表示(GoF)
* 个人理解:
* 构建一个复杂的对象,对于创建者(Builder)来说,一是要有数据来源(rawData),二是要返回构
- JIRA与SVN插件安装
chenyu19891124
SVNjira
JIRA安装好后提交代码并要显示在JIRA上,这得需要用SVN的插件才能看见开发人员提交的代码。
1.下载svn与jira插件安装包,解压后在安装包(atlassian-jira-subversion-plugin-0.10.1)
2.解压出来的包里下的lib文件夹下的jar拷贝到(C:\Program Files\Atlassian\JIRA 4.3.4\atlassian-jira\WEB
- 常用数学思想方法
comsci
工作
对于搞工程和技术的朋友来讲,在工作中常常遇到一些实际问题,而采用常规的思维方式无法很好的解决这些问题,那么这个时候我们就需要用数学语言和数学工具,而使用数学工具的前提却是用数学思想的方法来描述问题。。下面转帖几种常用的数学思想方法,仅供学习和参考
函数思想
把某一数学问题用函数表示出来,并且利用函数探究这个问题的一般规律。这是最基本、最常用的数学方法
- pl/sql集合类型
daizj
oracle集合typepl/sql
--集合类型
/*
单行单列的数据,使用标量变量
单行多列数据,使用记录
单列多行数据,使用集合(。。。)
*集合:类似于数组也就是。pl/sql集合类型包括索引表(pl/sql table)、嵌套表(Nested Table)、变长数组(VARRAY)等
*/
/*
--集合方法
&n
- [Ofbiz]ofbiz初用
dinguangx
电商ofbiz
从github下载最新的ofbiz(截止2015-7-13),从源码进行ofbiz的试用
1. 加载测试库
ofbiz内置derby,通过下面的命令初始化测试库
./ant load-demo (与load-seed有一些区别)
2. 启动内置tomcat
./ant start
或
./startofbiz.sh
或
java -jar ofbiz.jar
&
- 结构体中最后一个元素是长度为0的数组
dcj3sjt126com
cgcc
在Linux源代码中,有很多的结构体最后都定义了一个元素个数为0个的数组,如/usr/include/linux/if_pppox.h中有这样一个结构体: struct pppoe_tag { __u16 tag_type; __u16 tag_len; &n
- Linux cp 实现强行覆盖
dcj3sjt126com
linux
发现在Fedora 10 /ubutun 里面用cp -fr src dest,即使加了-f也是不能强行覆盖的,这时怎么回事的呢?一两个文件还好说,就输几个yes吧,但是要是n多文件怎么办,那还不输死人呢?下面提供三种解决办法。 方法一
我们输入alias命令,看看系统给cp起了一个什么别名。
[root@localhost ~]# aliasalias cp=’cp -i’a
- Memcached(一)、HelloWorld
frank1234
memcached
一、简介
高性能的架构离不开缓存,分布式缓存中的佼佼者当属memcached,它通过客户端将不同的key hash到不同的memcached服务器中,而获取的时候也到相同的服务器中获取,由于不需要做集群同步,也就省去了集群间同步的开销和延迟,所以它相对于ehcache等缓存来说能更好的支持分布式应用,具有更强的横向伸缩能力。
二、客户端
选择一个memcached客户端,我这里用的是memc
- Search in Rotated Sorted Array II
hcx2013
search
Follow up for "Search in Rotated Sorted Array":What if duplicates are allowed?
Would this affect the run-time complexity? How and why?
Write a function to determine if a given ta
- Spring4新特性——更好的Java泛型操作API
jinnianshilongnian
spring4generic type
Spring4新特性——泛型限定式依赖注入
Spring4新特性——核心容器的其他改进
Spring4新特性——Web开发的增强
Spring4新特性——集成Bean Validation 1.1(JSR-349)到SpringMVC
Spring4新特性——Groovy Bean定义DSL
Spring4新特性——更好的Java泛型操作API
Spring4新
- CentOS安装JDK
liuxingguome
centos
1、行卸载原来的:
[root@localhost opt]# rpm -qa | grep java
tzdata-java-2014g-1.el6.noarch
java-1.7.0-openjdk-1.7.0.65-2.5.1.2.el6_5.x86_64
java-1.6.0-openjdk-1.6.0.0-11.1.13.4.el6.x86_64
[root@localhost
- 二分搜索专题2-在有序二维数组中搜索一个元素
OpenMind
二维数组算法二分搜索
1,设二维数组p的每行每列都按照下标递增的顺序递增。
用数学语言描述如下:p满足
(1),对任意的x1,x2,y,如果x1<x2,则p(x1,y)<p(x2,y);
(2),对任意的x,y1,y2, 如果y1<y2,则p(x,y1)<p(x,y2);
2,问题:
给定满足1的数组p和一个整数k,求是否存在x0,y0使得p(x0,y0)=k?
3,算法分析:
(
- java 随机数 Math与Random
SaraWon
javaMathRandom
今天需要在程序中产生随机数,知道有两种方法可以使用,但是使用Math和Random的区别还不是特别清楚,看到一篇文章是关于的,觉得写的还挺不错的,原文地址是
http://www.oschina.net/question/157182_45274?sort=default&p=1#answers
产生1到10之间的随机数的两种实现方式:
//Math
Math.roun
- oracle创建表空间
tugn
oracle
create temporary tablespace TXSJ_TEMP
tempfile 'E:\Oracle\oradata\TXSJ_TEMP.dbf'
size 32m
autoextend on
next 32m maxsize 2048m
extent m
- 使用Java8实现自己的个性化搜索引擎
yangshangchuan
javasuperword搜索引擎java8全文检索
需要对249本软件著作实现句子级别全文检索,这些著作均为PDF文件,不使用现有的框架如lucene,自己实现的方法如下:
1、从PDF文件中提取文本,这里的重点是如何最大可能地还原文本。提取之后的文本,一个句子一行保存为文本文件。
2、将所有文本文件合并为一个单一的文本文件,这样,每一个句子就有一个唯一行号。
3、对每一行文本进行分词,建立倒排表,倒排表的格式为:词=包含该词的总行数N=行号