【DSA】数据结构-堆详解（以最大堆为例）

堆

【定义】
堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组对象。

【注意】

• 这里讲的堆是一种数据结构，不是内存模型中堆的概念。
• 这里的堆是一种逻辑结构。

【性质】

• 堆中任意节点的值总是不大于(不小于)其子节点的值；
• 堆总是一棵完全树。

【说明】

• 将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。
• 堆是非线性数据结构，相当于一维数组，有两个直接后继。

二叉堆

二叉堆是完全二叉树或者是近似完全二叉树，它分为两种：最大堆和最小堆。

完全二叉树：若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。如下图所示都是完全二叉树。

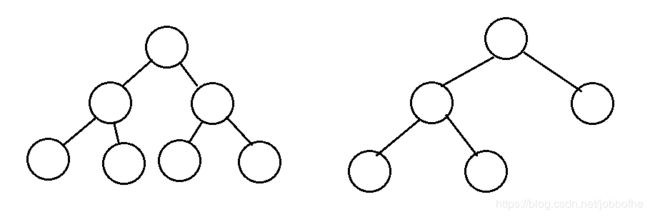
最大堆：父结点的键值总是大于或等于任何一个子节点的键值；
最小堆：父结点的键值总是小于或等于任何一个子节点的键值。
示意图如下：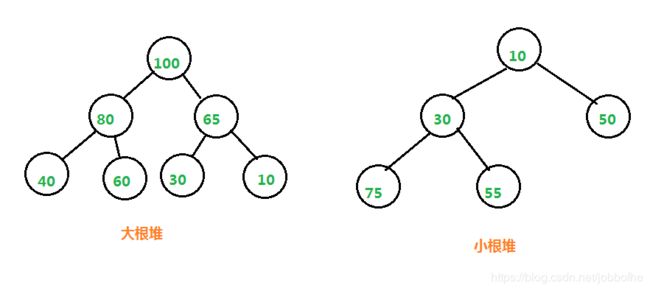

二叉堆实现

二叉堆一般都通过"数组"来实现。数组实现的二叉堆，父节点和子节点的位置存在一定的关系。有时候，我们将"二叉堆的第一个元素"放在数组索引0的位置，有时候放在1的位置。当然，它们的本质一样(都是二叉堆)，只是实现上稍微有一丁点区别。

【注意】本文二叉堆的实现统统都是采用"二叉堆第一个元素在数组索引为0"的方式！

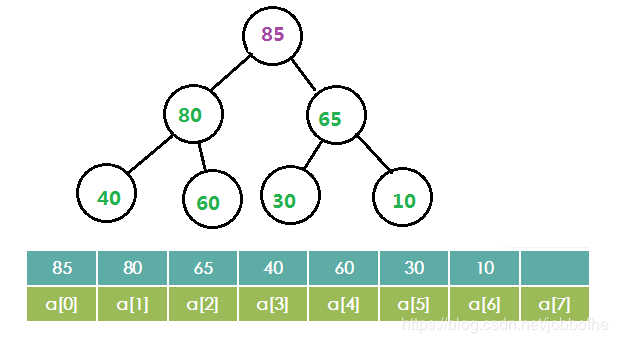
上图大根堆就有两种实现方式：

1. 第一个元素放在 索引 0 的位置
   此时，数组下表与节点的关系如下：

• 索引为 i 的左孩子的数组下标是 （2*i+1）
• 索引为 i 的右孩子的数组下标是 （2*i+2）
• 索引为 i 的父节点的数组下标是 （(i-1)/2）
  直观理解：
  当数组下标为0时，父节点就是a[0]，左孩子是a[1],右孩子是a[2]
  当数组下标为1时，父节点就是a[0]，左孩子是a[3],右孩子是a[4]
  当数组下标为2时，父节点就是a[0]，左孩子是a[5],右孩子是a[6]
  

2. 第一个元素放在 索引 1 的位置

• 索引为 i 的左孩子的数组下标是 （2*i）
• 索引为 i 的右孩子的数组下标是 （2*i+1）
• 索引为 i 的父节点的数组下标是 （2/2）
  这里不再赘述。
  

二叉堆的操作

二叉堆操作的方法的核心是【添加节点】、【删除节点】。以下示例均已大根堆为例。

添加节点示意图

插入节点85

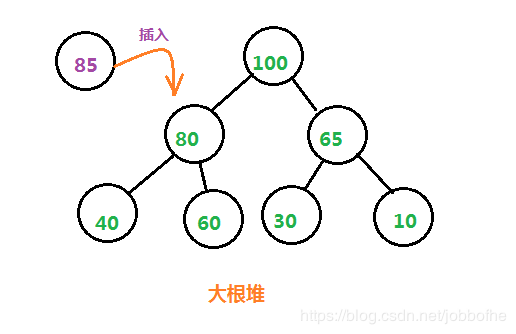
第一步：
将 新节点 插入数组的末尾。

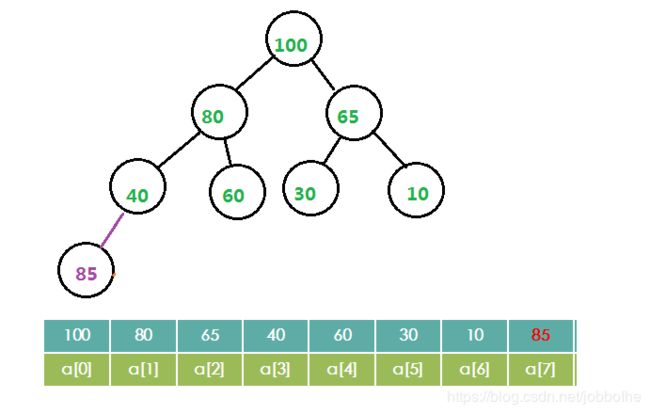
第二步：
比较新插入的节点和父节点的大小，这里 85 > 40, 则与父节点交换位置

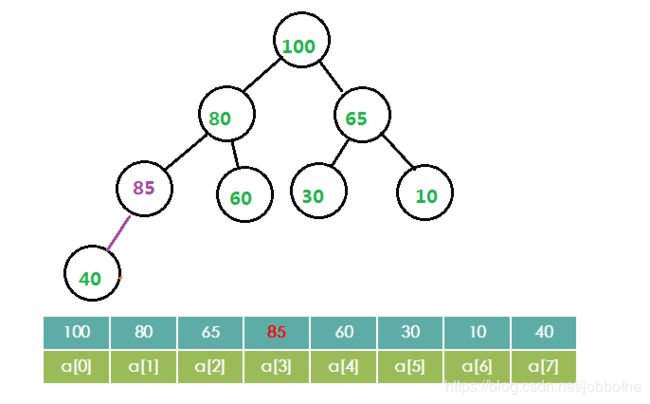
第三步：
重复上述比较步骤。

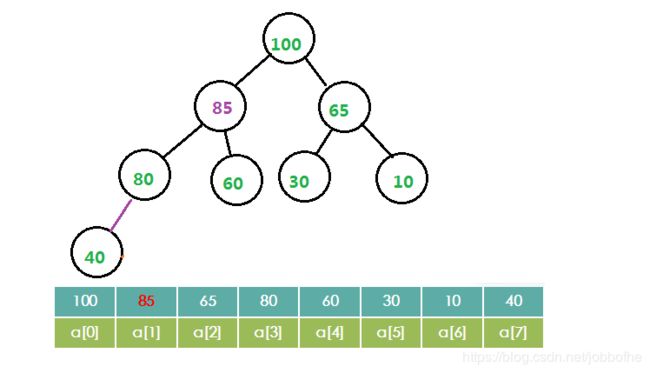
移动这步发现，85小于100，则停止移动。

删除节点示意图

以删除根节点为例
第一步：清除根节点的数据

第二步：将最末位的节点移到根节点

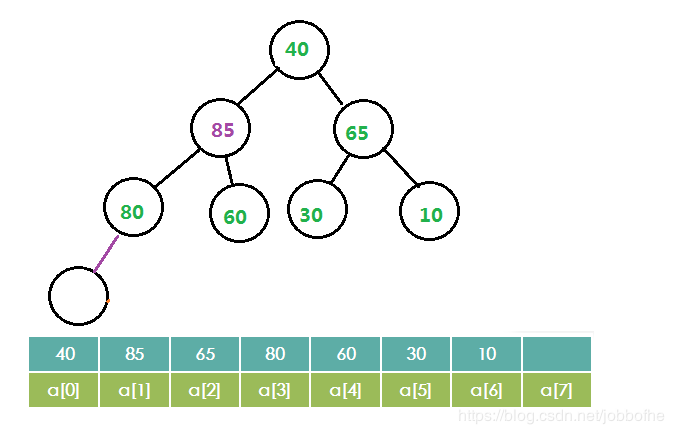
第三步：与两个子节点比较，选取较大的子节点与之交换

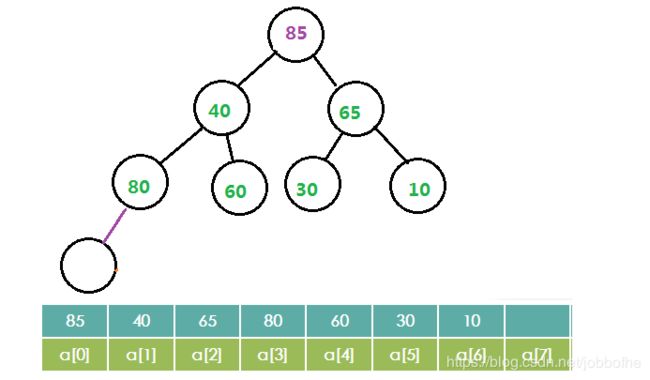
第四步：重复第三步

注意：如果删除的不是根节点，需要注意，删除完之后，还要保证替换后的树要是大根堆，并且是完全二叉树。

实现代码

#include 
#include 

#define ARRAY_LEN(arr) ((sizeof(arr))/sizeof(arr[0]))

#define MAX_NUM (128)

typedef int Type;

static Type heap_arr[MAX_NUM];
static int  heap_size = 0; // 堆数组的大小

/**
 * 根据数据 data 从对中获取对应的索引
 * @param  data [description]
 * @return      [description]
 */
int get_data_index_from_heap(int data)
{
    for (int i = 0; i < heap_size; ++i)
    {
        if (data == heap_arr[i])
        {
            return i;
        }
    }

    return -1;
}

/**
 * 在数组实现的堆中，向下调整元素的位置，使之符合大根堆
 * 注：   
 *     在数组试下你的堆中，第 i 个节点的
 *     左孩子的下标是 2*i+1， 
 *     右孩子的下标是 2*i+2,
 *     父节点的下标是 (i-1)/2
 *     
 * @param  start [一般从删除元素的位置开始]
 * @param  end   [数组的最后一个索引]
 */
static void max_heap_fixup_down(int start, int end)
{
    int curr_node_pos = start;
    int left_child = 2*start+1;
    int curr_node_data = heap_arr[curr_node_pos];



    while(left_child <= end) 
    {

        // left_child 是左孩子， left_child+1是同一个父节点下的右孩子
        if (left_child < end && heap_arr[left_child] < heap_arr[left_child+1])
        {
            // 从被删除的节点的左右孩子中选取较大的，赋值给父节点
            left_child++;
        }
        if (curr_node_data >= heap_arr[left_child])
        {
            // 选出孩子节点的较大者之后，与当前节点比较
            break;
        }
        else
        {
            heap_arr[curr_node_pos] = heap_arr[left_child];
            curr_node_pos = left_child;
            left_child = 2*left_child+1;
        }
    }

    heap_arr[curr_node_pos] = heap_arr[left_child];
}

/**
 * 删除对中的数据 data
 * @param data [description]
 */
static int max_heap_delete(int data)
{
    if (heap_size == 0)
    {
        printf("堆已空!\n");
        return -1;
    }
    int index = get_data_index_from_heap(data);
    if (index < 0)
    {
        printf("删除失败, 数据 [%d] 不存在!\n", data);
        return -1;
    }

    // 删除index的元素，使用最后的元素将其替换
    heap_arr[index] = heap_arr[--heap_size];

    // 删除元素之后，调整堆
    max_heap_fixup_down(index, heap_size-1);
}

/**
 * 在数组实现的堆中，将元素向上调整
 * 注：   
 *     在数组试下你的堆中，第 i 个节点的
 *     左孩子的下标是 2*i+1， 
 *     右孩子的下标是 2*i+2,
 *     父节点的下标是 (i-1)/2
 *     
 * @param  start [从数组的最后一个元素开始，start是最后一个元素的下标]
 */
static void max_heap_fixup_up(int start)
{
    int curr_node_pos = start;
    int parent = (start-1)/2;
    int curr_node_data = heap_arr[curr_node_pos];

    // 从最后一个元素开始比价，知道第0个元素
    while(curr_node_pos > 0) 
    {   
        // 当前节点的数据小于父节点，退出
        if (curr_node_data <= heap_arr[parent])
        {
            break;
        }
        else
        {
            // 交换父节点和当前节点
            heap_arr[curr_node_pos] = heap_arr[parent];
            heap_arr[parent] = curr_node_data;

            curr_node_pos = parent;
            parent = (parent-1)/2;
        }
    }
}

/**
 * 将新数据插入到二叉堆中
 * @param  data [插入数据]
 * @return      [成功返回0， 失败返回-1]
 */
int max_heap_insert(Type data)
{
    if (heap_size == MAX_NUM)
    {
        printf("堆已经满了！\n");
        return -1;
    }

    heap_arr[heap_size] = data;
    // 调整堆 
    max_heap_fixup_up(heap_size);
    heap_size++; // 对的数量自增

    return 0;
}

/**
 * 打印二叉堆
 */
void max_heap_print()
{
    for (int i = 0; i < heap_size; ++i)
    {
        printf("%d ", heap_arr[i]);
    }
}

int main(int argc, char const *argv[])
{
    Type tmp[] = {10, 40, 30, 60, 90, 70, 20, 50, 80};
    int len = ARRAY_LEN(tmp);

    printf("---> 添加元素：\n");
    for (int i = 0; i < len; ++i)
    {
        printf("%d ", tmp[i]);
        max_heap_insert(tmp[i]);
    }   

    printf("\n---> 最大堆: ");
    max_heap_print();

    max_heap_insert(85);
    printf("\n---> 插入元素之后 最大堆: ");
    max_heap_print();


    max_heap_delete(90);
    printf("\n---> 删除元素之后 最大堆: ");
    max_heap_print();
    printf("\n");

    return 0;
}

堆的应用场景

堆排序

分两个过程：建堆和排序，建堆的过程就是堆插入元素的过程，我们可以对初始数组原地建堆，然后再依次输出堆顶元素即可达到排序的目的。建堆的时间复杂度为 O(n)，排序过程的时间复杂度为 O(nlogn)，堆排序不是稳定的排序算法，因为在排序的过程中存在将堆的最后一个元素跟堆顶元素交换的操作，可能改变原始相对顺序。

堆常用来实现优先队列。

在队列中，操作系统调度程序反复提取队列中第一个作业并运行，因为实际情况中某些时间较短的任务将等待很长时间才能结束，或者某些不短小，但具有重要性的作业，同样应当具有优先权。堆即为解决此类问题设计的一种数据结构。
- 合并有序小文件

假如有 100 个小文件，每个小文件都为 100 MB，每个小文件中存储的都是有序的字符串，现在要求合并成一个有序的大文件，那么如何做呢？

直观的做法是分别取每个小文件的第一行放入数组，再比较大小，依次插入到大文件中，假如最小的行来自于文件 a，那么插入到大文件中后，从数组中删除该行，再取文件 a 的下一行插入到数组中，再次比较大小，取出最小的插入到大文件的第二行，依次类推，整个过程很像归并排序的合并函数。每次插入到大文件中都要循环遍历整个数组，这显然是低效的。

而借助于堆这种优先级队列就很高效。比如我们可以分别取 100 个文件的第一行建一个小顶堆，假如堆顶元素来自于文件 a，那么取出堆顶元素插入到大文件中，并从堆顶删除该元素（就是堆实现中 removeMax 函数）, 然后再从文件 a 中取下一行插入到堆顶中，重复以上过程就可以完成合并有序小文件的操作。

删除堆顶数据和往堆中插入数据的时间复杂度都是 O(logn)，n 表示堆中的数据个数，这里就是 100。

- 高性能定时器

假如有很多定时任务，如何设计一个高性能的定时器来执行这些定时任务呢？假如每过一个很小的单位时间（比如 1 秒），就扫描一遍任务，看是否有任务到达设定的执行时间。如果到达了，就拿出来执行。这显然是浪费资源的，因为这些任务的时间间隔可能长达数小时。

借助于堆这种优先级队列我们这可以这样设计：将定时任务按时间先后的顺序建一个小顶堆，先取出堆顶任务，查询其执行时间与当前时间之差，假如为 T 秒，那么在 T - 1 秒的时间内，定时器什么也不需要做，当 T 秒间隔达到时就取出任务执行，对应的从堆顶删除堆顶元素，然后再取下一个堆顶元素，查询其执行时间。

这样，定时器既不用间隔 1 秒就轮询一次，也不用遍历整个任务列表，性能也就提高了。

- topK 问题

取 top k 元素的情形可分为两类，一类是静态数据集合，也就是说数据确定后不再增加新的元素，另一类是动态数据集合，会随时增加元素，但依然求第 k 大元素。

对于静态数据，我们可以先从静态数据依次插入小顶堆中，维护一个大小为 k 的小顶堆，遍历其余数据，依次插入到大小为 k 的小顶堆中，如果元素比 k 小，则不做处理，继续遍历下一个数据，如果比 k 大，则删除堆顶堆，并将该值插入到堆顶中，这样遍历结束时，堆顶元素就是第 k 大元素。

遍历数组需要 O(n) 的时间复杂度，一次堆化操作需要 O(logK) 的时间复杂度，所以最坏情况下，n 个元素都入堆一次，所以时间复杂度就是 O(nlogK)。

对于动态数据，处理方法也是一样的，相当于实时求 top k，那么每次求 top k 时重新计算一下即可，时间复杂度仍是 O(nlogK)，n 表示当前的数据的大小。我们可以一直都维护一个 K 大小的小顶堆，当有数据被添加到集合中时，我们就拿它与堆顶的元素对比。如果比堆顶元素大，我们就把堆顶元素删除，并且将这个元素插入到堆中；如果比堆顶元素小，则不做处理。这样，无论任何时候需要查询当前的前 K 大数据，我们都可以里立刻返回给他。