最短路径-Floyd算法的matlab实现.md
最短路径-Floyd算法的matlab实现
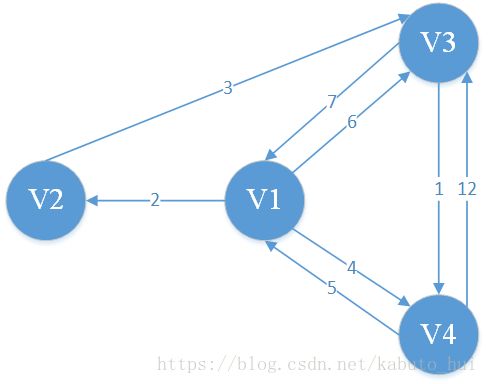
弗洛伊德算法是解决任意两点间的最短路径的一种算法,可以正确处理有向图或有向图或负权(但不可存在负权回路)的最短路径问题。
在Floyd算法中一般有两个矩阵,一个距离矩阵D,一个路由矩阵R,其中距离矩阵用于存储任意两点之间的最短距离,而路由矩阵则记录任意两点之间的最短路径信息。
其思想是:如果可以从一个点进行中转,就进行比较从这个点中转和不中转的距离,存储距离小的情况,并更新距离矩阵和路由矩阵。
从算法思想中我们可以大概推断我们要遍历n个中转点,在每个中转点进行操作的时候,需要对任意两点之间 的距离进行遍历。那么算法就应该有三重循环,第一重循环是遍历中转点,第二重和第三重循环是遍历任意两个点之间的距离。假设中转节点为K,那么节点i与j之间的最小距离怎么更新呢?
D ( i , K ) + D ( K , j ) < D ( i , j ) D(i,K)+D(K,j) < D(i,j) D(i,K)+D(K,j)<D(i,j)
其中D(i,K)+D(K,j)表示i到j从K中转的距离,D(i,j)表示从i到j的最短距离,如果前者比后者小,那么就D(i,j)进行更新: D ( i , j ) = D ( i , K ) + D ( K , j ) D(i,j) = D(i,K)+D(K,j) D(i,j)=D(i,K)+D(K,j),这样就更新了距离矩阵。怎么记录这条最短路径呢,这个时候就需要更新我们的路由矩阵: R ( i , j ) = R ( i , K ) R(i,j) = R(i,K) R(i,j)=R(i,K)
路由矩阵很好理解,比如最开始是R(4,3) = 3,表示V4到V3一步就可以到达V3,如果现在可以从V2中转到达,那么R(4,3) = R(4,2) =2,表示V4->V3要先经过V2才能到达。
这个时候我们可以写出距离矩阵D和路由矩阵R如下:
可以由V1中转,那么V1到到各个点的距离还是不变。V2没有到达V1的路径,所以也就不存在从V1中转的情况,所以V2到各个点的距离还是不变。
V3可以经由V1中转,那么这个时候判断一下中转前和中转后的距离大小,将最小距离留存下来如:
V3->V1 = 7 不变
V3->V2 = inf,经由V1中转之后V3->V1->V2 = 9, 于是V3到V2的最短距离变化为9,更新路由矩阵R(3,2) = R(3,1) = 1
V3->V4 = 1,经由V1中转之后V3->V1->V4 = 11, 于是V3到V4的最短距离就还是1
同理:
V4->V2 = inf, 经由V1中转之后V4->V1->V2 = 7, 于是V4到V2的最短距离变化为7,更新路由矩阵R(4,2) = R(4,1) = 1
V4->V3 = 12,经由V1中转之后V4->V1->V3 = 11, 于是V4到V2的最短距离变化为11,更新路由矩阵R(4,3) = R(4,1) = 1
那么距离矩阵和路由矩阵变化为:


现在假设在从V1中转的基础上,图中的每个点之间还可以经由V2中转,于是:
V1->V2 = 2
V1->V3 = 6,经由V2中转之后V1->V2->V3 = 5, 于是V1到V3的最短距离变化为5,更新路由矩阵R(1,3) = R(1,2) = 2
V1->V4 = 4
V2->V1 = inf
V2->V3 = 3
V2->V4 = inf
V3->V1 = 7
V3->V2 = 9
V3->V4 = 1
V4->V1 = 5
V4->V2 = 7
V4->V3 = 11,经由V2中转之后V4->V2->V3 = 10, 于是V4到V3的最短距离变化为10,更新路由矩阵R(4,3) = R(4,2) = 1。
于是现在的距离矩阵和路由矩阵可以变为:

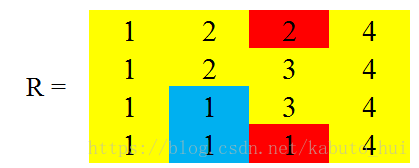
现在假设在从V1中转的基础上,图中的每个点之间还可以经由V3中转,于是:
V1->V2 = 2
V1->V3 = 5
V1->V4 = 4
V2->V1 = inf,经由V3中转之后V2->V3->V1 = 10, 于是V2到V1的最短距离变化为10,更新路由矩阵R(2,1) = R(2,3) = 3。
V2->V3 = 3
V2->V4 = inf,经由V3中转之后V2->V3->V4 = 4, 于是V2到V5的最短距离变化为4,更新路由矩阵R(2,4) = R(2,3) = 3。
V3->V1 = 7
V3->V2 = 9
V3->V4 = 1
V4->V1 = 5
V4->V2 = 7
V4->V3 = 10
于是现在的距离矩阵和路由矩阵可以变为:

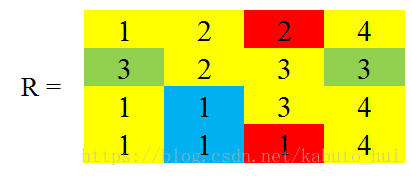
现在假设在从V1中转的基础上,图中的每个点之间还可以经由V4中转,于是:
V1->V2 = 2
V1->V3 = 5
V1->V4 = 4
V2->V1 = 10,经由V4中转之后V2->V4->V1 = 9, 于是V3到V1的最短距离变化为9,更新路由矩阵R(2,1) = R(2,4) = 3。
V2->V3 = 3
V2->V4 = 4
V3->V1 = 7,经由V4中转之后V3->V4->V1 = 6, 于是V3到V1的最短距离变化为6,更新路由矩阵R(3,1) = R(3,4) = 4。
V3->V2 = 9,经由V4中转之后V3->V4->V2 = 8, 于是V3到V1的最短距离变化为8,更新路由矩阵R(3,2) = R(3,4) = 4。
V3->V4 = 1
V4->V1 = 5
V4->V2 = 7
V4->V3 = 10
于是现在的距离矩阵和路由矩阵可以变为:


好了,到此所有点都中转过了,任意两点之间的最短距离就是最后距离矩阵中的数据,那么其路径该怎么表示呢?路径全部记录在路由矩阵中了,我们只要读取路由矩阵就可以了。
举个例子:v4->V3
从距离矩阵中可以看出V4->V3的最短距离是D(4,3) = 10;根据其路由矩阵我们可以看出:
R(4,3) = 1,表示V4->V3,先经过V1,于是再看R(1,3) = 2,表示还需要再经过V2,于是我们看R(2,3) = 3,这个时候我们发现终于到了V3,所以我们梳理一下,V4->V3的最短路径是:V4->V1->V2->V3。简言之就是固定列,根据路由矩阵在行中跳转,直到跳转到对应的点。
所以最后我们展示出代码就很容易理解了:
% floyd.m
% 采用floyd算法计算图a中每对顶点最短路
% d是矩离矩阵
% r是路由矩阵
function [d,r]=floyd(a)
n=size(a,1);
% 初始化距离矩阵
d=a;
% 初始化路由矩阵
for i=1:n
for j=1:n
r(i,j)=j;
end
end
r;
% Floyd算法开始
for k=1:n
for i=1:n
for j=1:n
if d(i,k)+d(k,j)最后我还写了一个用于打印路径的函数:
% DisplayPath.m 打印路径函数
function DisplayPath(route, start, dest)
% 打印出任意两点之间的最短路径
% route : 路由表
% start : 起点index
% dest : 终点index
i = 1;
while 1
if(route(start, dest) ~= dest)
fprintf('V%s -> ', num2str(start));
start = route(start, dest);
else
fprintf('V%s -> ', num2str(start));
fprintf('V%s\n', num2str(dest));
break;
end
end
我将上面的举例的图使用floyd算法进行计算,并最后打印出任意两点之间的最短路径:
a = [0 2 6 4;
inf 0 3 inf;
7 inf 0 1 ;
5 inf 12 0];
[d,r]=floyd(a)
disp('--------------------------')
for i = 1 : 4
for j = 1 : 4
DisplayPath(r, i, j);
end
end
运行结果为:
main
d =
0 2 5 4 9 0 3 4 6 8 0 1 5 7 10 0r =
1 2 2 4 3 2 3 3 4 4 3 4 1 1 1 4
V1 -> V1
V1 -> V2
V1 -> V2 -> V3
V1 -> V4
V2 -> V3 -> V4 -> V1
V2 -> V2
V2 -> V3
V2 -> V3 -> V4
V3 -> V4 -> V1
V3 -> V4 -> V1 -> V2
V3 -> V3
V3 -> V4
V4 -> V1
V4 -> V1 -> V2
V4 -> V1 -> V2 -> V3
V4 -> V4