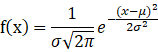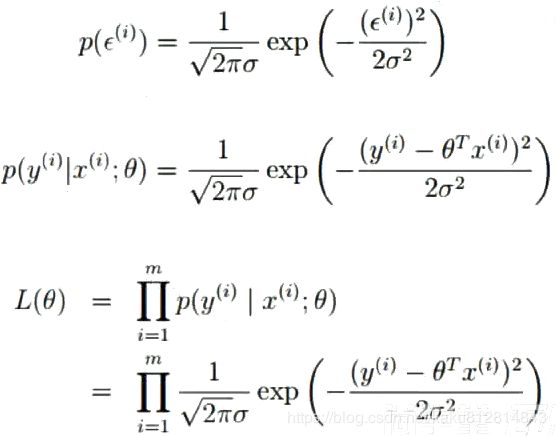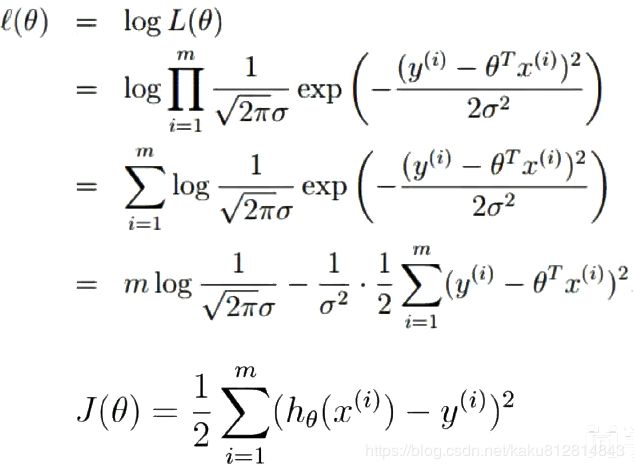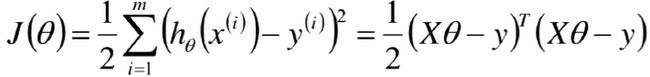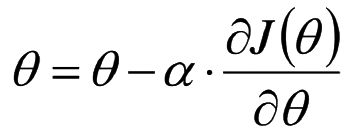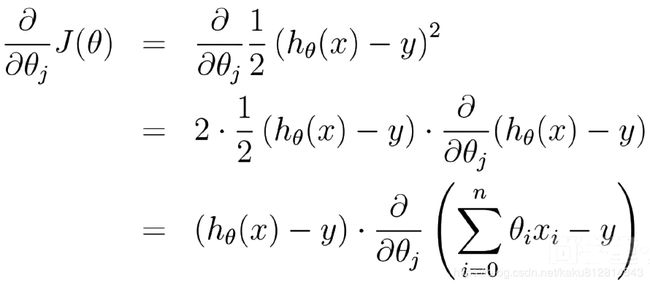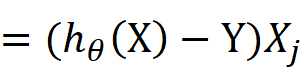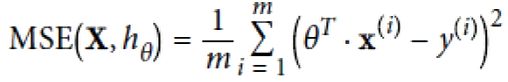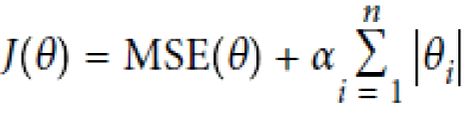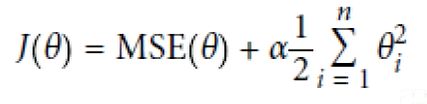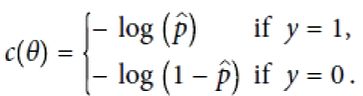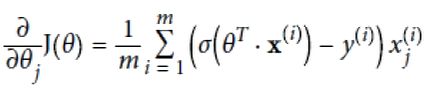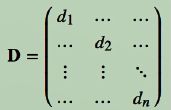机器学习笔记
机器学习(machine learning):用已有的数据训练某种模型,利用模型预测未来
Python机器学习库官网https://scikit-learn.org/stable/
机器学习分为有监督的机器学习和无监督的机器学习
有监督的机器学习:回归、分类
无监督的机器学习:聚类、降维
numpy数学计算框架
scipy物理计算框架
pandas数据分析框架
matplotlib绘图框架
scikit-learn机器学习框架
tensorflow谷歌开源的深度学习框架
keras开源的深度学习框架
回归平均值(regression to the mean),回归问题主要关注确定一个唯一的因变量(dependent variable)(需要预测的值)和一个或多个数值型的自变(independent variables)预测变量)之间的关系,广义线性回归,GLM,比如,逻辑回归,泊松回归
线性:y=a*x 一次方变化
回归:回归到平均值
线性回归(预测):一元一次方程组y=a*x+b,影响y的因素(维度)只有一个x即一元
多元线性回归:多元一次方程组y=w1*x1+w2*x2+…+wn*wn即y=W^T*X(权重矩阵W的转置矩阵点积矩阵X)
机器学习是以最快速度找到误差最小最优解(没有完美解)
使用最小二乘法求解样本误差的最小值即为函数模型最优解,样本模型的误差近似正态分布
根据最大似然估计(求样本集相关概率密度函数的参数)和中心极限定理(随机变量序列部分和分布近似正态分布)找到样本模型的误差最小最优解
使用概率密度乘积近似概率乘积的总似然即概率密度乘积最大相当于总似然最大
样本的误差的最小二乘法函数符合凹函数,求导后斜率即梯度为0时误差的和最小最优
θ=(XTX)-1XTY![]()
θ矩阵为样本函数模型最优解的参数矩阵即维度矩阵X的权重
正态分布的概率密度函数:
import numpy as np 引入numpy科学计算模块
import matplotlib.pyplot as plt 引入绘图模块
X=2*np.random.rand(100,1) numpy.random.rand()获取一个或一组服从“0~1”均匀分布的随机样本值
y=4+3*X+np.random.randn(100,1) numpy.random.randn()获取一个或一组服从“0~1”正态分布的随机样本值
X_b=np.c_[np.ones((100,1)),X] numpy.ones()获取给定形状和类型的新数组,numpy.c_[]获取切片对象转换为沿第二轴的连接
theta_best=np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y) numpy.dot()矩阵点积,numpy.linalg.inv()矩阵的逆
X_new=np.array([[0],[2]]) numpy.array()从常规Python列表或元组创建数组
X_new_b=np.c_[(np.ones((2,1))),X_new]
y_predict=X_new_b.dot(theta_best)
plt.plot(X_new,y_predict,"r-") matplotlib.pyplot.plot()绘制图形
plt.plot(X,y,"b.")
plt.axis([0,2,0,15]) matplotlib.pyplot.axis()设置轴属性
plt.show()
维度矩阵的点积复杂度是O(N)三次方
梯度下降法算法:以最快速度找到最优解的算法
梯度下降法一般流程为先初始化theta、求梯度斜率gradient、theta_t+1=theta_t-gradient*learning_rate(超参数learning_rate太大会振荡太小会时间长迭代次数多)、等迭代到gradient import numpy as np __author__ = '作者名' X = 2 * np.random.rand(100, 1) y = 4 + 3 * X + np.random.randn(100, 1) X_b = np.c_[np.ones((100, 1)), X] learning_rate = 0.1 学习率即步长 n_iterations = 10000 迭代次数 m = 100 样本数量 #初始化theta theta = np.random.randn(2, 1) count = 0 #一般不设置阈值设置超参数迭代次数,迭代一定次数后认为收敛 for iteration in range(n_iterations): count += 1 #求梯度gradient gradients = 1/m * X_b.T.dot(X_b.dot(theta)-y) #应用公式调整theta值,theta_t+1= theta_t-gradient*learning_rate theta = theta - learning_rate * gradients print(count) print(theta) 批量梯度下降:使用所有样本求梯度均值grads=(1/m)*X^Transpose*(X*theta-Y) 随机梯度下降:不使用所有样本随机抽取一个样本进行求梯度grad_j=(1/m)* (Xj)^Transpose*(X*theta-y),求梯度速度快但迭代次数多,可能找不到全局最优解 小批量梯度下降(Mini-Batch GD):不使用所有的样本数据而是随机选择一部分样本数据来求梯度 import numpy as np X = 2 * np.random.rand(100, 1) y = 4 + 3 * X + np.random.randn(100, 1) X_b = np.c_[np.ones((100, 1)), X] n_epochs=500 t0,t1=5,50 #超参数 m = 100 def learning_schedule(t): 随着迭代次数的增多,不断减小学习率步长 return t0/(t+t1) theta = np.random.randn(2, 1) for epoch in range(n_epochs): for i in range(m): random_index=np.random.randint(m) xi=X_b[random_index:random_index+1] yi=y[random_index:random_index+1] gradients=2*xi.T.dot(xi.dot(theta)-yi) learning_rate=learning_schedule(epoch*m+i) 为了让越接近最优解的时候,调整的幅度越小,避免来回震荡 theta=theta-learning_rate*gradients 随着迭代的次数增多,调整的幅度自动减小 print(theta) 维度数据归一化:将数据统一化处理 最大值最小值归一化:把数据归到0到1之间 为了各个维度梯度可以同时收敛,基于梯度进行下降求解最优解都需要归一化处理 如果X1< 因为X1< 因为g1< 所以g越小,调整的幅度就越小 总结推导: X1< 过拟合:拟合过度,用算法生成的模型,很好的拟合了现有的数据样本即训练集数据,但是新的数据即测试集的数据预测的准确率反而降低了 防止过拟合,等价于提高模型的泛化能力或推广能力或者是举一反三的能力即提高模型的容错能力 举例: 学霸:有监督的机器学习 学神:有很强的学习能力,能自己找到学习的方法,无监督的机器学习 学渣:你的算法压根就没选对,数据预处理也没对,学习方法不对 学痴:做练习题都会,考试稍微一变化就不会,过拟合,没有泛化能力 模型参数W个数越少越好,模型参数W的值越小越好(如果X输入有误差,对预测的结果y影响很小),通过正则化惩罚项人为的修改已有的损失函数,比如使用L1、L2正则添加到loss func L1为多个维度的w绝对值加和,使用L1正则化会使权重W值两极分化于1或0也成为稀疏编码,可以进行降维,一般在数据进行模型训练之前会进行特征工程降维 L2为多个维度的w平方和,使用L2正则化会使权重W值整体偏小,由于特征工程已经进行降维所以一般使用L2 使用随机梯度下降SGD找找最优解的过程中,考虑惩罚项的影响 岭回归(Ridge Regression):使用L2方式人为的改变损失函数,使用惩罚项提高模型的泛化能力,但一定程度上降低了模型正确率即对训练集已有数据的拟合效果,但模型的目的是对未来新的数据进行预测,惩罚项中有超参数alpha即惩罚项的权重,可以通过调整alpha超参数根据需求来决定是注重模型的正确率还是模型的泛化能力 import numpy as np from sklearn.linear_model import Ridge 引入岭回归模块 from sklearn.linear_model import SGDRegressor 引入随机梯度下降模块 X = 2 * np.random.rand(100, 1) y = 4 + 3 * X + np.random.randn(100, 1) ridge_reg = Ridge(alpha=1, solver='sag') 获取超参数alpha为1批量梯度下降的岭回归对象 ridge_reg.fit(X, y) 传入X和Y矩阵 print(ridge_reg.predict(1.5)) 获取x为1.5的预测值 print(ridge_reg.intercept_) 获取截距即w0,传入的样本数据X矩阵中没有x0但Ridge初始化默认超参数fix_ intercept为True print(ridge_reg.coef_) 获取权重W矩阵 sgd_reg = SGDRegressor(penalty='l2', n_iter=1000) 获取正则化惩罚项为L2(正则化为l2的SGDRegressor与Ridge等价),迭代次数为1000的SGDRegressor对象 sgd_reg.fit(X, y.ravel()) 传入X和Y矩阵 print(sgd_reg.predict(1.5)) 获取x为1.5的预测值 print("W0=", sgd_reg.intercept_) 获取截距即w0,传入的样本数据X矩阵中没有x0但Ridge初始化默认超参数fix_ intercept为True print("W1=", sgd_reg.coef_) 获取权重W矩阵 Lasso使用L1正则化惩罚项改变损失函数 import numpy as np from sklearn.linear_model import Lasso from sklearn.linear_model import SGDRegressor X = 2 * np.random.rand(100, 1) y = 4 + 3 * X + np.random.randn(100, 1) lasso_reg = Lasso(alpha=0.15) lasso_reg.fit(X, y) print(lasso_reg.predict(1.5)) print(lasso_reg.coef_) sgd_reg = SGDRegressor(penalty='l1', max_iter=1000) sgd_reg.fit(X, y.ravel()) print(sgd_reg.predict(1.5)) print(sgd_reg.coef_) Elastic Net使用L1和L2两种正则化惩罚项改变损失函数,可以根据超参数修改L1和L2的权重 import numpy as np from sklearn.linear_model import ElasticNet from sklearn.linear_model import SGDRegressor X = 2 * np.random.rand(100, 1) y = 4 + 3 * X + np.random.randn(100, 1) elastic_net = ElasticNet(alpha=0.0001, l1_ratio=0.15) elastic_net.fit(X, y) print(elastic_net.predict(1.5)) sgd_reg = SGDRegressor(penalty='elasticnet', max_iter=1000) sgd_reg.fit(X, y.ravel()) print(sgd_reg.predict(1.5)) 线性回归算法一般选择顺序:Ridge Regression(L2正则化)、ElasticNet(即包含L1又包含L2)、Lasso Regression(L1正则化) 超参数alpha在Rideg类中是L2正则的权重、在Lasso类中是L1正则的权重、在ElasticNet和SGDRegressor里面是损失函数里面的alpha 超参数l1_ration在ElasticNet和SGDRegressor中是损失函数的p 多项式回归:PolynomialFeatures(多项式特征)不是做拟合的算法是做预处理的方法,转换数据继续升维(维度的次幂,通过degree超参数在原有的维度基础上增加高阶次幂维度),是为了让线性模型去拟合非线性的数据 升维是增加多个影响Y结果的因素,这样考虑的更全面,最终目的是要增加准确率 如果数据是非线性的变化可以使用非线性的算法生成的模型进行拟合,也可以使用PolynomialFeatures将非线性的数据进行变化,变成类似线性的变化,然后使用线性的模型进行拟合 import numpy as np import matplotlib.pyplot as plt from sklearn.preprocessing import PolynomialFeatures from sklearn.linear_model import LinearRegression m = 100 X = 6 * np.random.rand(m, 1) - 3 y = 0.5 * X ** 2 + X + 2 + np.random.randn(m, 1) plt.plot(X, y, 'b.') d = {1: 'g-', 2: 'r+', 10: 'y*'} for i in d: poly_features = PolynomialFeatures(degree=i, include_bias=False) 获取degree高阶没有截距(梯度下降算法中默认有截距为避免重复)多项式特征升维对象 X_poly = poly_features.fit_transform(X) 对矩阵X进行多项式特征转换 print(X[0]) print(X_poly[0]) print(X_poly[:, 0]) lin_reg = LinearRegression(fit_intercept=True) lin_reg.fit(X_poly, y) print(lin_reg.intercept_, lin_reg.coef_) y_predict = lin_reg.predict(X_poly) plt.plot(X_poly[:, 0], y_predict, d[i]) plt.show() 进行模型拟合时需要观测注意数据多样性,采样要均匀是为了模型的功能是对任何年龄段的人都有一个好的预测,读取的数据集就需要包含各个年龄段得数据,而且各个年龄段的数据均匀,防止过拟合 import pandas as pd 引入数据处理模块(pandas的DataFrame数据结构可以被Spark获取进行处理) import matplotlib.pyplot as plt from sklearn.preprocessing import PolynomialFeatures from sklearn.linear_model import LinearRegression data = pd.read_csv('./insurance.csv') 读取文件 print(type(data)) print(data.head()) print(data.tail()) # describe做简单的统计摘要 print(data.describe()) 查看数据简单统计摘要 # 采样要均匀 data_count = data['age'].value_counts() print(data_count) # data_count[:10].plot(kind='bar') # plt.show() # plt.savefig('./temp') print(data.corr()) 查看数据之间的相关性,默认使用计算数值型的pearson公式 reg = LinearRegression() x = data[['age', 'sex', 'bmi', 'children', 'smoker', 'region']] y = data['charges'] # python3.6 报错 sklearn ValueError: could not convert string to float: 'northwest',加入一下几行解决 x = x.apply(pd.to_numeric, errors='coerce') 将字符串数据转换为数值型 y = y.apply(pd.to_numeric, errors='coerce') x.fillna(0, inplace=True) 将空的数据转换为0 y.fillna(0, inplace=True) poly_features = PolynomialFeatures(degree=3, include_bias=False) X_poly = poly_features.fit_transform(x) reg.fit(X_poly, y) print(reg.coef_) print(reg.intercept_) y_predict = reg.predict(X_poly) plt.plot(x['age'], y, 'b.') plt.plot(X_poly[:, 0], y_predict, 'r.') plt.show() Pearson相关系数:测量两组变量之间的线性相关性,区间范围为-1(负相关)到1(正相关)之间,相关系数越接近于0,说明越不相关,两个维度之间相关系数接近于1,可以去掉其中一个维度进行降维,某个维度和结果Y之间的相关系数接近于0,可以去掉这个维度进行降维 多元线性回归(Ridge、Lasso、ElasticNet)用于回归预测,逻辑回归(Logistic Regression)用于分类任务 回归预测损失函数为平方均值损失函数MSE 逻辑回归(二分类):函数曲线范围在[0,1]之间,大于大于0.5分成两类 t=WTX 熵是一种测量分子不稳定性的指标,分子运动越不稳定,熵就越大,来自热力学 熵是一种测量信息量的单位,信息熵,包含的信息越多,熵就越大,来自信息论,香农 熵是一种测量不确定性的单位,不确定性越大,概率越小,熵就越大 概率越小,熵会越大 逻辑回归本质是多元线性回归,应用了多元线性回归的公式,把多元线性回归的结果交给sigmoid函数去进行缩放,逻辑回归的损失函数推导的导函数,整个形式上和多元线性回归基本一致,只是y_hat求解公式包含了一个sigmoid过程 逻辑回归的分类损失函数是交叉熵-y*logP,损失函数loss func = (-y*logP + -(1-y)*log(1-P)),loss func损失最小即逻辑回归二分类找到最优解,可以使用梯度下降法来求解最优解 由于线性回归区间是负无穷到正无穷的可以按照0来分成两部分代入sigmoid公式后t=0,y=0.5,所有逻辑回归阈值是0.5 import numpy as np from sklearn import datasets 引入数据集模块 from sklearn.linear_model import LogisticRegression 引入逻辑回归模块 from sklearn.model_selection import GridSearchCV 引入网格搜索交叉验证模块 import matplotlib.pyplot as plt from time import time 引入时间模块 iris = datasets.load_iris() 获取数据集中的数据 print(list(iris.keys())) 获取数据集中的键值 print(iris['DESCR']) 获取数据集的变量名 print(iris['feature_names']) 获取数据集的描述 X = iris['data'][:, 3:] 获取数据集中矩阵指定行列 print(X) print(iris['target']) 获取数据中的目标即分类号 y = iris['target'] # y = (iris['target'] == 2).astype(np.int) print(y) # Utility function to report best scores # def report(results, n_top=3): # for i in range(1, n_top + 1): # candidates = np.flatnonzero(results['rank_test_score'] == i) # for candidate in candidates: # print("Model with rank: {0}".format(i)) # print("Mean validation score: {0:.3f} (std: {1:.3f})".format( # results['mean_test_score'][candidate], # results['std_test_score'][candidate])) # print("Parameters: {0}".format(results['params'][candidate])) # print("") # start = time() # param_grid = {"tol": [1e-4, 1e-3, 1e-2], # "C": [0.4, 0.6, 0.8]} log_reg = LogisticRegression(multi_class='ovr', solver='sag') 获取逻辑回归二分类ovr(multi_class多分类soft-max回归)使用梯度下降法的对象 # grid_search = GridSearchCV(log_reg, param_grid=param_grid, cv=3) 获取对log_reg模型算法对象超参数为param_grid使用cv折交叉验证的网格搜索验证对象 log_reg.fit(X, y) # print("GridSearchCV took %.2f seconds for %d candidate parameter settings." # % (time() - start, len(grid_search.cv_results_['params']))) # report(grid_search.cv_results_) X_new = np.linspace(0, 3, 1000).reshape(-1, 1) 生成测试集数据,生成1000个从0到3区间平均分割区间段的数值 print(X_new) y_proba = log_reg.predict_proba(X_new) 预测分类概率值 y_hat = log_reg.predict(X_new) 预测分类号 print(y_proba) print(y_hat) plt.plot(X_new, y_proba[:, 2], 'g-', label='Iris-Virginica') plt.plot(X_new, y_proba[:, 1], 'r-', label='Iris-Versicolour') plt.plot(X_new, y_proba[:, 0], 'b--', label='Iris-Setosa') plt.show() print(log_reg.predict([[1.7], [1.5]])) 逻辑回归进行多分类实质是通过改变数据y的值将多分类转换为多个二分类,多分类的权重W矩阵是多个二分类所有的权重W,例如进行三分类需要同时训练三个互相不影响的二分类模型,模型有n个维度,那三分类w参数的个数就会是(n+1)*3个参数 傅里叶变化:将振幅、时间、频率维度的数据转换为振幅和频率维度的数据 使用logistic regression处理音乐数据,音乐数据训练样本的获得和使用快速傅里叶变换(FFT)预处理的方法 # 音乐数据分类 import numpy as np from sklearn import linear_model, datasets import matplotlib.pyplot as plt from scipy.stats import norm from scipy import fft from scipy.io import wavfile def create_fft(g, n): rad = "d:/genres/"+g+"/converted/"+g+"."+str(n).zfill(5)+".au.wav" sample_rate, X = wavfile.read(rad) 获取音乐数据 fft_features = abs(fft(X)[:1000]) 音乐数据进行傅里叶转换 sad = "d:/trainset/"+g+"."+str(n).zfill(5) + ".fft" np.save(sad, fft_features) 保存转换后的数据 genre_list = ["classical", "jazz", "country", "pop", "rock", "metal"] for g in genre_list: for n in range(100): create_fft(g, n) genre_list = ["classical", "jazz", "country", "pop", "rock", "metal"] X = [] Y = [] for g in genre_list: for n in range(100): rad = "d:/StudyMaterials/python/python-sklearn/trainset/"+g+"."+str(n).zfill(5)+ ".fft"+".npy" fft_features = np.load(rad) X.append(fft_features) 构建音乐数据集的X Y.append(genre_list.index(g)) 构建音乐数据集的Y X = np.array(X) 将X列表转换为X矩阵 Y = np.array(Y) 将Y列表转换为Y矩阵 import random randomIndex=random.sample(range(len(Y)),int(len(Y)*8/10)) 拆分数据集为训练数据集和测试数据集 trainX=[];trainY=[];testX=[];testY=[] for i in range(len(Y)): if i in randomIndex: trainX.append(X[i]) trainY.append(Y[i]) else: testX.append(X[i]) testY.append(Y[i]) from sklearn.linear_model import LogisticRegression model = LogisticRegression() 获取逻辑回归默认线性代数的解析解(数据量少可以使用,数据量大无法直接解析解进行计算使用梯度下降) model.fit(X, Y) # predictYlogistic=map(lambda x:logclf.predict(x)[0],testX) # 可以采用Python内建的持久性模型 pickle 来保存scikit的模型 import pickle 引入保存scikit的模型的模块 s = pickle.dumps(clf) clf2 = pickle.loads(s) clf2.predict(X[0]) 非线性算法神经网络(仿生)ANN(artificial neural network)进行预测,神经网络是深度学习的基础,多层感知机MLP(multiple layer percepton)、卷积神级网络CNN(常用于图像识别)、循环神经网络RNN 激活函数:将神经元的净输入信号转换成单一的输出信号以便进一步在神经网络中传播 网络拓扑:描述神经网络模型中神经元的数量以及层数和神经元之间的连接方式 训练算法:指定如何设置连接权重,以便抑制或增加神经元在输入信号中的比重 激活函数的选择:对应神经元中的逻辑,两部分相乘相加和非线性的变化,相乘相加固定不变,非线性的变化需要根据效果进行选择 网络拓扑结构的选择:处理更加复杂的问题需要更多的网络层,需要每层上设置更多的人工神经元,神经网络拓扑结构的第一层为输入层最后一层为输出层,中间层成为隐藏层 训练算法的选择:在求解神经网络模型的时候即求解所有神经元的权重W,需要选择优化算法提高运算速度,可以使用SGD算法(硬件上可以使用GPU代替CPU进行计算) 激活函数常用有:Sigmoid函数(0到1之间)、Tangent函数(-1到1之间)、Relu函数max(0,x) 没有隐藏层的神经网络即单层神经网络实质是逻辑回归 神经网络算法的隐藏层增加了推理演绎的能力,随着隐藏层增多,推理和演绎的过程也增多,考虑的更深入,隐藏层的隐藏节点(神经元)数量比上一层的节点多,相当于进行升维考虑更多因素考虑更全面,隐藏层的隐藏节点数量比上一层的节点少,相当于降维进行归纳总结 from sklearn.neural_network import MLPClassifier 引入多层感知机分类算法模块 X = [[0., 0.], [1., 1.]] y = [0, 1] clf = MLPClassifier(solver='sgd', alpha=1e-5, activation='logistic', hidden_layer_sizes=(5, 2), max_iter=2000, tol=1e-4) 获取sgd随机梯度下降优化算法L2正则化激活函数为logistic隐藏层为(5,2)两层最大迭代次数2000梯度阈值1e-4的多层感知机分类算法对象 clf.fit(X, y) predicted_value = clf.predict([[2., 2.], [-1., -2.]]) print(predicted_value) predicted_proba = clf.predict_proba([[2., 2.], [-1., -2.]]) print(predicted_proba) print([coef.shape for coef in clf.coefs_]) 获取神经网络中权重的形状 print([coef for coef in clf.coefs_]) 获取神经网络权重值 soft-max回归基于多元线性回归进行多分类的算法 K为类别分数 soft-max回归的损失函数为交叉熵 逻辑回归近似是soft-max回归k=2时的特殊情况,soft-max回归每个类别之间互相关联 数据集一般分为训练集(训练和评估验证)和测试集 交叉验证(Cross-Validation)用于将训练集大部分数据样本进行建立模型,小部分训练集对建立的模型进行预报评估记录预报误差平方和 K折交叉验证:将训练集数据随机分为K份,每份作为验证集进行一次训练模型评估,找到超参数中K折交叉验证预报误差最小的超参数组合即找到模型最适合的超参数,由于超参数的组合多和K的数量会导致迭代次数多时间长 决策树和随机森林是非线性有监督分类模型 决策树(Decision Tree)使用的数据样本需要离散化:连续的数据可以根据区间段分割的方式将数据离散化到M+1种数据形式中,离散数据使用One-hot编码进行离散化成2^M中数据形式 决策树生成:数据样本按照每个维度进行分裂递归过程,将相同类别的数据归到树的一边,找到树的叶子节点中纯度最高的维度根节点的决策树为最优决策树 决策树分类纯度指标有:基尼系数(Gini Impurity)、熵(Entropy)和方差(Variance) 单颗决策树的缺点:运算量大,需要一次加载所有数据进内存并且找寻分割条件非常耗费资源的工作,训练样本中出现异常数据时,将会对决策树产生很大影响即抗干扰能力差,逻辑回归通过正则化进行泛化容错性好,决策树不能像逻辑回归可以给出分类的概率 决策树解决方法:减少决策树所需训练样本,随机采样降低异常数据的影响 随机森林(Random Forests):随机抽取数据集中多个部分数据样本生成多个决策树,将多个决策树分类结果汇总按照少数服从多数机制进行最终分类 逻辑回归是软分类输出有概率意义线性模型抗干扰能力强 随机森林是硬分类输出无概率意义非线性模型抗干扰能力弱 决策树生成时可以通过超参数对树进行预剪枝调节树的层数和叶子节点数量来提高数的泛化能力防止过拟合,决策树生成可以进行后剪枝进行提高泛化能力 单个决策树: import pandas as pd import numpy as np from sklearn.datasets import load_iris 引入数据集模块 from sklearn.tree import DecisionTreeClassifier 引入决策树分类模块 from sklearn.tree import export_graphviz from sklearn.tree import DecisionTreeRegressor引入决策树回归模块 from sklearn.model_selection import train_test_split 引入数据集训练与测试数据分割模块 from sklearn.metrics import accuracy_score 引入评估准确率模块 import matplotlib.pyplot as plt import matplotlib as mpl iris = load_iris() 导入数据集 data = pd.DataFrame(iris.data) 转换成DataFrame数据类型 data.columns = iris.feature_names 数据加入列名称 data['Species'] = load_iris().target # print(data) x = data.iloc[:, :2] # 花萼长度和宽度 y = data.iloc[:, -1] # y = pd.Categorical(data[4]).codes # print(x) # print(y) x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.75, random_state=42) 数据集切分成75%训练集25%测试集随机切分种子为42 tree_clf = DecisionTreeClassifier(max_depth=8, criterion='entropy') 获取决策树树最大层数为8纯度标准为entropy的模型对象 tree_clf.fit(x_train, y_train) y_test_hat = tree_clf.predict(x_test) print("acc score:", accuracy_score(y_test, y_test_hat)) 获取预测的正确率 """ export_graphviz( tree_clf, out_file="./iris_tree.dot", feature_names=iris.feature_names[:2], class_names=iris.target_names, rounded=True, filled=True ) # ./dot -Tpng ~/PycharmProjects/mlstudy/bjsxt/iris_tree.dot -o ~/PycharmProjects/mlstudy/bjsxt/iris_tree.png """ print(tree_clf.predict_proba([[5, 1.5]])) print(tree_clf.predict([[5, 1.5]])) depth = np.arange(1, 15) err_list = [] for d in depth: 遍历超参数树深度层数找到最优的超参数 clf = DecisionTreeClassifier(criterion='entropy', max_depth=d) clf.fit(x_train, y_train) y_test_hat = clf.predict(x_test) result = (y_test_hat == y_test) if d == 1: print(result) err = 1 - np.mean(result) print(100 * err) err_list.append(err) print(d, ' 错误率:%.2f%%' % (100 * err)) mpl.rcParams['font.sans-serif'] = ['SimHei'] 设置字体为SimHei plt.figure(facecolor='w') 图底色白色 plt.plot(depth, err_list, 'ro-', lw=2) 设置图横坐标纵坐标红色连接圆圈点线宽度2 plt.xlabel('决策树深度', fontsize=15) 设置横坐标标签 plt.ylabel('错误率', fontsize=15) 纵坐标标签 plt.title('决策树深度和过拟合', fontsize=18) 图标签 plt.grid(True) plt.show() # tree_reg = DecisionTreeRegressor(max_depth=2) # tree_reg.fit(X, y) 随机森林: from sklearn.ensemble import RandomForestClassifier 引入随机森林分类器模块 from sklearn.datasets import make_moons from sklearn.model_selection import train_test_split from sklearn.ensemble import BaggingClassifier 引入bagging思想并行分类模块 from sklearn.tree import DecisionTreeClassifier from sklearn.metrics import accuracy_score from sklearn.datasets import load_iris iris = load_iris() X = iris.data[:, :2] # 花萼长度和宽度 y = iris.target X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42) rnd_clf = RandomForestClassifier(n_estimators=15, max_leaf_nodes=16, n_jobs=1) 获取15个决策树最大叶子节点16线程数1的随机森林对象 rnd_clf.fit(X_train, y_train) bag_clf = BaggingClassifier( 获取决策树并行对象与RandomForestClassifier一致,splitter决策树维度方式,max_samples随机抽取样本数量 DecisionTreeClassifier(splitter="random", max_leaf_nodes=16), n_estimators=15, max_samples=1.0, bootstrap=True, n_jobs=1 ) bag_clf.fit(X_train, y_train) y_pred_rf = rnd_clf.predict(X_test) y_pred_bag = bag_clf.predict(X_test) print(accuracy_score(y_test, y_pred_rf)) print(accuracy_score(y_test, y_pred_bag)) # Feature Importance iris = load_iris() rnd_clf = RandomForestClassifier(n_estimators=500, n_jobs=-1) rnd_clf.fit(iris["data"], iris['target']) for name, score in zip(iris['feature_names'], rnd_clf.feature_importances_): 分类特征与结果关联性程度和特征名联合,可以进行特征提取进行降维 print(name, score) bagging思想并行分类: from sklearn.ensemble import RandomForestClassifier from sklearn.ensemble import VotingClassifier from sklearn.linear_model import LogisticRegression from sklearn.svm import SVC from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split from sklearn.ensemble import BaggingClassifier 引入bagging并行模块 from sklearn.tree import DecisionTreeClassifier from sklearn.metrics import accuracy_score log_clf = LogisticRegression() rnd_clf = RandomForestClassifier() svm_clf = SVC() voting_clf = VotingClassifier( 投票分类器,hard硬投票即少数服从多数,整合前三个分类器 estimators=[('lr', log_clf), ('rf', rnd_clf), ('svc', svm_clf)], voting='hard' ) iris = load_iris() X = iris.data[:, :2] # 花萼长度和宽度 y = iris.target # X, y = make_moons() X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42) voting_clf.fit(X, y) for clf in (log_clf, rnd_clf, svm_clf, voting_clf): clf.fit(X_train, y_train) y_pred = clf.predict(X_test) print(clf.__class__.__name__, accuracy_score(y_test, y_pred)) bag_clf = BaggingClassifier( DecisionTreeClassifier(), n_estimators=500, max_samples=1.0, bootstrap=True, n_jobs=1 ) bag_clf.fit(X_train, y_train) y_pred = bag_clf.predict(X_test) print(y_pred) y_pred_proba = bag_clf.predict_proba(X_test) print(y_pred_proba) print(accuracy_score(y_test, y_pred)) # oob bag_clf = BaggingClassifier( DecisionTreeClassifier(), n_estimators=500, bootstrap=True, n_jobs=1, oob_score=True ) bag_clf.fit(X_train, y_train) print(bag_clf.oob_score_) y_pred = bag_clf.predict(X_test) print(accuracy_score(y_test, y_pred)) print(bag_clf.oob_decision_function_) 决策树回归:将树叶子节点中的数值取平均值作为回归预测值 import numpy as np from sklearn.tree import DecisionTreeRegressor 引入决策树回归模块 import matplotlib.pyplot as plt N = 100 x = np.random.rand(N) * 6 - 3 x.sort() y = np.sin(x) + np.random.rand(N) * 0.05 非线性函数变化 print(y) x = x.reshape(-1, 1) print(x) dt_reg = DecisionTreeRegressor(criterion='mse', max_depth=3) 获取损失函数为mse的决策树回归对象 dt_reg.fit(x, y) x_test = np.linspace(-3, 3, 50).reshape(-1, 1) y_hat = dt_reg.predict(x_test) plt.plot(x, y, "y*", label="actual") plt.plot(x_test, y_hat, "b-", linewidth=2, label="predict") plt.legend(loc="upper left") plt.grid() plt.show() # plt.savefig("./temp_decision_tree_regressor") # 比较不同深度的决策树 depth = [2, 4, 6, 8, 10] color = 'rgbmy' dt_reg = DecisionTreeRegressor() plt.plot(x, y, "ko", label="actual") x_test = np.linspace(-3, 3, 50).reshape(-1, 1) for d, c in zip(depth, color): dt_reg.set_params(max_depth=d) dt_reg.fit(x, y) y_hat = dt_reg.predict(x_test) plt.plot(x_test, y_hat, '-', color=c, linewidth=2, label="depth=%d" % d) plt.legend(loc="upper left") plt.grid(b=True) plt.show() # plt.savefig("./temp_compare_decision_tree_depth") 分类评估指标: 混淆矩阵:每一列代表了预测类别,每一列的总数表示预测为该类别的数据的数目,每一行代表了数据的真实归属类别,每一行的数据总数表示该类别的数据实例的数目,每一列中的数值表示真实数据被预测为该类的数目 True positives(TP):被正确地划分为正例的个数,即实际为正例且被分类器划分为正例的实例数(样本数) False positives(FP):被错误地划分为正例的个数,即实际为负例但被分类器划分为正例的实例数 False negatives(FN):被错误地划分为负例的个数,即实际为正例但被分类器划分为负例的实例数 True negatives(TN):被正确地划分为负例的个数,即实际为负例且被分类器划分为负例的实例数 正确率(accuracy),accuracy=(TP+TN)/(P+N)即分类正确的数量除以样本总数量 错误率(error rate):被分类器错分的比例,error rate = (FP+FN)/(P+N),accuracy=1-error rate 准确率(precision),precision=TP/(TP+FP)即正确的分类为正例的数量除以分为正例的总数 召回率(recall),recall=TP/(TP+FN)=TP/P=sensitive即正确的分类为正例的数量除以实际为正例的总数 灵敏度(sensitive),sensitive = TP/P即所有正例中被分对的比例,衡量了分类器对正例的识别能力 特效度(specificity),specificity = TN/N即所有负例中被分对的比例,衡量了分类器对负例的识别能力 准确率与召回率之间TradeOff相互制约,两者结合的评估指标F-Measure(F1-Score): F1=2/(1/precision+1/recall)=2precision*recall/(precision+recall)=TP/(TP+(FN+FP)/2) ROC曲线:以FPR为横坐标TPR为纵坐标的曲线,曲线越趋近与(0,1)点模型分类越准确 TPR(True Positive Rate):所有实际为正例的样本中被正确的分类为正例的比例,TPR=TP/(TP+FN) FPR(False Positive Rate):所有实际为负例的样本中被错误的分类为正例的比例,FPR=FP/(FP+TN) AUC面积:以FPR为横坐标TPR为纵坐标的曲线与横坐标的面积 from sklearn.datasets import fetch_mldata引入数据集模块 import matplotlib import matplotlib.pyplot as plt import numpy as np from sklearn.linear_model import SGDClassifier引入SGD优化算法的分类模块 from sklearn.model_selection import StratifiedKFold引入K折交叉验证模块 from sklearn.base import clone from sklearn.model_selection import cross_val_score引入交叉验证分数模块 from sklearn.base import BaseEstimator from sklearn.model_selection import cross_val_predict引入交叉验证类别模块 from sklearn.metrics import confusion_matrix引入混淆矩阵模块 from sklearn.metrics import precision_score引入准确率模块 from sklearn.metrics import recall_score引入召回率模块 from sklearn.metrics import f1_score引入F-Measure评估模块 from sklearn.metrics import precision_recall_curve引入准确率与召回率曲线模块 from sklearn.metrics import roc_curve引入ROC曲线评估模块 from sklearn.metrics import roc_auc_score引入AUC面积评估模块 from sklearn.ensemble import RandomForestClassifier引入随机森林分类模块 mnist = fetch_mldata('MNIST original', data_home='test_data_home')获取原始图片数据集,数据目录为test_data_home,目录中不存在数据集自动从mldata.org下载 print(mnist) X, y = mnist['data'], mnist['target'] print(X.shape, y.shape) some_digit = X[36000] print(some_digit) some_digit_image = some_digit.reshape(28, 28)改变矩阵形状 print(some_digit_image) # plt.imshow(some_digit_image, cmap=matplotlib.cm.binary, # interpolation='nearest')绘制矩阵图像 # plt.axis('off') # plt.show() X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[:60000] shuffle_index = np.random.permutation(60000)无返回的生成指定数值个随机数即从0到指定数值随机排序 X_train, y_train = X_train[shuffle_index], y_train[shuffle_index] y_train_5 = (y_train == 5) y_test_5 = (y_test == 5) print(y_test_5) sgd_clf = SGDClassifier(loss='log', random_state=42, max_iter=1000, tol=1e-4)获取随机梯度下降优化分类的模型 sgd_clf.fit(X_train, y_train_5) print(sgd_clf.predict([some_digit])) # skfolds = StratifiedKFold(n_splits=3, random_state=42)获取n_splits折交叉验证对象 # for train_index, test_index in skfolds.split(X_train, y_train_5):切分数据集的训练集和验证集 # clone_clf = clone(sgd_clf) # X_train_folds = X_train[train_index]获取X的训练集 # y_train_folds = y_train_5[train_index] 获取Y的训练集 # X_test_folds = X_train[test_index] 获取X的验证集 # y_test_folds = y_train_5[test_index] 获取X的验证集 # clone_clf.fit(X_train_folds, y_train_folds) # y_pred = clone_clf.predict(X_test_folds) # print(y_pred) # n_correct = sum(y_pred == y_test_folds) # print(n_correct / len(y_pred)) # print(cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring='accuracy'))获取cv折交叉验证计算scoring评估值 # class Never5Classifier(BaseEstimator):自定义全部分为负例的模型,自定义模型需要继承BaseEstimator # def fit(self, X, y=None): # pass # def predict(self, X): # return np.zeros((len(X), 1), dtype=bool) # never_5_clf = Never5Classifier() # print(cross_val_score(never_5_clf, X_train, y_train_5, cv=3, scoring='accuracy')) # y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)获取cv折交叉验证训练模型 # print(confusion_matrix(y_train_5, y_train_pred))获取混淆矩阵 # y_train_perfect_prediction = y_train_5 # print(confusion_matrix(y_train_5, y_train_perfect_prediction)) # print(precision_score(y_train_5, y_train_pred)) # print(recall_score(y_train_5, y_train_pred)) # print(sum(y_train_pred)) # print(f1_score(y_train_5, y_train_pred)) sgd_clf.fit(X_train, y_train_5) y_scores = sgd_clf.decision_function([some_digit])获取分类模型的决策边界 print(y_scores) threshold = 0 y_some_digit_pred = (y_scores > threshold) print(y_some_digit_pred) threshold = 200000 y_some_digit_pred = (y_scores > threshold) print(y_some_digit_pred) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method='decision_function')获取交叉验证的决策函数即分类前的值 print(y_scores) precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)获取准确率和召回率 print(precisions, recalls, thresholds) def plot_precision_recall_vs_threshold(precisions, recalls, thresholds): plt.plot(thresholds, precisions[:-1], 'b--', label='Precision') plt.plot(thresholds, recalls[:-1], 'r--', label='Recall') plt.xlabel("Threshold") plt.legend(loc='upper left') plt.ylim([0, 1]) # plot_precision_recall_vs_threshold(precisions, recalls, thresholds) # plt.show() # y_train_pred_90 = (y_scores > 70000) # print(precision_score(y_train_5, y_train_pred_90)) # print(recall_score(y_train_5, y_train_pred_90)) fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)获取ROC曲线 def plot_roc_curve(fpr, tpr, label=None): plt.plot(fpr, tpr, linewidth=2, label=label) plt.plot([0, 1], [0, 1], 'k--') plt.axis([0, 1, 0, 1]) plt.xlabel('False Positive Rate') plt.ylabel('True positive Rate') # plot_roc_curve(fpr, tpr) # plt.show() print(roc_auc_score(y_train_5, y_scores))获取ROC曲线AUC的面积 forest_clf = RandomForestClassifier(random_state=42) y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3, method='predict_proba') y_scores_forest = y_probas_forest[:, 1] fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5, y_scores_forest) plt.plot(fpr, tpr, 'b:', label='SGD') plt.plot(fpr_forest, tpr_forest, label='Random Forest') plt.legend(loc='lower right') plt.show() print(roc_auc_score(y_train_5, y_scores_forest)) 无监督学习聚类:按照相似度对数据进行聚簇(cluster)划分,N个样本映射到K个簇中,每个簇至少有一个样本,一个样本只能属于一个簇,先给定一个初始划分,迭代改变样本和簇的关系,聚类的副产品可以做异常值检测 相似度指标有: 多维空间向量点之间的距离(闵可夫斯基距离公式): 当p为2时即欧式距离(二维空间距离公式): 当p为1时即曼哈顿距离(Block Distance) 三维空间距离公式: 当p趋近于无穷大时即切比雪夫距离(由于维度无穷多,所有维度差值最大的维度距离差可以近似距离) Jaccard相关系数(Jaccard similarity coefficient)比较有限样本集之间的相似度: 余弦相似度:余弦值区间为[-1,1],余弦值接近-1相似度越小接近0向量正交接近1相似度越大,一般用于文档相似度聚类 Pearson相关系数(线性相关性):两个变量之间的协方差和标准差的商,Xi与Yi为0时即为余弦相似度公式 相对熵:两个集合相同相对熵相似度系数为0 K-Means聚类平均数算法:选择K个初始簇中心(随机或者先验知识即经验),迭代计算样本与每个聚类中心的距离和所属聚类的样本均值即簇中心点直到簇中心点不发生变化认为模型收敛 划分: 聚类中心点: K-Mediods聚类中位数算法:对K-Means聚类算法的改进以中位数作为簇中心点 二分K-Means算法:两个簇样本数量少簇中心近损失函数MSE小合并为一个簇,簇中心离其他簇中心远样本数量大损失函数MSE大分为多个簇 K-Means++:对K-Means聚类算法的改进,初始化中心点均有随机,使用肘部法找到最合适的K即簇的数量 K均值损失函数: K均值假设符合高斯混合分布,高斯混合分布不是线性回归凹函数,有多个极小值,可以用淬火法或遗传算法计算全局最优解,K-Means算法是根据样本到簇中心点的距离进行聚类所以算法更适合对近似圆形规则的样本进行聚类 import numpy as np import matplotlib.pyplot as plt import sklearn.datasets as ds import matplotlib.colors from sklearn.cluster import KMeans引入K-Means模块 from sklearn.cluster import MiniBatchKMeans引入小批量K-Means模块(计算簇中心不使用所有样本随机部分样本求簇中心,计算速度快,数据量大可以使用) def expand(a, b): d = (b - a) * 0.1 return a-d, b+d if __name__ == "__main__": N = 400 centers = 4 data, y = ds.make_blobs(N, n_features=2, centers=centers, random_state=2)生成N个样本n_features个维度centers个簇中心的聚类模拟数据 data2, y2 = ds.make_blobs(N, n_features=2, centers=centers, cluster_std=(1, 2.5, 0.5, 2), random_state=2) 生成样本数据方差为cluster_std(即数据分散程度)的聚类模拟数据 data3 = np.vstack((data[y == 0][:], data[y == 1][:50], data[y == 2][:20], data[y == 3][:5]))获取簇样本数量不一致的聚类模拟数据 y3 = np.array([0] * 100 + [1] * 50 + [2] * 20 + [3] * 5) cls = KMeans(n_clusters=4, init='k-means++')获取簇中心即K为n_clusters初始化使用init的k-means对象 y_hat = cls.fit_predict(data)训练模型并获取预测值 y2_hat = cls.fit_predict(data2) y3_hat = cls.fit_predict(data3) m = np.array(((1, 1), (1, 3))) data_r = data.dot(m)对矩阵进行旋转 y_r_hat = cls.fit_predict(data_r) matplotlib.rcParams['font.sans-serif'] = [u'SimHei'] matplotlib.rcParams['axes.unicode_minus'] = False cm = matplotlib.colors.ListedColormap(list('rgbm')) plt.figure(figsize=(9, 10), facecolor='w') plt.subplot(421) plt.title(u'原始数据') plt.scatter(data[:, 0], data[:, 1], c=y, s=30, cmap=cm, edgecolors='none')绘制散点图 x1_min, x2_min = np.min(data, axis=0) x1_max, x2_max = np.max(data, axis=0) x1_min, x1_max = expand(x1_min, x1_max) x2_min, x2_max = expand(x2_min, x2_max) plt.xlim((x1_min, x1_max)) plt.ylim((x2_min, x2_max)) plt.grid(True) plt.subplot(422) plt.title(u'KMeans++聚类') plt.scatter(data[:, 0], data[:, 1], c=y_hat, s=30, cmap=cm, edgecolors='none') plt.xlim((x1_min, x1_max)) plt.ylim((x2_min, x2_max)) plt.grid(True) plt.subplot(423) plt.title(u'旋转后数据') plt.scatter(data_r[:, 0], data_r[:, 1], c=y, s=30, cmap=cm, edgecolors='none') x1_min, x2_min = np.min(data_r, axis=0) x1_max, x2_max = np.max(data_r, axis=0) x1_min, x1_max = expand(x1_min, x1_max) x2_min, x2_max = expand(x2_min, x2_max) plt.xlim((x1_min, x1_max)) plt.ylim((x2_min, x2_max)) plt.grid(True) plt.subplot(424) plt.title(u'旋转后KMeans++聚类') plt.scatter(data_r[:, 0], data_r[:, 1], c=y_r_hat, s=30, cmap=cm, edgecolors='none') plt.xlim((x1_min, x1_max)) plt.ylim((x2_min, x2_max)) plt.grid(True) plt.subplot(425) plt.title(u'方差不相等数据') plt.scatter(data2[:, 0], data2[:, 1], c=y2, s=30, cmap=cm, edgecolors='none') x1_min, x2_min = np.min(data2, axis=0) x1_max, x2_max = np.max(data2, axis=0) x1_min, x1_max = expand(x1_min, x1_max) x2_min, x2_max = expand(x2_min, x2_max) plt.xlim((x1_min, x1_max)) plt.ylim((x2_min, x2_max)) plt.grid(True) plt.subplot(426) plt.title(u'方差不相等KMeans++聚类') plt.scatter(data2[:, 0], data2[:, 1], c=y2_hat, s=30, cmap=cm, edgecolors='none') plt.xlim((x1_min, x1_max)) plt.ylim((x2_min, x2_max)) plt.grid(True) plt.subplot(427) plt.title(u'数量不相等数据') plt.scatter(data3[:, 0], data3[:, 1], s=30, c=y3, cmap=cm, edgecolors='none') x1_min, x2_min = np.min(data3, axis=0) x1_max, x2_max = np.max(data3, axis=0) x1_min, x1_max = expand(x1_min, x1_max) x2_min, x2_max = expand(x2_min, x2_max) plt.xlim((x1_min, x1_max)) plt.ylim((x2_min, x2_max)) plt.grid(True) plt.subplot(428) plt.title(u'数量不相等KMeans++聚类') plt.scatter(data3[:, 0], data3[:, 1], c=y3_hat, s=30, cmap=cm, edgecolors='none') plt.xlim((x1_min, x1_max)) plt.ylim((x2_min, x2_max)) plt.grid(True) plt.tight_layout(2, rect=(0, 0, 1, 0.97)) plt.suptitle(u'数据分布对KMeans聚类的影响', fontsize=18) # https://github.com/matplotlib/matplotlib/issues/829 # plt.subplots_adjust(top=0.92) plt.show() # plt.savefig('cluster_kmeans') 使用K-Means算法对图片像素进行聚类256中颜色即对减少图像损失程度下对图片压缩: from PIL import Image引入图像模块 import numpy as np from sklearn.cluster import KMeans import matplotlib import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D def restore_image(cb, cluster, shape): row, col, dummy = shape image = np.empty((row, col, 3)) index = 0 for r in range(row): for c in range(col): image[r, c] = cb[cluster[index]] index += 1 return image def show_scatter(a): N = 10 print('原始数据:\n', a) density, edges = np.histogramdd(a, bins=[N,N,N], range=[(0,1), (0,1), (0,1)]) density /= density.max() x = y = z = np.arange(N) d = np.meshgrid(x, y, z) fig = plt.figure(1, facecolor='w') ax = fig.add_subplot(111, projection='3d') ax.scatter(d[1], d[0], d[2], c='r', s=100*density, marker='o', depthshade=True) ax.set_xlabel(u'红色分量') ax.set_ylabel(u'绿色分量') ax.set_zlabel(u'蓝色分量') plt.title(u'图像颜色三维频数分布', fontsize=20) plt.figure(2, facecolor='w') den = density[density > 0] den = np.sort(den)[::-1] t = np.arange(len(den)) plt.plot(t, den, 'r-', t, den, 'go', lw=2) plt.title(u'图像颜色频数分布', fontsize=18) plt.grid(True) plt.show() if __name__ == '__main__': matplotlib.rcParams['font.sans-serif'] = [u'SimHei'] matplotlib.rcParams['axes.unicode_minus'] = False num_vq = 2 im = Image.open('../data/Lena.png') # flower2.png(200)/lena.png(50)获取图片 image = np.array(im).astype(np.float) / 255 image = image[:, :, :3]获取图片三维矩阵 image_v = image.reshape((-1, 3))图片像素转换成二维矩阵 model = KMeans(num_vq)获取K为256的K-Means聚类模型 show_scatter(image_v) N = image_v.shape[0] # 图像像素总数 # 选择足够多的样本(如1000个),计算聚类中心 idx = np.random.randint(0, N, size=1000) image_sample = image_v[idx] model.fit(image_sample)随机抽取1000个像素点进行聚类训练模型 c = model.predict(image_v) # 聚类结果 print('聚类结果:\n', c) print('聚类中心:\n', model.cluster_centers_) plt.figure(figsize=(15, 8), facecolor='w') plt.subplot(121) plt.axis('off') plt.title(u'原始图片', fontsize=18) plt.imshow(image) # plt.savefig('1.png') plt.subplot(122) vq_image = restore_image(model.cluster_centers_, c, image.shape) plt.axis('off') plt.title(u'矢量量化后图片:%d色' % num_vq, fontsize=20) plt.imshow(vq_image) # plt.savefig('2.png') plt.tight_layout(1.2) plt.show() Canopy聚类算法:簇中心点分布均匀、K值不需要指定、样本可以属于多个簇类和一次迭代,一般用于在K-Means算法之前获取先验知识即K的个数和簇中心分布位置 聚类算法评估指标: Given Label: 同一性(Homogeneity):一个簇中只包含一个类别样本 完整性(Completeness):同类别样本归属到同一个簇中 同一性与完整性TradeOff互相制约,两者加权平均的评估指标V-Measure: 轮廓系数: 度量样本与同簇其他样本的相似性:同簇中每个样本到同簇内其他样本的平均距离 度量样本与其他簇的不相似性:簇中每个样本到不同簇内所有样本的平均距离,与不同簇之间的最小平均距离 样本聚类合理Si接近1应该分到其他簇中Si接近-1在簇分界上Si接近0 from sklearn import metrics引入评估模块 if __name__ == "__main__": y = [0, 0, 0, 1, 1, 1] y_hat = [0, 0, 1, 1, 2, 2] h = metrics.homogeneity_score(y, y_hat)获取同一性评估指标 c = metrics.completeness_score(y, y_hat)获取完整性评估指标 print(u'同一性(Homogeneity):', h) print(u'完整性(Completeness):', c) v2 = 2 * c * h / (c + h) v = metrics.v_measure_score(y, y_hat)获取V-Measure评估指标 print(u'V-Measure:', v2, v) y = [0, 0, 0, 1, 1, 1] y_hat = [0, 0, 1, 3, 3, 3] h = metrics.homogeneity_score(y, y_hat) c = metrics.completeness_score(y, y_hat) v = metrics.v_measure_score(y, y_hat) print(u'同一性(Homogeneity):', h) print(u'完整性(Completeness):', c) print(u'V-Measure:', v) # 允许不同值 y = [0, 0, 0, 1, 1, 1] y_hat = [1, 1, 1, 0, 0, 0] h = metrics.homogeneity_score(y, y_hat) c = metrics.completeness_score(y, y_hat) v = metrics.v_measure_score(y, y_hat) print(u'同一性(Homogeneity):', h) print(u'完整性(Completeness):', c) print(u'V-Measure:', v) """ y = [0, 0, 1, 1] y_hat = [0, 1, 0, 1] ari = metrics.adjusted_rand_score(y, y_hat) print(ari) y = [0, 0, 0, 1, 1, 1] y_hat = [0, 0, 1, 1, 2, 2] ari = metrics.adjusted_rand_score(y, y_hat) print(ari) """ 层次聚类(适用于有层级关系的数据样本): 分裂的层次聚类(DIANA):将原始数据集不断的迭代分裂,计算每个子数据集中的相似性,根据相似性继续迭代分裂,将数据集分裂成多个类别 凝聚的层次聚类(AGNES):将数据集的每个样本不断迭代向上聚类后按层聚类直到聚成一个数据集 密度聚类:统计样本周边的密度,将密度给定一个阈值,不断的将样本添加到最近的簇中,可以进行对不规则数据样本的聚类即不类似圆形(适合K-Means算法)的数据,密度聚类计算复杂度大,可以通过索引来降低计算时间降低查找速度 DBSCAN(Density-Based Spatial Clustering of Applications with Noise)密度聚类算法:给定对象半径内的区域为对象领域,区域内样本个数超过阈值的对象为核心对象,核心对象到区域内的其他样本为核心密度可达,其他样本迭代规划对象半径区域,核心密度可达通过样本区域传递到其他样本为密度可达,一个样本密度可达的两个样本成为密度相连,最大密度相连构成的集合为簇,一个样本既不是核心对象也不能被别的样本密度可达为噪声 import numpy as np import matplotlib.pyplot as plt import sklearn.datasets as ds import matplotlib.colors from sklearn.cluster import DBSCAN from sklearn.preprocessing import StandardScaler def expand(a, b): d = (b - a) * 0.1 return a-d, b+d if __name__ == "__main__": N = 1000 centers = [[1, 2], [-1, -1], [1, -1], [-1, 1]] data, y = ds.make_blobs(N, n_features=2, centers=centers, cluster_std=[0.5, 0.25, 0.7, 0.5], random_state=0)生成模拟数据 data = StandardScaler().fit_transform(data)归一化先进行均值归一化后进行方差归一化 # 数据的参数:(epsilon, min_sample) params = ((0.2, 5), (0.2, 10), (0.2, 15), (0.3, 5), (0.3, 10), (0.3, 15)) matplotlib.rcParams['font.sans-serif'] = [u'SimHei'] matplotlib.rcParams['axes.unicode_minus'] = False plt.figure(figsize=(12, 8), facecolor='w') plt.suptitle(u'DBSCAN聚类', fontsize=20) for i in range(6): eps, min_samples = params[i] model = DBSCAN(eps=eps, min_samples=min_samples)获取DBSCAN聚类模型 model.fit(data) y_hat = model.labels_ core_indices = np.zeros_like(y_hat, dtype=bool) core_indices[model.core_sample_indices_] = True y_unique = np.unique(y_hat) n_clusters = y_unique.size - (1 if -1 in y_hat else 0) print(y_unique, '聚类簇的个数为:', n_clusters) plt.subplot(2, 3, i+1) clrs = plt.cm.Spectral(np.linspace(0, 0.8, y_unique.size)) print(clrs) for k, clr in zip(y_unique, clrs): cur = (y_hat == k) if k == -1: plt.scatter(data[cur, 0], data[cur, 1], s=20, c='k') continue plt.scatter(data[cur, 0], data[cur, 1], s=30, c=clr, edgecolors='k') plt.scatter(data[cur & core_indices][:, 0], data[cur & core_indices][:, 1], s=60, c=clr, marker='o', edgecolors='k') x1_min, x2_min = np.min(data, axis=0) x1_max, x2_max = np.max(data, axis=0) x1_min, x1_max = expand(x1_min, x1_max) x2_min, x2_max = expand(x2_min, x2_max) plt.xlim((x1_min, x1_max)) plt.ylim((x2_min, x2_max)) plt.grid(True) plt.title(u'epsilon = %.1f m = %d,聚类数目:%d' % (eps, min_samples, n_clusters), fontsize=16) plt.tight_layout() plt.subplots_adjust(top=0.9) plt.show() 谱和谱聚类: 谱:Y=A*X,矩阵X乘以A等于对矩阵X做了空间线性变换,那么Y=map(X),A是map这个线性算子,它的所有特征值的全体,称之为方阵的谱,方阵的谱半径为最大的特征值 谱聚类是一种基于图论的聚类方法,通过对样本数据的拉普拉斯矩阵的特征向量进行聚类,以达到对样本数据进行聚类的目的 谱聚类解决区域重叠问题,密度聚类与K-Means聚类不适合对区域重叠的数据进行聚类 样本数据集可以构建成全连接图,并且两两样本之间可以求相似度,两两样本之间构建邻接矩阵来表示图,邻接矩阵W上面的值是用高斯相似度计算 W矩阵按行或列加和得对角阵D L=D-W,L矩阵为Laplace矩阵 向量v与变换A满足Av=λv,向量v是变换A的一个特征向量,λ是相应的特征值 L矩阵是N*N的,N是样本个数,实数形成的对数矩阵,求特征值和特征向量 所有特征向量根据排序默认从小到大,逆序之后获取特征向量最大的几个列向量实现降维,用这些列向量表示新的对应每个样本的重要特征,然后用K-Means聚类算法对样本进行聚类即Laplace矩阵做主成分分析PCA(主成分分析技术,又称主分量分析,利用降维的思想将多指标转化为少数几个综合指标)进行做K均值聚类 import numpy as np import matplotlib.pyplot as plt import matplotlib.colors from sklearn.cluster import spectral_clustering from sklearn.metrics import euclidean_distances def expand(a, b): d = (b - a) * 0.1 return a-d, b+d if __name__ == "__main__": matplotlib.rcParams['font.sans-serif'] = [u'SimHei'] matplotlib.rcParams['axes.unicode_minus'] = False t = np.arange(0, 2*np.pi, 0.1) data1 = np.vstack((np.cos(t), np.sin(t))).T data2 = np.vstack((2*np.cos(t), 2*np.sin(t))).T data3 = np.vstack((3*np.cos(t), 3*np.sin(t))).T data = np.vstack((data1, data2, data3)) n_clusters = 3 m = euclidean_distances(data, squared=True) sigma = np.median(m) plt.figure(figsize=(12, 8), facecolor='w') plt.suptitle(u'谱聚类', fontsize=20) clrs = plt.cm.Spectral(np.linspace(0, 0.8, n_clusters)) for i, s in enumerate(np.logspace(-2, 0, 6)): print(s) af = np.exp(-m ** 2 / (s ** 2)) + 1e-6 y_hat = spectral_clustering(af, n_clusters=n_clusters, assign_labels='kmeans', random_state=1) plt.subplot(2, 3, i+1) for k, clr in enumerate(clrs): cur = (y_hat == k) plt.scatter(data[cur, 0], data[cur, 1], s=40, c=clr, edgecolors='k') x1_min, x2_min = np.min(data, axis=0) x1_max, x2_max = np.max(data, axis=0) x1_min, x1_max = expand(x1_min, x1_max) x2_min, x2_max = expand(x2_min, x2_max) plt.xlim((x1_min, x1_max)) plt.ylim((x2_min, x2_max)) plt.grid(True) plt.title(u'sigma = %.2f' % s, fontsize=16) plt.tight_layout() plt.subplots_adjust(top=0.9) plt.show() TensorFlow是Google Brain 2015年11月在GitHub开源 TensorFlow官方网址:www.tensorflow.org GitHub网址:https://github.com/tensorflow/tensorflow 模型仓库网址:https://github.com/tensorflow/models TensorFlow支持的语言Python、C++、GO、Java,后端语言C++、CUDA(Compute Unified Device Architecture,可以在GPU上执行的语言,需要GPU显卡品牌为NVIDIA) TensorFlow实现的算法可以在其他异构的系统上方便的移植,比如普通CPU服务器、GPU集群、Android、IPhone TensorFlow不仅可以执行深度学习算法,还可以用来实现其他算法,包括线性回归、逻辑回归、随 机森林等 TensorFlow建立的大规模深度学习模型应用场景非常广,包括语音识别、自然语言处理、计算机 视觉、机器人控制、信息抽取、药物研发、分子活动预测 为了研究超大规模的深度神经网络,Google在2011年启动了Google Brain项目,比如Google Search中的搜索结果排序、Google Photos中的图片标注、Google Translate中的自然语言处理,都依赖建立的深度学习模型,2016年已经有超过2000个项目使用了TensorFlow建立的深度学习模型 TensorFlow中的计算可以表示为一个有向图(Directed Graph)或者称计算图(Computation Graph),其中每一个运算操作(operation)将作为一个节点(node),计算图描述了数据的计算流程,也负责维护和更新状态,用户通过python,c++,go,Java语言设计这个这个数据计算的有向图,计算图中每一个节点可以有任意多个输入和任意多个输出,每一个节点描述了一种运算操作,节点可以算是运算操作的实例化(instance),计算图中的边里面流动(flow)的数据被称为张量(tensor),故得名TensorFlow 有向无环图相关算法:CNN(卷积神级网络)、ANN(人工神经网络)、DNN(深度神经网络) 有向有环图相关算法:RNN(循环神经网络) pip install –upgrade --user tensorflow==版本号 以更新依赖包管理员身份安装TensorFlow tensorflow.__version__获取TensorFlow版本 tf.Variable生成变量节点 tf.device指定运行每一个操作的设备(本地CPU/GPU或远程服务器),每一个可用设备有相应的名称比如CPU在TensorFlow中的名称为/cpu:0,默认情况下不区分多个CPU名称所有CPU都使用/cpu:0作为名称,GPU名称/gpu:n(序列号n从0开始) 设置log_device_placement参数可以在生成会话时打印运行每一个运算的设备和运算的操作 TensorFlow默认优先选择GPU import tensorflow as tf with tf.device('/cpu:0'):使用Python的上下文管理器,with内部上下文对象为同一个 x = tf.Variable(3, name='x') y = tf.Variable(4, name='y') f = x*x*y + y + 2 sess = tf.Session(config=tf.ConfigProto(log_device_placement=True)) 创建一个配置为打印具体运行过程的计算图上下文环境 sess.run(x.initializer)初始化x,run函数立刻调用进行计算执行 sess.run(y.initializer) result = sess.run(f) print(result) sess.close() 使用Python的上下文管理器,指定with内部语句上下文对象为同一个计算图上下文环境对象tensorflow.Session import tensorflow as tf x = tf.Variable(3, name='x') y = tf.Variable(4, name='y') f = x*x*y + y + 2 init = tf.global_variables_initializer()定义全局所有变量初始化对象,定义逻辑操作不立即执行初始化 with tf.Session() as sess:使用Python的上下文管理器,with内部上下文对象为同一个tensorflow.Session x.initializer.run() # 等价于 tf.get_default_session().run(x.initializer) y.initializer.run() init.run()执行全局所有变量初始化 result = f.eval() # 等价于 tf.get_default_session().run(f) print(result) sess = tf.InteractiveSession()定义默认上下文环境对象session不需要使用Python的with语句体,但需要程序手动进行关闭tensorflow.Session sess.close()关闭tensorflow.Session TensorFlow程序会分为两部分,第一部分是构建阶段(创建计算图,通常建立表示机器学习模型的的计算图,和需要去训练模型的计算图),第二部分是执行阶段(通常运行Loop循环重复训练步骤,每一步训练小批量数据,逐渐的改进模型参数) import tensorflow as tf # 任何创建的节点会自动加入到默认的图 x1 = tf.Variable(1) print(x1.graph is tf.get_default_graph()) 获取变量节点是否为Tensorflow默认图,创建的节点会加入到默认图中年 graph = tf.Graph()自定义图 x3 = tf.Variable(3) with graph.as_default():需要使用Python的with修改上下文环境改变Tensorflow默认图作用域即当前图为自定义图 x2 = tf.Variable(2) print(x2.graph is graph) print(x2.graph is tf.get_default_graph()) print(x3.graph is tf.get_default_graph()) TensorFlow计算一个节点的时会自动先进行其依赖节点的计算,TensorFlow只对Variable值进行缓存,Variable的生命周期是initializer运行开始到会话session close结束 import tensorflow as tf # 当去 w = tf.constant(3) x = w + 2 y = x + 5 z = x * 3 with tf.Session() as sess: print(y.eval())计算y和z在同一个会话中但不在同一个图中w和x逻辑会被多次执行 print(z.eval()) with tf.Session() as sess: y_val, z_val = sess.run([y, z])计算y和z在同一个图中不会重复计算w和x逻辑 print(y_val) print(z_val) TensorFlow的解析解多元线性回归: import tensorflow as tf引入TensorFlow模块 import numpy as np from sklearn.datasets import fetch_california_housing引入加利福尼亚房价数据集 housing = fetch_california_housing(data_home="C:/Users/28542/scikit_learn_data", download_if_missing=False)获取数据集,无论是否已存在都下载数据集 m, n = housing.data.shape获取获得数据行数和列数 housing_data_plus_bias = np.c_[np.ones((m, 1)), housing.data]使用numpy会立即执行添加一个额外的bias输入特征(x0=1)到所有的训练数据上面 X = tf.constant(housing_data_plus_bias, dtype=tf.float32, name='X')创建持有数据和标签名的TensorFlow常量节点,不进行缓存计算到常量节点都会重新使用逻辑赋值常量 y = tf.constant(housing.target.reshape(-1, 1), dtype=tf.float32, name='y') XT = tf.transpose(X)获取矩阵X的转置矩阵 theta = tf.matmul(tf.matmul(tf.matrix_inverse(tf.matmul(XT, X)), XT), y) 解析解计算出最优解,matmul矩阵的点积,matrix_inverse矩阵的逆 with tf.Session() as sess: theta_value = theta.eval() # sess.run(theta) print(theta_value) TensorFlow实现梯度下降线性回归 import tensorflow as tf import numpy as np from sklearn.datasets import fetch_california_housing from sklearn.preprocessing import StandardScaler n_epochs = 1000 learning_rate = 0.01 # BGD = Batch Gradient Decrease如果面向数据集比较大时可以使用Mini GD housing = fetch_california_housing() m, n = housing.data.shape housing_data_plus_bias = np.c_[np.ones((m, 1)), housing.data] scaler = StandardScaler().fit(housing_data_plus_bias)获取归一化对象 scaled_housing_data_plus_bias = scaler.transform(housing_data_plus_bias)获取归一化结果 X = tf.constant(scaled_housing_data_plus_bias, dtype=tf.float32, name='X') y = tf.constant(housing.target.reshape(-1, 1), dtype=tf.float32, name='y') # random_uniform函数创建图里一个节点包含随机数值,给定它的形状和取值范围,就像numpy里面rand()函数 theta = tf.Variable(tf.random_uniform([n + 1, 1], -1.0, 1.0), name='theta')初始化theta为一列n+1个在[-1,1]的值 y_pred = tf.matmul(X, theta, name="predictions")使用TensorFlow的梯度计算 error = y_pred - y mse = tf.reduce_mean(tf.square(error), name="mse") # 梯度的公式:(y_pred - y) * xj # gradients = 2/m * tf.matmul(tf.transpose(X), error)自定义梯度下降公式 # gradients = tf.gradients(mse, [theta])[0]使用TensorFlow求梯度方式 # 赋值函数对于BGD来说就是 theta_new = theta - (learning_rate * gradients)自定义梯度下降 # training_op = tf.assign(theta, theta - learning_rate * gradients)使用TensorFlow的重新赋值封装方法梯度下降 optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)使用TensorFlow优化器进行计算梯度以及梯度下降 # MomentumOptimizer收敛会比梯度下降更快 # optimizer = tf.train.MomentumOptimizer(learning_rate=learning_rate, momentum=0.9) training_op = optimizer.minimize(mse)使用优化器找到损失函数最小值 init = tf.global_variables_initializer() A = tf.placeholder(tf.float32, shape=(None, 3)) TensorFlow创建占位符节点,指定数据类型和数据形状(None不确定大小任意数量)无默认值的变量 B = A + 5 # 下面是开始训练 with tf.Session() as sess: sess.run(init) for epoch in range(n_epochs): if epoch % 100 == 0: print("Epoch", epoch, "MSE = ", mse.eval()) sess.run(training_op) best_theta = theta.eval() print(best_theta) B_val_1 = B.eval(feed_dict={A: [[1, 2, 3]]})计算节点需要将依赖的占位符节点指定数据 TensorFlow实现Softmax回归: from tensorflow.examples.tutorials.mnist import input_data引入MNIST数据集模块 import tensorflow as tf my_mnist = input_data.read_data_sets("MNIST_data_bak/", one_hot=True)读取进行one_hot编码后的数据集 # 输入的是一堆图片,None表示不限输入条数,784表示每张图片都是一个784个像素值的一维向量 # 所以输入的矩阵是None乘以784二维矩阵 x = tf.placeholder(dtype=tf.float32, shape=(None, 784)) # 初始化都是0,二维矩阵784乘以10个W值 W = tf.Variable(tf.zeros([784, 10])) b = tf.Variable(tf.zeros([10])) y = tf.nn.softmax(tf.matmul(x, W) + b)使用TensorFlowSoftmax回归算法定义计算图逻辑 # 训练 # labels是每张图片都对应一个one-hot的10个值的向量 y_ = tf.placeholder(dtype=tf.float32, shape=(None, 10)) # 定义损失函数,交叉熵损失函数 # 对于多分类问题,通常使用交叉熵损失函数 # reduction_indices等价于axis,指明按照每行加,还是按照每列加 cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))定义损失函数交叉熵的计算逻辑 train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)使用TensorFlow优化器进行梯度下降找最优解 # 评估 # tf.argmax()是一个从tensor中寻找最大值的序号,tf.argmax就是求各个预测的数字中概率最大的那一个 correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1)) # 用tf.cast将之前correct_prediction输出的bool值转换为float32,再求平均 accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) # 初始化变量 sess = tf.InteractiveSession() tf.global_variables_initializer().run() for _ in range(1000): batch_xs, batch_ys = my_mnist.train.next_batch(100) sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys}) print("TrainSet batch acc : %s " % accuracy.eval({x: batch_xs, y_: batch_ys})) print("ValidSet acc : %s" % accuracy.eval({x: my_mnist.validation.images, y_: my_mnist.validation.labels})) # 测试 print("TestSet acc : %s" % accuracy.eval({x: my_mnist.test.images, y_: my_mnist.test.labels})) TensorFlow保存变量和模型以及加载模型: from tensorflow.examples.tutorials.mnist import input_data import tensorflow as tf my_mnist = input_data.read_data_sets("MNIST_data_bak/", one_hot=True) x = tf.placeholder(dtype=tf.float32, shape=(None, 784)) W = tf.Variable(tf.zeros([784, 10])) b = tf.Variable(tf.zeros([10])) y = tf.nn.softmax(tf.matmul(x, W) + b) y_ = tf.placeholder(dtype=tf.float32, shape=(None, 10)) cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1])) train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy) init = tf.global_variables_initializer() saver = tf.train.Saver()创建TensorFlow保存节点Saver,一般在构建计算图完成后 n_epoch = 1000 with tf.Session() as sess: sess.run(init) for epoch in range(n_epoch): if epoch % 100 == 0: save_path = saver.save(sess, "./ckpt/my_model.ckpt")保存节点Saver保存中间模型数据到指定路径即checkpoint检查点 batch_xs, batch_ys = my_mnist.train.next_batch(100) sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys}) best_theta = W.eval() save_path = saver.save(sess, "./ckpt/my_model_final.ckpt")保存节点Saver保存指定模型数据到指定路径 saver.restore(sess, "./ckpt/my_model_final.ckpt")保存节点恢复指定路径数据到模型会话 correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) print(accuracy.eval({x: my_mnist.test.images, y_: my_mnist.test.labels})) 模块化封装: import tensorflow as tf def relu(X):定义函数模块化封装变量 w_shape = (int(X.get_shape()[1]), 1) w = tf.Variable(tf.random_uniform(w_shape), name='weights') b = tf.Variable(0.0, name='bias') z = tf.add(tf.matmul(X, w), b, name='z') return tf.maximum(z, 0., name='relu') n_features = 3 X = tf.placeholder(tf.float32, shape=(None, n_features), name='X') relus = [relu(X) for i in range(5)] output = tf.add_n(relus, name='output')多个值进行相加和 init = tf.global_variables_initializer() with tf.Session() as sess: sess.run(init) result = output.eval(feed_dict={X: [[1, 2, 3], [4, 5, 6], [7, 8, 9]]}) print(result) ANN人工神经网络除输出层每层神经元包括bias(权重W0)全连接下一层神经元,其中有一个隐藏层一般称为多层感知机,有两个或两个以上隐藏层称为DNN深度神经网络, import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data import numpy as np from tensorflow.contrib.layers import fully_connected # 构建图阶段 n_inputs = 28*28 n_hidden1 = 300 n_hidden2 = 100 n_outputs = 10 X = tf.placeholder(tf.float32, shape=(None, n_inputs), name='X') y = tf.placeholder(tf.int64, shape=(None), name='y') # 构建神经网络层 def neuron_layer(X, n_neurons, name, activation=None):输出层可以看做是激活函数为Softmax的隐藏层 with tf.name_scope(name):名称范围便于区分 n_inputs = int(X.get_shape()[1])获取输入层的维度作为层的输入连接个数 stddev = 2 / np.sqrt(n_inputs)初始化权重W的方差,标准方差可以让收敛快 init = tf.truncated_normal((n_inputs, n_neurons), stddev=stddev)初始化权重W参数矩阵truncated normal distribution比regular normal distribution的值小可以慢慢的稳健的训练,W的初始化参数需要随机,不能为0,否则输出为0,最后调整都是一个幅度没意义 w = tf.Variable(init, name='weights') b = tf.Variable(tf.zeros([n_neurons]), name='biases')定义W0参数为0 z = tf.matmul(X, w) + b if activation == "relu":选择激活函数 return tf.nn.relu(z) else: return z with tf.name_scope("dnn"): hidden1 = neuron_layer(X, n_hidden1, "hidden1", activation="relu")定义隐藏层 hidden2 = neuron_layer(hidden1, n_hidden2, "hidden2", activation="relu") # 进入到softmax之前的结果 logits = neuron_layer(hidden2, n_outputs, "outputs")定义输出层 # with tf.name_scope("dnn"):TensorFlow封装的初始化w和b的策略,默认使用relu激活函数 # hidden1 = fully_connected(X, n_hidden1, scope="hidden1") # hidden2 = fully_connected(hidden1, n_hidden2, scope="hidden2") # logits = fully_connected(hidden2, n_outputs, scope="outputs", activation_fn=None) with tf.name_scope("loss"):定义交叉熵损失函数,并且求个样本平均 xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits) 函数等价于先使用softmax损失函数,再接着计算交叉熵,并且更有效率,sparse_softmax_cross_entropy_with_logits函数对分类号labels进行处理,softmax_cross_entropy_with_logits函数对one-hot编码labels进行处理 loss = tf.reduce_mean(xentropy, name="loss") learning_rate = 0.01 with tf.name_scope("train"): optimizer = tf.train.GradientDescentOptimizer(learning_rate)定义梯度下降优化器 training_op = optimizer.minimize(loss)找到最小损失函数值 with tf.name_scope("eval"): correct = tf.nn.in_top_k(logits, y, 1)获取logits最大的第一个值的索引与y比较是否相等 accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))获取将True和False强制转换为1和0并相加和求平均 init = tf.global_variables_initializer() saver = tf.train.Saver() # 计算图阶段 mnist = input_data.read_data_sets("MNIST_data_bak/") n_epochs = 400 batch_size = 50 with tf.Session() as sess: init.run() for epoch in range(n_epochs): for iteration in range(mnist.train.num_examples // batch_size):训练整个训练集 X_batch, y_batch = mnist.train.next_batch(batch_size) sess.run(training_op, feed_dict={X: X_batch, y: y_batch})每次训练小批量数据 acc_train = accuracy.eval(feed_dict={X: X_batch, y: y_batch})获取小批量数据的正确率 acc_test = accuracy.eval(feed_dict={X: mnist.test.images, y: mnist.test.labels})获取测试集的正确率 print(epoch, "Train accuracy:", acc_train, "Test accuracy:", acc_test) save_path = saver.save(sess, "./my_dnn_model_final.ckpt") ''' # 使用模型预测 with tf.Session as sess: saver.restore(sess, "./my_dnn_model_final.ckpt") X_new_scaled = [...] Z = logits.eval(feed_dict={X: X_new_scaled}) y_pred = np.argmax(Z, axis=1) # 查看最大的类别是哪个 ''' TensorBoard可视化: import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data max_steps = 1000 learning_rate = 0.001 dropout = 0.9 data_dir = './MNIST_data_bak' log_dir = './logs/mnist_with_summaries' mnist = input_data.read_data_sets(data_dir, one_hot=True) sess = tf.InteractiveSession()启动上下文会话对象 with tf.name_scope('input'): x = tf.placeholder(tf.float32, [None, 784], name='x-input') y_ = tf.placeholder(tf.float32, [None, 10], name='y-input') with tf.name_scope('input_reshape'): image_shaped_input = tf.reshape(x, [-1, 28, 28, 1])将X矩阵转换为图片对象节点,-1即不确定图片的数量、28,28图片的高和宽,1图片的颜色通道 tf.summary.image('input', image_shaped_input, 10)保存总结信息,TensorFlow将转换后的图片对象信息保存10个到TensorFlow的图片总结信息中,区域为input # 定义神经网络的初始化方法 def weight_variable(shape):定义权重W initial = tf.truncated_normal(shape, stddev=0.1) return tf.Variable(initial) def bias_variable(shape):定义截距b即W0 initial = tf.constant(0.1, shape=shape) return tf.Variable(initial) def variable_summaries(var): 定义Variable变量的数据汇总函数,计算出变量的mean、stddev、max、min等标量数据信息保存到TensorFlow.summary.scalar进行记录和汇总 with tf.name_scope('summaries'): mean = tf.reduce_mean(var) tf.summary.scalar('mean', mean) with tf.name_scope('stddev'): stddev = tf.sqrt(tf.reduce_mean(tf.square(var - mean))) tf.summary.scalar('stddev', stddev) tf.summary.scalar('max', tf.reduce_max(var)) tf.summary.scalar('min', tf.reduce_min(var)) tf.summary.histogram('histogram', var) 记录变量var的直方图数据 def nn_layer(input_tensor, input_dim, output_dim, layer_name, act=tf.nn.relu):定义MLP多层神经网络来训练数据,每一层中都对模型数据进行汇总 with tf.name_scope(layer_name): with tf.name_scope('weights'): weights = weight_variable([input_dim, output_dim]) variable_summaries(weights) with tf.name_scope('biases'): biases = bias_variable([output_dim]) variable_summaries(biases) with tf.name_scope('Wx_plus_b'): preactivate = tf.matmul(input_tensor, weights) + biases tf.summary.histogram('pre_activations', preactivate) activations = act(preactivate, name='activation') tf.summary.histogram('activations', activations) return activations # 我们使用刚刚定义的函数创建一层神经网络,输入维度是图片的尺寸784=28*28 # 输出的维度是隐藏节点数500,再创建一个Dropout层,并使用tf.summary.scalar记录keep_prob # 然后使用nn_layer定义神经网络输出层,其输入维度为上一层隐含节点数500,输出维度为类别数10 # 同时激活函数为全等映射identity,暂时不使用softmax hidden1 = nn_layer(x, 784, 500, 'layer1') with tf.name_scope('dropout'): keep_prob = tf.placeholder(tf.float32) tf.summary.scalar('dropout_keep_probability', keep_prob) dropped = tf.nn.dropout(hidden1, keep_prob) y = nn_layer(dropped, 500, 10, 'layer2', act=tf.identity) with tf.name_scope('cross_entropy'): diff = tf.nn.softmax_cross_entropy_with_logits(logits=y, labels=y_)对输出层的结果进行Softmax with tf.name_scope('total'): cross_entropy = tf.reduce_mean(diff) 处理并计算交叉熵损失cross_entropy,计算平均的损失 tf.summary.scalar('cross_entropy', cross_entropy) with tf.name_scope('train'): train_step = tf.train.AdamOptimizer(learning_rate).minimize(cross_entropy) 使用Adam优化器对损失进行优化 with tf.name_scope('accuracy'): with tf.name_scope('correct_prediction'): correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1)) with tf.name_scope('accuracy'): accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) tf.summary.scalar('accuracy', accuracy) merged = tf.summary.merge_all()获取所有汇总操作即tf.summary,以便后面执行 # 定义两个tf.summary.FileWriter文件记录器再不同的子目录,分别用来存储训练和测试的日志数据 train_writer = tf.summary.FileWriter(log_dir + '/train', sess.graph)定义文件记录器保存训练的日志数据,将Session计算图sess.graph加入训练过程,在TensorBoard的GRAPHS窗口中可以展示 test_writer = tf.summary.FileWriter(log_dir + '/test') 定义文件记录器保存测试的日志数据 tf.global_variables_initializer().run()初始化全部变量 # 定义feed_dict函数,如果是训练,需要设置dropout,如果是测试,keep_prob设置为1 def feed_dict(train): if train: xs, ys = mnist.train.next_batch(100) k = dropout else: xs, ys = mnist.test.images, mnist.test.labels k = 1.0 return {x: xs, y_: ys, keep_prob: k} # 执行训练、测试、日志记录操作 # 创建模型的保存器 saver = tf.train.Saver() for i in range(max_steps): if i % 10 == 0: summary, acc = sess.run([merged, accuracy], feed_dict=feed_dict(False)) test_writer.add_summary(summary, i) print('Accuracy at step %s: %s' % (i, acc)) else: if i % 100 == 99: run_options = tf.RunOptions(trace_level=tf.RunOptions.FULL_TRACE) run_metadata = tf.RunMetadata() summary, _ = sess.run([merged, train_step], feed_dict=feed_dict(True)) train_writer.add_run_metadata(run_metadata, 'step%03d' % i) train_writer.add_summary(summary, 1) saver.save(sess, log_dir + 'model.ckpt', i) print('Adding run metadata for', i) else: summary, _ = sess.run([merged, train_step], feed_dict=feed_dict(True)) train_writer.add_summary(summary, i) train_writer.close()关闭文件流 test_writer.close() tensorboard --logdir "日志目录" 启动对应日志目录的TensorBoard可视化界面,TensorBoard读取指定日志目录将保存的数据信息进行展示 TensorBoard可视化界面地址:http://主机名:6006 卷积神经网络CNN中重要的构建单元卷积层:神经元在每个卷积层不是将图片转换为一维将所有像素作为输入而是将图片像素进行归纳汇总成感受野的像素作为输入即卷积层每层之间的神经元不是全连接 每层卷积层将上一层的图片像素按照指定方块大小(卷积核)进行特征抽取归纳总结(卷积)形成新的图片像素传递给下一层,最后一层卷积层的结果输入给FC全连接隐藏层进行分析 卷积的计算方式: Filter卷积核(Convolution Kernels)矩阵中的每个位置与图片映射的对应位置进行相乘后相加和作为卷积后的值,卷积核按照指定的Stride(步长)进行相应移动计算下一个卷积值,所有卷积值组成卷积特征提取的结果矩阵特征图(Feature Map) D为深度,F为Filter的大小(宽度或高度),Wdmn为Filter的第m行第n列权重,adij为图像第d层i行j列像素 Filter卷积核中中间列为1其他列为0即卷积核矩阵只有中间一列为1称为垂直线滤波器(Vertical line filter),中间行为1其他行为0即卷积核矩阵只有中间一行为1称为水平线滤波器(Horizontal line filter),不同的卷积核相当于在不同的角度或视角审视图片 步长为1进行卷积时可以进行填充(Padding)得到与源图片矩阵大小一样的特征图,一般填充为0(Zero Padding),填充后卷积以卷积核中心对应位置计算,Padding模式valid不使用Zero Padding可能忽略图像的右侧或底下,same必须使用Zero Padding输出神经元个数等于输入神经元个数除以步长向上取整 import numpy as np from sklearn.datasets import load_sample_images import tensorflow as tf import matplotlib.pyplot as plt # 加载数据集 # 输入图片通常是3D,[height, width, channels] # mini-batch通常是4D,[mini-batch size, height, width, channels] dataset = np.array(load_sample_images().images, dtype=np.float32) # 数据集里面两张图片,一个中国庙宇,一个花 batch_size, height, width, channels = dataset.shape获取数据集形状属性,数据量、高、宽、通道3即RGB print(batch_size, height, width, channels) # 创建两个filter # 高,宽,通道,卷积核 # 7, 7, channels, 2 filters_test = np.zeros(shape=(7, 7, channels, 2), dtype=np.float32)定义卷积核矩阵 filters_test[:, 3, :, 0] = 1定义垂直线滤波器卷积核矩阵 filters_test[3, :, :, 1] = 1定义水平线滤波器卷积核矩阵 # filter参数是一个filters的集合 X = tf.placeholder(tf.float32, shape=(None, height, width, channels)) # strides=[1, 2, 2, 1] 中第一最后一个为1,中间对应sh和sw convolution = tf.nn.conv2d(X, filter=filters_test, strides=[1, 2, 2, 1], padding='SAME')使用TensorFlow定义对图片进行二维卷积(文本一维,图片二维,视频三维)计算逻辑 with tf.Session() as sess: output = sess.run(convolution, feed_dict={X: dataset}) plt.imshow(load_sample_images().images[0]) # 绘制源图片 plt.show() plt.imshow(output[0, :, :, 0]) # 绘制第一个图的第二个特征图 plt.show() 池化Pooling:降采样subsample,和shrink,减少计算负荷和内存使用,参数数量(也可防止过拟合),减少输入图片大小可以使神经网络可以经受图片平移,不受位置的影响,与卷积神经网络类似,在池化层中的每个神经元不是被全连接连接到上面一层输出的神经元,只对应一小块感受野的区域,池化神经元没有权重值即权重值一致全为1,是聚合输入根据取最大或者是求均值向下传递,其他输入值被忽略丢弃,池化Pooling模式使用Padding的valid import numpy as np from sklearn.datasets import load_sample_images import tensorflow as tf import matplotlib.pyplot as plt # 加载数据集 # 输入图片通常是3D,[height, width, channels] # mini-batch通常是4D,[mini-batch size, height, width, channels] dataset = np.array(load_sample_images().images, dtype=np.float32) # 数据集里面两张图片,一个中国庙宇,一个花 batch_size, height, width, channels = dataset.shape print(batch_size, height, width, channels) # 创建输入和一个池化层 X = tf.placeholder(tf.float32, shape=(None, height, width, channels)) # TensorFlow不支持池化多个实例,所以ksize的第一个batch size是1 # TensorFlow不支持池化同时发生的长宽高,所以必须有一个是1,这里channels就是depth维度为1 max_pool = tf.nn.max_pool(X, ksize=[1, 4, 4, 1], strides=[1, 4, 4, 1], padding='VALID') # avg_pool() with tf.Session() as sess: output = sess.run(max_pool, feed_dict={X: dataset}) plt.imshow(output[0].astype(np.uint8)) # 画输入的第一个图像 plt.show() 典型的CNN架构:图像先进行多层卷积层(每个卷积层后一个接relu层和一个池化层)处理后输入给全连接神经网络层和relu层最后是输出层Softmax层输出预测的类概率,卷积层的卷积核过大会增加权重值的计算量卷积后的结果与小卷积核结果可能一致 图像模型评估:top-five错误率是测试图片系统判断前5个类别预测都没有包含正确答案的数量,由于CNN模型的出现,错误率从26%降到了3% 经典模型:LeNet-5架构(1998年)、AlexNet(2012年)、GoogLeNet(2014年,加深层次)、ResNet(2015年,层次循环) LeNet-5架构:最知名的CNN架构,Yann LeCun在1998年创建,用于MNIST手写体识别 使用均值池化,C3层没有全连接C2池化层,最后一层使用欧拉距离测量输入向量和对应权值向量距离(一般用交叉熵,惩罚错误的预测) Dropout:在深度学习中,防止过拟合最常用的正则化技术,即使在顶尖水准的神经网络中也可以带来1%到2%的准确度提升,如果模型已经有了95%的准确率,获得2%的准确率提升意味着降低错误率大概40%,即从5%的错误率降低到3%的错误率,在每一次训练step中,每个神经元包括输入神经元不包括输出神经元有一个概率被临时的丢掉即将被忽视在整个这次训练step中,有可能下次再被激活,超参数p为dropout rate即神经元被忽略的概率,一般设置50%,训练完成后的模型不进行dropout import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data mnist = input_data.read_data_sets('MNIST_data_bak/', one_hot=True) sess = tf.InteractiveSession() def weight_variable(shape):初始化权重值标准差为0.1避免死亡节点(dead neurons)即权重值为0 initial = tf.truncated_normal(shape, stddev=0.1) return tf.Variable(initial) def bias_variable(shape): 初始化截距的正太分布噪声标准差为0.1 initial = tf.constant(0.1, shape=shape) return tf.Variable(initial) # 卷积层和池化层也是接下来要重复使用的,因此也为它们定义创建函数 # tf.nn.conv2d是TensorFlow中的2维卷积函数,参数中x是输入,W是卷积的参数,比如[5, 5, 1, 32] # 前面两个数字代表卷积核的尺寸,第三个数字代表有多少个channel,因为我们只有灰度单色,所以是1,如果是彩色的RGB图片,这里是3 # 最后代表核的数量,也就是这个卷积层会提取多少类的特征 # Strides代表卷积模板移动的步长,都是1代表会不遗漏地划过图片的每一个点!Padding代表边界的处理方式,这里的SAME代表给 # 边界加上Padding让卷积的输出和输入保持同样SAME的尺寸 def conv2d(x, W): return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME') # tf.nn.max_pool是TensorFlow中的最大池化函数,我们这里使用2*2的最大池化,即将2*2的像素块降为1*1的像素 # 最大池化会保留原始像素块中灰度值最高的那一个像素,即保留最显著的特征,因为希望整体上缩小图片尺寸,因此池化层 # strides也设为横竖两个方向以2为步长。如果步长还是1,那么我们会得到一个尺寸不变的图片 def max_pool_2x2(x): return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME') # 因为卷积神经网络会利用到空间结构信息,因此需要将1D的输入向量转为2D的图片结构,即从1*784的形式转为原始的28*28的结构 # 同时因为只有一个颜色通道,故最终尺寸为[-1, 28, 28, 1],前面的-1代表样本数量不固定,最后的1代表颜色通道数量 x = tf.placeholder(tf.float32, [None, 784]) y_ = tf.placeholder(tf.float32, [None, 10]) x_image = tf.reshape(x, [-1, 28, 28, 1]) # 定义我的第一个卷积层,我们先使用前面写好的函数进行参数初始化,包括weights和bias,这里的[5, 5, 1, 32]代表卷积 # 核尺寸为5*5,1个颜色通道,32个不同的卷积核,然后使用conv2d函数进行卷积操作,并加上偏置项,接着再使用ReLU激活函数进行 # 非线性处理,最后,使用最大池化函数max_pool_2*2对卷积的输出结果进行池化操作 W_conv1 = weight_variable([5, 5, 1, 32]) b_conv1 = bias_variable([32]) h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1) h_pool1 = max_pool_2x2(h_conv1) # 第二层和第一个一样,但是卷积核变成了64 W_conv2 = weight_variable([5, 5, 32, 64]) b_conv2 = bias_variable([64]) h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2) h_pool2 = max_pool_2x2(h_conv2) # 因为前面经历了两次步长为2*2的最大池化,所以边长已经只有1/4了,图片尺寸由28*28变成了7*7 # 而第二个卷积层的卷积核数量为64,其输出的tensor尺寸即为7*7*64 # 我们使用tf.reshape函数对第二个卷积层的输出tensor进行变形,将其转成1D的向量 # 然后连接一个全连接层,隐含节点为1024,并使用ReLU激活函数 W_fc1 = weight_variable([7 * 7 * 64, 1024]) b_fc1 = bias_variable([1024]) h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 64]) h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1) # 防止过拟合,使用Dropout层 keep_prob = tf.placeholder(tf.float32) h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob) # 接 Softmax分类 W_fc2 = weight_variable([1024, 10]) b_fc2 = bias_variable([10]) y_conv = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2) # 定义损失函数 cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y_conv), reduction_indices=[1])) train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy) correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) # 训练 tf.global_variables_initializer().run() for i in range(20000): batch = mnist.train.next_batch(50) if i % 100 == 0: train_accuracy = accuracy.eval(feed_dict={x: batch[0], y_: batch[1], keep_prob: 1.0}) print("step %d, training accuracy %g" % (i, train_accuracy)) train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5}) print("test accuracy %g" % accuracy.eval(feed_dict={ x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0 })) # 最后,这个CNN模型可以得到的准确率约为99.2%,基本可以满足对手写数字识别准确率的要求 # 相比之前的MLP的2%的错误率,CNN的错误率下降了大约60%,这里主要的性能提升都来自于更优秀的网络设计 # 即卷积网络对图像特征的提取和抽象能力,依靠卷积核的权值共享,CNN的参数数量并没有爆炸,降低计算量的同时 # 也减轻了过拟合,因此整个模型的性能有较大的提升,这里我们只是实现了一个简单的卷积神经网络,没有复杂的Trick 数据增大:从现有的数据产生一些新的训练样本,人工增大训练集减少过拟合,可以将图像轻微的平移、旋转、改变大小、然后增加这些变化后的图片到训练集,训练的模型可以经受位置、方向、大小的影响,用不同的对比度产生图像,训练的模型可以经受光条件的影响 TensorFlow提供一些图片操作算子,如Transposing(shifting),rotating, resizing, flipping cropping, adjusting brightness,contrast saturation hue 复杂的卷积网络MNIST数据集不适合用来评测其性能,一般使用CIFAR-10数据集进行训练 import tensorflow as tf import numpy as np import math import time from tutorials.image.cifar10 import cifar10 from tutorials.image.cifar10 import cifar10_input # 本节使用的数据集是CIFAR-10,这是一个经典的数据集,包含60000张32*32的彩色图像,其中训练集50000张,测试集10000张 # 一共标注为10类,每一类图片6000张。10类分别是 airplane, automobile, bird, cat, deer, dog, frog, horse, ship, truck # 我们载入一些常用库,比如NumPy和time,并载入TensorFlow Models中自动下载、读取CIFAR-10数据的类 max_steps = 3000 batch_size = 128 # 下载cifar10数据集的默认路径 data_dir = 'D:/PyCharm 2019.1.1/PythonStudy/AIStudy/tensorFlowStudy' def variable_with_weight_losses(shape, stddev, wl): # 定义初始化weights的函数,和之前一样依然使用tf.truncated_normal截断的正太分布来初始化权值 var = tf.Variable(tf.truncated_normal(shape, stddev=stddev)) if wl is not None: # 给weight加一个L2的loss,相当于做了一个L2的正则化处理 # 在机器学习中,不管是分类还是回归任务,都可能因为特征过多而导致过拟合,一般可以通过减少特征或者惩罚不重要特征的权重来缓解这个问题 # 但是通常我们并不知道该惩罚哪些特征的权重,而正则化就是帮助我们惩罚特征权重的,即特征的权重也会成为模型的损失函数的一部分 # 我们使用w1来控制L2 loss的大小 weight_loss = tf.multiply(tf.nn.l2_loss(var), wl, name='weight_loss') # 我们使用tf.add_to_collection把weight loss统一存到一个collection,这个collection名为"losses",它会在后面计算神经网络 # 总体loss时被用上 tf.add_to_collection("losses", weight_loss) return var # 下载cifar10类下载数据集,并解压,展开到其默认位置 cifar10.maybe_download_and_extract() # 使用cifar10_input类中的distorted_inputs函数产生训练需要使用的数据,包括特征及其对应的label,这里是封装好的tensor, # 每次执行都会生成一个batch_size的数量的样本。需要注意的是这里对数据进行了Data Augmentation数据增强 # 具体实现细节查看函数,其中数据增强操作包括随机水平翻转tf.image.random_flip_left_right() # 随机剪切一块24*24大小的图片tf.random_crop,随机设置亮度和对比度,tf.image.random_brightness、tf.image.random_contrast # 以及对数据进行标准化,白化 tf.image.per_image_standardization() 减去均值、除以方差,保证数据零均值,方差为1 images_train, labels_train = cifar10_input.distorted_inputs( data_dir=data_dir, batch_size=batch_size ) # 生成测试数据,不过这里不需要进行太多处理,不需要对图片进行翻转或修改亮度、对比度,不过需要裁剪图片正中间的24*24大小的区块, # 并进行数据标准化操作 images_test, labels_test = cifar10_input.inputs(eval_data=True, data_dir=data_dir, batch_size=batch_size) # 因为batch_size在之后定义网络结构时被用到了,所以数据尺寸中的第一个值即样本条数需要被预先设定,而不能像以前那样设置为None # 而数据尺寸中的图片尺寸为24*24即是剪裁后的大小,颜色通道数则设为3 image_holder = tf.placeholder(tf.float32, [batch_size, 24, 24, 3]) label_holder = tf.placeholder(tf.int32, [batch_size]) # 初始设置第一个卷积层,64个卷积核,卷积核大小是5*5,3通道 weight1 = variable_with_weight_losses(shape=[5, 5, 3, 64], stddev=5e-2, wl=0.0) kernel1 = tf.nn.conv2d(image_holder, filter=weight1, strides=[1, 1, 1, 1], padding='SAME') bias1 = tf.Variable(tf.constant(0.0, shape=[64])) conv1 = tf.nn.relu(tf.nn.bias_add(kernel1, bias1)) # 使用尺寸3*3步长2*2的最大池化层处理数据,这里最大池化的尺寸和步长不一样,可以增加数据的丰富性 pool1 = tf.nn.max_pool(conv1, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1], padding='SAME') # 使用LRN对结果进行处理 # LRN最早见于Alex那篇用CNN参加ImageNet比赛的论文,Alex在论文中解释LRN层模仿了生物神经系统的"侧抑制"机制, # 对局部神经元的活动创建竞争环境,使得其中响应比较大的值变得相对更大,并抑制其他反馈较小的神经元,增强了模型的泛化能力 # Alex在ImageNet数据集上的实验表明,使用LRN后CNN在Top1的错误率可以降低1.4%,因此其在经典AlexNet中使用了LRN层 # LRN对ReLU这种没有上限边界的激活函数会比较有用,因为它会从附近的多个卷积核的响应中挑选比较大的反馈 # 但不适合Sigmoid这种有固定边界并且能抑制过大值得激活函数 norm1 = tf.nn.lrn(pool1, 4, bias=1.0, alpha=0.001 / 9.0, beta=0.75) # 创建第二个卷积层 # 上面64个卷积核,即输出64个通道,所以本层卷积核尺寸的第三个维度即输入的通道数也需要调整为64 weight2 = variable_with_weight_losses(shape=[5, 5, 64, 64], stddev=5e-2, wl=0.0) kernel2 = tf.nn.conv2d(norm1, weight2, [1, 1, 1, 1], padding='SAME') # 还有这里的bias值全部初始化为0.1,而不是0.最后,调换了最大池化层和LRN层的顺序,先进行LRN层处理,再使用最大池化层 bias2 = tf.Variable(tf.constant(0.1, shape=[64])) conv2 = tf.nn.relu(tf.nn.bias_add(kernel2, bias2)) norm2 = tf.nn.lrn(conv2, 4, bias=1.0, alpha=0.001 / 9.0, beta=0.75) pool2 = tf.nn.max_pool(norm2, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1], padding='SAME') # 两个卷积层之后,是全连接层 # 先把第二个卷积层之后的输出结果flatten,使用tf.reshape函数将每个样本都变成一维向量,使用get_shape函数获取数据扁平化之后的长度 reshape = tf.reshape(pool2, [batch_size, -1]) dim = reshape.get_shape()[1].value # 接着初始化权值,隐含节点384个,正太分布的标准差设为0.04,bias的值也初始化为0.1 # 注意这里我们希望这个全连接层不要过拟合,因此设了一个非零的weight loss值0.04,让这一层具有L2正则所约束。 weight3 = variable_with_weight_losses(shape=[dim, 384], stddev=0.04, wl=0.004) bias3 = tf.Variable(tf.constant(0.1, shape=[384])) # 最后我们依然使用ReLU激活函数进行非线性化 local3 = tf.nn.relu(tf.matmul(reshape, weight3) + bias3) # 接下来还是全连接层,只是隐含节点只有一半,其他一样 weight4 = variable_with_weight_losses(shape=[384, 192], stddev=0.04, wl=0.004) bias4 = tf.Variable(tf.constant(0.1, shape=[192])) local4 = tf.nn.relu(tf.matmul(local3, weight4) + bias4) # 最后一层,依然先创建一层weight,其正太分布标准差设为一个隐含层节点数的倒数,并且不用L2正则 # 这里没有用之前的softmax输出最后结果,这里把softmax操作放在了计算loss部分,其实我们不需要对inference的输出进行softmax # 处理就可以获得最终分类结果(直接比较inference输出的各类的数值大小即可),计算softmax主要是为了计算loss,因此softmax操作整合到后面合理 weight5 = variable_with_weight_losses(shape=[192, 10], stddev=1/192.0, wl=0.0) bias5 = tf.Variable(tf.constant(0.0, shape=[10])) logits = tf.add(tf.matmul(local4, weight5), bias5) # 到这里就完成了整个网络inference的部分,梳理整个网络结构,设计性能良好的CNN是有一定规律可循的,但是想要针对某个问题设计最合适的 # 网络结构,是需要大量实际摸索的 # 完成模型inference的构建,接下来是计算CNN的loss,这里依然是用cross_entropy,这里我们把softmax的计算和cross_entropy的计算 # 合在了一起,即 tf.nn.sparse_softmax_cross_entropy_with_logits() # 这里使用 tf.reduce_mean() 对 cross entropy计算均值,再使用 tf.add_to_collection()把cross entropy的loss添加到整体 # losses的collection中,最后,使用tf.add_n将整体losses的collection集合中的全部loss求和,得到最终的loss,其中包括 # cross entropy loss, 还有后两个全连接层中weight的L2 loss def loss(logits, labels): labels = tf.cast(labels, tf.int64) cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits( logits=logits, labels=labels, name='cross_entropy_per_example' ) cross_entropy_mean = tf.reduce_mean(cross_entropy, name='cross_entropy') tf.add_to_collection('losses', cross_entropy_mean) return tf.add_n(tf.get_collection('losses'), name='total_loss') loss = loss(logits=logits, labels=label_holder) # 优化器依然选择Adam Optimizer, 学习速率0.001 train_op = tf.train.AdamOptimizer(1e-3).minimize(loss) # 使用 tf.nn.in_top_k()函数求输出结果中 top k的准确率,默认使用top 1,也就是输出分数最高的那一类的准确率 top_k_op = tf.nn.in_top_k(logits, label_holder, 1) sess = tf.InteractiveSession() tf.global_variables_initializer().run() # 前面对图像进行数据增强的操作需要耗费大量CPU时间,因此distorted_inputs使用了16个独立的线程来加速任务,函数内部会产生线程池, # 在需要使用时会通过TensorFlow queue进行调度 # 启动图片数据增强的线程队列,这里一共使用了16个线程来进行加速,如果不启动线程,那么后续inference以及训练的操作都是无法开始的 tf.train.start_queue_runners() # 进行训练 for step in range(max_steps): start_time = time.time() image_batch, label_batch = sess.run([images_train, labels_train]) _, loss_value = sess.run([train_op, loss], feed_dict={image_holder: image_batch, label_holder: label_batch}) duration = time.time() - start_time if step % 10 == 0: examples_per_sec = batch_size / duration sec_per_batch = float(duration) format_str = 'step %d, loss = %.2f (%.1f examples/sec; %.3f sec/batch)' print(format_str % (step, loss_value, examples_per_sec, sec_per_batch)) # 评测模型在测试集上的准确率 # 我们依然像训练时那样使用固定的batch_size,然后一个batch一个batch输入测试数据 num_examples = 10000 # 先计算一共要多少个batch才能将全部样本评测完 num_iter = int(math.ceil(num_examples / batch_size)) true_count = 0 total_sample_count = num_iter * batch_size step = 0 while step < num_iter: image_batch, label_batch = sess.run([images_test, labels_test]) predictions = sess.run([top_k_op], feed_dict={image_holder: image_batch, label_holder: label_batch}) true_count += np.sum(predictions) step += 1 precision = true_count / total_sample_count print('precision @ 1 = %.3f' % precision) # 最终,在cifar-10数据集上,通过一个短时间小迭代的训练,可以达到大致73%的准确率,持续增加max_steps,可以期望准确率逐渐增加 # 如果max_steps比较大,则推荐使用学习速率衰减decay的SGD进行训练,这样训练过程中能达到的准确率峰值会比较高,大致有86% # 其中L2正则以及LRN层的使用都对模型准确率有提升作用,它们都可以提升模型的泛化能力 # 数据增强Data Augmentation在我们的训练中作用很大,它可以给单幅图增加多个副本,提高图片的利用率,防止对某一张图片结构的学习过拟合 # 这刚好是利用了图片数据本身的性质,图片的冗余信息量比较大,因此可以制造不同的噪声并让图片依然可以被识别出来。如果神经网络可以克服这些 # 噪声并准确识别,那么他的泛化能力必然很好。数据增强大大增加了样本量,而数据量的大小恰恰是深度学习最看重的,深度学习可以在图像识别上领先 # 其他算法的一大因素就是它对海量数据的利用效率非常高。其他算法,可能在数据量大到一定程度时,准确率就不再上升了,而深度学习只要提供足够 # 多的样本,准确率基本持续提升,所以说它是最适合大数据的算法 梯度弥散/消失(Vanishing Gradients):在梯度下降中,随着算法反向反馈到前面几层,梯度会越来越小,最终没有变化,这时或许还没有收敛到比较好的解即权重值几乎不改变 解决梯度消失的三个思想: 改变激活函数: 不饱和激活函数ReLU解决正数的梯度但负数的梯度为0,ReLU激活函数相关的变形函数:leaky ReLU,max(a*z,z),a=0.01,z=0时不可导,需要手动实现函数 RReLU,Random,a是一个在给定范围内随机取值的数在训练时,固定的平 均值在测试时,过拟合可以试试 PReLU,Parametric,a是一个在训练过程中需要学习的超参数,它会被修改 在反向传播中,适合大数据集 ELU,exponential,计算梯度的速度会慢一些,但是整体因为没有死的神经元 ,整体收敛快,超参数0.01,TensorFlow框架中有封装 理论上激活函数的排序:ELU > leaky ReLU > ReLU > tanh > logistic 控制初始化权重值W: Xavier Initialization:每层输出的方差等于它的输入的方差,并且我们同时需要 梯度有相同的方差,当反向传播进入这层时和离开这层时上面理论不能同时保证,除非层有相同的输入连接和输出连接,但是有一个不错的妥协在实际验证中,连接权重被随机初始化,n_inputs和n_outputs是输入和输出的连接,也叫fan_in和fan_out, 这种初始化的策略叫Xaiver initialization 初始化策略Xaiver initialization的变形He Initialization:fully_connected()函数默认使用Xavier初始化对应uniform distribution,可以修改为He initialization使用variance_scaling_initializer()函数 数据归一化: He initialization和ELU可以减少梯度弥散问题在开始训练时,但是不保证在训练的后面不会发生,Batch Normalization可以更好解决问题,它应用于每层激活函数之前对每一批次数据做均值和方差归一化,类似对图像进行放大缩小平移,LeNet和AlexNet架构中使用的LRN激活函数的N是某种归一化方式 反向传播(Backpropagation):梯度下降使用reverse-mode autodiff 前向传播:求预测值make predictions,然后计算输出误差,然后计算出每个神经元节点对误差的贡献,求贡献是反向传播的方式是根据前向传播的误差来求梯度,然后根据贡献调整原来的权重 反向自动求导(Reverse-mode Autodiff):TensorFlow实现的方案,首先,它执行图 的前向阶段,从输入到输出,去计算节点值,然后是反向阶段,从输出到输入去计算所有的偏导 from datetime import datetime import math import time import tensorflow as tf # ILSVRC(ImageNet Large Scale Visual Recognition Challenge) # ImageNet项目于2007年由斯坦福大学华人教授李飞飞创办,目标是收集大量带有标注信息的图片数据供计算机视觉模型训练 # ImageNet拥有1500万张标注过的高清图片,总共拥有22000类,其中约有100万张标注了图片中主要物体的定位边框 # ImageNet项目最早的灵感来自于人类通过视觉学习世界的方式,如果假定儿童的眼睛是生物照相机,它们平均每200ms就拍照一次 # 眼球转动一次的平均时间200ms,那么3岁大的孩子就已经看过了上亿张真实时间的照片,使用亚马逊的土耳其机器人平台实现标注过程 # 来自世界上167个国家的5万名工作者帮忙一起筛选、标注 # 每年ILSVRC比赛数据集中大概有120万张图片,以及1000类的标注,是ImageNet全部数据的一个子集。比赛采用top-5和top-1分类错误率 # 作为模型性能的评测指标 # AlexNet比赛分类项目的2012年冠军,top5错误率16.4%,8层神经网络 # 神经网络模型AlexNet可以算是LeNet的一种更深更宽的版本!AlexNet中包含了几个比较新的技术点,首次在CNN中成功应用了ReLU、Dropout、 # LRN等Trick,AlexNet包含了6亿3000万个连接,6000多万个参数!和65万个神经元,拥有5个卷积层,3个全连接层,其中3个卷积层后面 # 连接了最大池化层,输出层是1000类的softmax层做分类,LRN应用在了第一卷积层和第二卷积层后面,ReLU激活函数应用在8层每一层后面 # 1,运用ReLU,解决Sigmoid在网络层次较深时的梯度弥散 # 2,训练Dropout,随机忽略一些神经元,避免过拟合 # 3,使用重叠的最大池化,此前CNN普遍平均池化,最大池化避免平均池化的模糊化效果 # 4,提出了LRN层,局部神经元活动创建竞争机制,响应比较大的值变得更大,抑制其他反馈小的神经元,增强泛化能力 # 5,使用CUDA加速深度卷积网络的训练 # 6,数据增强,随机地从256*256的原始图像中截取224*224大小的区域,以及水平翻转的镜像,相当于增加了【(256-224)^2】*2=2048 # 倍的数据量。没有数据增强,紧靠原始的数据量,参数众多的CNN会陷入过拟合中 batch_size = 32 num_batchs = 100 # 定义一个现实网络每一层结构的函数print_actications,展示每一个卷积层或池化层输入tensor的尺寸 # 这个函数接受一个tensor作为输入,并显示其名称 t.op.name 和tensor尺寸 t.get_shape.as_list() def print_activations(t): print(t.op.name, " ", t.get_shape().as_list()) def inference(images): parameters = [] with tf.name_scope('conv1') as scope: kernel = tf.Variable(tf.truncated_normal([11, 11, 3, 64], dtype=tf.float32, stddev=1e-1), name='weights') conv = tf.nn.conv2d(images, kernel, [1, 4, 4, 1], padding='SAME') biases = tf.Variable(tf.constant(0.0, shape=[64], dtype=tf.float32), trainable=True, name='biases') bias = tf.nn.bias_add(conv, biases) conv1 = tf.nn.relu(bias, name=scope) print_activations(conv1) parameters += [kernel, biases] # 这里LRN参数基本都是AlexNet论文中的推荐值,不过目前除了AlexNet,其他经典的卷积神经网络基本都放弃了LRN # 主要是效果不明显,使用也会使得前馈、反馈的速度整体下降1/3,可以自主选择是否使用LRN lrn1 = tf.nn.lrn(conv1, depth_radius=4, bias=1.0, alpha=0.001/9, beta=0.75, name='lrn1') pool1 = tf.nn.max_pool(lrn1, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1], padding='VALID', name='pool1') print_activations(pool1) with tf.name_scope('conv2') as scope: kernel = tf.Variable(tf.truncated_normal([5, 5, 64, 192], dtype=tf.float32, stddev=1e-1, name='weights')) conv = tf.nn.conv2d(pool1, kernel, [1, 1, 1, 1], padding='SAME') biases = tf.Variable(tf.constant(0.0, shape=[192], dtype=tf.float32), trainable=True, name='biases') bias = tf.nn.bias_add(conv, biases) conv2 = tf.nn.relu(bias, name=scope) parameters += [kernel, biases] print_activations(conv2) lrn2 = tf.nn.lrn(conv2, 4, bias=1.0, alpha=0.001/9, beta=0.75, name='lrn2') pool2 = tf.nn.max_pool(lrn2, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1], padding='VALID', name='pool2') print_activations(pool2) with tf.name_scope('conv3') as scope: kernel = tf.Variable(tf.truncated_normal([3, 3, 192, 384], dtype=tf.float32, stddev=1e-1, name='weights')) conv = tf.nn.conv2d(pool2, kernel, [1, 1, 1, 1], padding='SAME') biases = tf.Variable(tf.constant(0.0, shape=[384], dtype=tf.float32), trainable=True, name='biases') bias = tf.nn.bias_add(conv, biases) conv3 = tf.nn.relu(bias, name=scope) parameters += [kernel, biases] print_activations(conv3) with tf.name_scope('conv4') as scope: kernel = tf.Variable(tf.truncated_normal([3, 3, 384, 256], dtype=tf.float32, stddev=1e-1, name='weights')) conv = tf.nn.conv2d(conv3, kernel, [1, 1, 1, 1], padding='SAME') biases = tf.Variable(tf.constant(0.0, shape=[256], dtype=tf.float32), trainable=True, name='biases') bias = tf.nn.bias_add(conv, biases) conv4 = tf.nn.relu(bias, name=scope) parameters += [kernel, biases] print_activations(conv4) with tf.name_scope('conv5') as scope: kernel = tf.Variable(tf.truncated_normal([3, 3, 256, 256], dtype=tf.float32, stddev=1e-1, name='weights')) conv = tf.nn.conv2d(conv4, kernel, [1, 1, 1, 1], padding='SAME') biases = tf.Variable(tf.constant(0.0, shape=[256], dtype=tf.float32), trainable=True, name='biases') bias = tf.nn.bias_add(conv, biases) conv5 = tf.nn.relu(bias, name=scope) parameters += [kernel, biases] print_activations(conv5) pool5 = tf.nn.max_pool(conv5, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1], padding='VALID', name='pool5') print_activations(pool5) return pool5, parameters # 最后我们返回这个池化层的输出pool5,这样inference函数就完成了,它可以创建AlexNet的卷积部分,在正式使用AlexNet来训练或预测时 # 还需要添加3个全连接层,隐含节点数分别为4096,4096,1000,由于最后3个全连接层的计算量很小,就没有房子计算速度评测中 # 大家在使用AlexNet时需要自行加上这3个全连接层 # 评估AlexNet每轮计算时间的函数 def time_tensorflow_run(session, target, info_string): num_steps_burn_in = 10 # 预热轮数 total_duration = 0.0 total_duration_squared = 0.0 for i in range(num_batchs + num_steps_burn_in): start_time = time.time() _ = session.run(target) duration = time.time() - start_time if i >= num_steps_burn_in: if not i % 10: print('%s: step %d, duration = %.3f' % (datetime.now(), i - num_steps_burn_in, duration)) total_duration += duration total_duration_squared += duration * duration mn = total_duration / num_batchs vr = total_duration_squared / num_batchs - mn * mn sd = math.sqrt(vr) print('%s: %s across %d steps, %.3f +/- %.3f sec / batch' % (datetime.now(), info_string, num_batchs, mn, sd)) def run_benchmark(): with tf.Graph().as_default(): image_size = 224 images = tf.Variable(tf.random_normal([batch_size, image_size, image_size, 3], dtype=tf.float32, stddev=1e-1)) pool5, parameters = inference(images) init = tf.global_variables_initializer() sess = tf.Session() sess.run(init) time_tensorflow_run(sess, pool5, "Forward") # 模拟训练过程 objective = tf.nn.l2_loss(pool5) grad = tf.gradients(objective, parameters) time_tensorflow_run(sess, grad, "Forward-backward") run_benchmark() Keras深度学习库可以简单快速的原型设计(通过用户友好性,模块化和可扩展性)比TensorFlow简洁,官方地址:https://keras.io/ Keras为图片数据输入提供了一个很好的接口,即Keras.preprocessing.image.ImageDataGenerator类,这个类生成一个数据生成器Generator对象,依照循环批量产生对应于图像信息的多维矩阵,根据后台运行环境的不同,比如是TensorFlow还是Theano,多维矩阵的不同维度对应的信息分别是图像二维的像素点,第三维对应于色彩通道,因此如果是灰度图像,那么色彩通道只有一个维度;如果是RGB色彩,那么色彩通道有三个维度 序列模型:属于通用模型的一种,模型各层之间,是依次顺序的线性关系,在第k层和第k+1层之间可以加上各种元素来构造神经网络,这些元素可以通过一个列表来制定,然后作为参数传递给序列模型来生成相应的模型 from keras.models import Sequential引入序列模型模块 from keras.layers import Dense引入全连接层模块 from keras.layers import Activation引入激活函数模块 # Dense相当于构建一个全连接层,32指的是全连接层上面神经元的个数 layers = [Dense(32, input_shape=(784,)), Activation('relu'), Dense(10), Activation('softmax')]定义神经网络拓扑结构列表 model = Sequential(layers)以列表形式构建神经网络拓扑结构的序列模型 # model = Sequential()定义序列模型 # model.add(Dense(32, input_shape=(784,)))以加入形式构建神经网络拓扑结构的序列模型 # model.add(Activation('relu')) # model.add(Dense(10)) # model.add(Activation('softmax')) # model.summary() model.summary()获取神经网络拓扑结构的序列模型的摘要信息 通用模型:可以用来设计非常复杂、任意拓扑结构的神经网络入如有向无环图网络,类似于序列模型,通用模型通过函数化的应用接口来定义模型,使用函数化的应用接口有好多好处如决定函数执行结果的唯一要素是其返回值,而决定返回值的唯一要素则是其参数,这减轻了代码测试的工作量,通用模型中,定义的时候从输入的多维矩阵开始,然后定义各层及其要素,最后定义输出层,将输入层和输出层作为参数纳入通用模型中就可以定义一个模型对象 from keras.layers import Input引入模型输入模块 from keras.layers import Dense引入全连接模块 from keras.models import Model引入模型模块 input = Input(shape=(784,)) 定义输入层 x = Dense(64, activation='relu')(input)定义上一层为input当前层神经元节点为64激活函数为activation的全连接隐藏层 x = Dense(64, activation='relu')(x) y = Dense(10, activation='softmax')(x)定义输出层 model = Model(inputs=input, outputs=y)定义输入为inputs输出为outputs的模型 # 当模型对象定义完成之后,就可以进行编译了,并对数据进行拟合,拟合的时候也有两个参数 # 分别对应于输入和输出 model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy'])定义算法优化器为optimizer损失函数为loss评估指标为metrics的模型编译 model.fit(data, labels)训练模型 使用Keras库实现MNIST数据集的分类: import numpy as np from keras.datasets import mnist from keras.models import Sequential from keras.layers import Dense from keras.layers import Dropout from keras.layers import Flatten from keras.layers.convolutional import Conv2D from keras.layers.convolutional import MaxPooling2D (X_train, y_train), (X_test, y_test) = mnist.load_data("../test_data_home")加载数据集 print(X_train[0].shape)获取数据集形状 print(y_train[0]) X_train = X_train.reshape(X_train.shape[0], 28, 28, 1).astype('float32')将训练集中的手写黑白字体变成标准的四维张量形式,即(样本数量,长,宽,1),像素值转换为浮点格式 X_test = X_test.reshape(X_test.shape[0], 28, 28, 1).astype('float32') # 由于每个像素值都介于0到255,所以这里统一除以255,把像素值控制在0-1范围即数据归一化 X_train /= 255 X_test /= 255 def tran_y(y):将目标数字0-9转换为One Hot编码 y_ohe = np.zeros(10) y_ohe[y] = 1 return y_ohe # 把标签用One Hot编码重新表示一下 y_train_ohe = np.array([tran_y(y_train[i]) for i in range(len(y_train))]) y_test_ohe = np.array([tran_y(y_test[i]) for i in range(len(y_test))]) # 搭建卷积神经网络 model = Sequential() # 添加一层卷积层,构造64个过滤器,每个过滤器覆盖范围是3*3*1 # 过滤器步长为1,图像四周补一圈0,并用relu进行非线性变化 model.add(Conv2D(filters=64, kernel_size=(3, 3), strides=(1, 1), padding='same', input_shape=(28, 28, 1), activation='relu')) # 添加一层最大池化层 model.add(MaxPooling2D(pool_size=(2, 2))) # 设立Dropout层,Dropout的概率为0.5 model.add(Dropout(0.5)) # 重复构造,搭建深度网络 model.add(Conv2D(128, kernel_size=(3, 3), strides=(1, 1), padding='same', activation='relu')) model.add(MaxPooling2D(pool_size=(2, 2))) model.add(Dropout(0.5)) model.add(Conv2D(256, kernel_size=(3, 3), strides=(1, 1), padding='same', activation='relu')) model.add(MaxPooling2D(pool_size=(2, 2))) model.add(Dropout(0.5)) # 把当前层节点展平 model.add(Flatten())将特征图转换成一维像素作为下一层输入 # 构造全连接层神经网络层 model.add(Dense(128, activation='relu')) model.add(Dense(64, activation='relu')) model.add(Dense(32, activation='relu')) model.add(Dense(10, activation='softmax')) # 定义损失函数,一般来说分类问题的损失函数都选择采用交叉熵 model.compile(loss='categorical_crossentropy', optimizer='adagrad', metrics=['accuracy']) # 放入批量样本,进行训练 model.fit(X_train, y_train_ohe, validation_data=(X_test, y_test_ohe) , epochs=20, batch_size=128)训练数据集并使用validation_data验证集所有数据集训练20轮次每次梯度下降使用batch_size批量数据 scores = model.evaluate(X_test, y_test_ohe, verbose=0)使用测试集评价模型的准确率,进度表示方式verbose不显示数据0显示进度条1 模型迁移思想:复用预先训练完成的模型的神经网络层,减少权重值W的计算量 # 使用迁移学习的思想,以VGG16作为模板搭建模型,训练识别手写字体 from keras.applications.vgg16 import VGG16引入VGG16模块 # 其次加载其他模块 from keras.layers import Input from keras.layers import Flatten from keras.layers import Dense from keras.layers import Dropout from keras.models import Model from keras.optimizers import SGD # 加载字体库作为训练样本 from keras.datasets import mnist # 加载OpenCV(在命令行中窗口中输入pip install opencv-python),这里为了后期对图像的处理, # 大家使用pip install C:\Users\28542\Downloads\opencv_python-3.4.1+contrib-cp35-cp35m-win_amd64.whl # 比如尺寸变化和Channel变化。这些变化是为了使图像满足VGG16所需要的输入格式 import cv2 import h5py as h5py import numpy as np # 建立一个模型,其类型是Keras的Model类对象,我们构建的模型会将VGG16顶层去掉,只保留其余的网络 # 结构。这里用include_top = False表明我们迁移除顶层以外的其余网络结构到自己的模型中 # VGG模型对于输入图像数据要求高宽至少为48个像素点,由于硬件配置限制,我们选用48个像素点而不是原来 # VGG16所采用的224个像素点。即使这样仍然需要24GB以上的内存,或者使用数据生成器 model_vgg = VGG16(include_top=False, weights='imagenet', input_shape=(48, 48, 3))获取VGG16模型的部分神经网络层 for layer in model_vgg.layers: layer.trainable = False设置神经网络层不进行训练 model = Flatten(name='flatten')(model_vgg.output)在VGG16模型基础上添加神经网络层 model = Dense(4096, activation='relu', name='fc1')(model) model = Dense(4096, activation='relu', name='fc2')(model) model = Dropout(0.5)(model) model = Dense(10, activation='softmax')(model) model_vgg_mnist = Model(inputs=model_vgg.input, outputs=model, name='vgg16') # 打印模型结构,包括所需要的参数 model_vgg_mnist.summary() model_vgg = VGG16(include_top=False, weights='imagenet', input_shape=(224, 224, 3)) for layer in model_vgg.layers: layer.trainable = False model = Flatten()(model_vgg.output) model = Dense(4096, activation='relu', name='fc1')(model) model = Dense(4096, activation='relu', name='fc2')(model) model = Dropout(0.5)(model) model = Dense(10, activation='softmax', name='prediction')(model) model_vgg_mnist_pretrain = Model(model_vgg.input, model, name='vgg16_pretrain') model_vgg_mnist_pretrain.summary() # 新的模型不需要训练原有卷积结构里面的1471万个参数,但是注意参数还是来自于最后输出层前的两个 # 全连接层,一共有1.2亿个参数需要训练 sgd = SGD(lr=0.05, decay=1e-5)获取随机小批量梯度下降算法 model_vgg_mnist.compile(loss='categorical_crossentropy', optimizer=sgd, metrics=['accuracy']) # 因为VGG16对网络输入层的要求,我们用OpenCV把图像从32*32变成224*224,把黑白图像转成RGB图像 # 并把训练数据转化成张量形式,供keras输入 (X_train, y_train), (X_test, y_test) = mnist.load_data("../test_data_home") X_train, y_train = X_train[:10000], y_train[:10000] X_test, y_test = X_test[:1000], y_test[:1000] X_train = [cv2.cvtColor(cv2.resize(i, (48, 48)), cv2.COLOR_GRAY2RGB) for i in X_train]将图像数据进行转换缩放 X_train = np.concatenate([arr[np.newaxis] for arr in X_train]).astype('float32') X_test = [cv2.cvtColor(cv2.resize(i, (48, 48)), cv2.COLOR_GRAY2RGB) for i in X_test] X_test = np.concatenate([arr[np.newaxis] for arr in X_test]).astype('float32') print(X_train.shape) print(X_test.shape) X_train = X_train / 255 X_test = X_test / 255 def tran_y(y): y_ohe = np.zeros(10) y_ohe[y] = 1 return y_ohe y_train_ohe = np.array([tran_y(y_train[i]) for i in range(len(y_train))]) y_test_ohe = np.array([tran_y(y_test[i]) for i in range(len(y_test))]) model_vgg_mnist.fit(X_train, y_train_ohe, validation_data=(X_test, y_test_ohe), epochs=100, batch_size=50) 深度学习优化算法比较:SGD、Adagrad、Adadelta、Adam、Adamax、Nadam SGD:常用SGD一般是mini-batch gradient descent,数据量大时最好优化算法 Momentum:模拟物理里动量的概念,积累之前的动量来替代真正的梯度 Adagrad:对学习率进行一个约束 Adadelta:对Adagrad的扩展,最初方案依然是对学习率进行自适应约束,但是进行了计算上的简化。 Adagrad会累加之前所有的梯度平方,而Adadelta只累加固定大小的项,并且也不直接存储这些项,仅仅是近似计算对应的平均值。 RMSprop:可以算作Adadelta的一个特例 Adam(Adaptive Moment Estimation):带有动量项的RMSprop,它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率