莫烦PYTHON | Tensorflow教程——建造我们第一个神经网络(第三章)
#3.1 例子3 添加层def add_layer()
为神经网络添加一个神经层
import tensorflow as tf
#添加一个神经层
def add_layer(inputs, in_size, out_size, activation_function = None):
Weights = tf.Variable(tf.random_normal([in_size,out_size])) #in_size代表行/输入层
biases = tf.Variable(tf.zeros([1,out_size]) + 0.1)
Wx_plus_b = tf.matmul(inputs,Weights) + biases #Wx_plus_b代表W*x+b
if activation_function is None: #如果没有激励函数,即为线性关系,那么直接输出,不需要激励函数(非线性函数)
outputs = Wx_plus_b
else:
outputs = activation_function(Wx_plus_b) #把这个值传进去
return outputs
#3.2 例子3 建造神经网络
构建一个简单的神经网络来预测y=x^2
import tensorflow as tf
import numpy as np
#添加一个神经层,定义添加神经层的函数
def add_layer(inputs, in_size, out_size, activation_function = None):
Weights = tf.Variable(tf.random_normal([in_size,out_size])) #in_size代表行/输入层
biases = tf.Variable(tf.zeros([1,out_size]) + 0.1)
Wx_plus_b = tf.matmul(inputs,Weights) + biases #Wx_plus_b代表W*x+b
if activation_function is None: #如果没有激励函数,即为线性关系,那么直接输出,不需要激励函数(非线性函数)
outputs = Wx_plus_b
else:
outputs = activation_function(Wx_plus_b) #把这个值传进去
return outputs
x_data = np.linspace(-1, 1, 300, dtype = np.float32)[:, np.newaxis] #输入,np.float32改变数组的长度显示,linspace创建一个从-1到1的等差数列,默认为50个数,这里规定了要生成300个数,并且使用[:, np.newaxis]将数组转换为列向量,[np.newaxis,:]可转换为行向量
noise = np.random.normal(0, 0.05, x_data.shape).astype(np.float32) #生成一个均值/中心为0,标准差/宽度为0.05的正太分布作为噪点/干扰点,它的格式为x_data,使得我们想要预测的函数更加接近实际情况;astype转换数据类型格式为float32
y_data = np.square(x_data) - 0.5 + noise #x的平方减去一个任意值再加上噪点
xs = tf.placeholder(tf.float32, [None, 1]) #占位符,保存数据的利器,float32数据类型,[None,1]表示列为1,行不定的列向量;xs表示x_Session,因为placeholder是与Session一起用的,它在使用的时候和前面的variable不同的是在session运行阶段,需要给placeholder提供数据,利用feed_dict的字典结构给placeholdr变量“喂数据”;placeholder的语法:tf.placeholder(dtype, shape=[None,None] [, name=None])
ys = tf.placeholder(tf.float32, [None, 1])
l1 = add_layer(xs, 1, 10, activation_function = tf.nn.relu) #创建一个隐藏层l1,输入为xs,输入的层数/神经元的个数1=输入层,输出的层数10=隐藏层中神经元的个数
prediction = add_layer(l1, 10, 1, activation_function = None) #预测值;定义输出层,输入为l1=前一层隐藏层的输出,输入的层数为10=隐藏层神经元的个数,输出的层数为1=输出一般只有1层
loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys-prediction),reduction_indices = [1])) #计算预测值prediction与真实值ys的误差:所有的平方差相加再求平均;reduction_indices = [1]表示相加的方法,[1]表示行求和,[0]表示列求和,具体解释见下文
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss) #机器要学习的内容,使用优化器提升准确率,学习率为0.1<1,表示以0.1的效率来最小化误差loss
init = tf.global_variables_initializer() #使用变量,就要对其初始化
sess = tf.Session() #定义Session,并使用Session来初始化步骤
sess.run(init)
for i in range(1000): #训练1000次
sess.run(train_step, feed_dict={xs:x_data, ys:y_data}) #给placeholder喂数据,把x_data赋值给xs
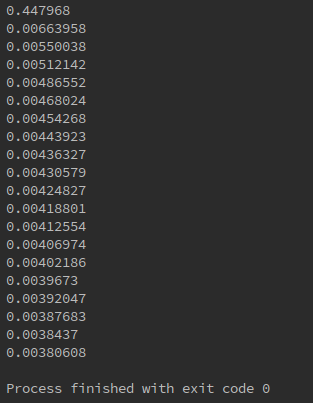
if i % 50 == 0: #每50步输出一次机器学习的误差
print(sess.run(loss, feed_dict={xs:x_data, ys:y_data}))
##关于reduce_sum()函数:
在tensorflow中使用加法函数,同时需要reduction_indices=[1, 0],[1]表示行求和,[0]表示列求和。
下图中[3, 3]竖起来显示是为了说明reduction_indices这个过程中维度的信息是一直保留的,所以它并不是一个列向量,所以它不是[ [3], [3] ],它本质还是[3, 3],所以说无论是行求和还是列求和最后输出都被转换成行向量。
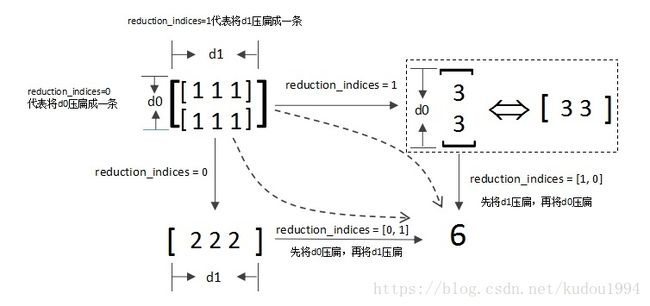
转自知乎用户:凡心 reduction_indices的解释
#3.3 例子3 结果可视化
#import os
#os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
#添加一个神经层,定义添加神经层的函数
def add_layer(inputs, in_size, out_size, activation_function = None):
Weights = tf.Variable(tf.random_normal([in_size,out_size])) #in_size代表行/输入层
biases = tf.Variable(tf.zeros([1,out_size]) + 0.1)
Wx_plus_b = tf.matmul(inputs,Weights) + biases #Wx_plus_b代表W*x+b
if activation_function is None: #如果没有激励函数,即为线性关系,那么直接输出,不需要激励函数(非线性函数)
outputs = Wx_plus_b
else:
outputs = activation_function(Wx_plus_b) #把这个值传进去
return outputs
x_data = np.linspace(-1, 1, 300, dtype = np.float32)[:, np.newaxis] #输入,np.float32改变数组的长度显示,linspace创建一个从-1到1的等差数列,默认为50个数,这里规定了要生成300个数,并且使用[:, np.newaxis]将数组转换为列向量,[np.newaxis,:]可转换为行向量
noise = np.random.normal(0, 0.05, x_data.shape).astype(np.float32) #生成一个均值/中心为0,标准差/宽度为0.05的正太分布作为噪点/干扰点,它的格式为x_data,使得我们想要预测的函数更加接近实际情况;astype转换数据类型格式为float32
y_data = np.square(x_data) - 0.5 + noise #x的平方减去一个任意值再加上噪点
xs = tf.placeholder(tf.float32, [None, 1]) #占位符,保存数据的利器,float32数据类型,[None,1]表示列为1,行不定的列向量;xs表示x_Session,因为placeholder是与Session一起用的,它在使用的时候和前面的variable不同的是在session运行阶段,需要给placeholder提供数据,利用feed_dict的字典结构给placeholdr变量“喂数据”;placeholder的语法:tf.placeholder(dtype, shape=[None,None] [, name=None])
ys = tf.placeholder(tf.float32, [None, 1])
l1 = add_layer(xs, 1, 10, activation_function = tf.nn.relu) #创建一个隐藏层l1,输入为xs,输入的层数/神经元的个数1=输入层,输出的层数10=隐藏层中神经元的个数
prediction = add_layer(l1, 10, 1, activation_function = None) #预测值;定义输出层,输入为l1=前一层隐藏层的输出,输入的层数为10=隐藏层神经元的个数,输出的层数为1=输出一般只有1层
loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys-prediction),reduction_indices = [1])) #计算预测值prediction与真实值ys的误差:所有的平方差相加再求平均;reduction_indices = [1]表示相加的方法,[1]表示行求和,[0]表示列求和,具体解释见下文
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss) #机器要学习的内容,使用优化器提升准确率,学习率为0.1<1,表示以0.1的效率来最小化误差loss
init = tf.global_variables_initializer() #使用变量,就要对其初始化
sess = tf.Session() #定义Session,并使用Session来初始化步骤
sess.run(init)
#绘制真实数据
fig = plt.figure() #生成一个画框/画布
ax = fig.add_subplot(1, 1, 1) #将画框分为1行1列,并将图 画在画框的第1个位置
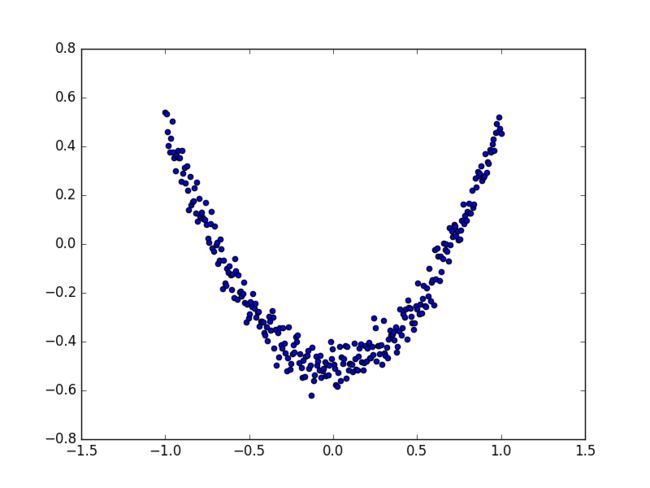
ax.scatter(x_data, y_data) #画散点图
plt.ion() #交互绘制功能,用于连续显示;本次运行时请注释掉这条语句,全局运行不需要注释掉
plt.show() #显示所绘制的图形,但是他只显示当前运行时的图像,不会一直显示多次;在实际运行当中,注释掉上面两条代码,程序才会正常运行,暂时不知道为什么。。。
for i in range(1000): #训练1000次
sess.run(train_step, feed_dict={xs:x_data, ys:y_data}) #给placeholder喂数据,把x_data赋值给xs
if i % 50 == 0: #每50步输出一次机器学习的误差
#print(sess.run(loss, feed_dict={xs:x_data, ys:y_data}))
#可视化结果与改进
try:
ax.lines.remove(lines[0]) #抹去前一条绘制的曲线,在这里我们要先抹去再绘制,防止第一次运行时报错,我们使用try语句
except Exception:
pass
prediction_value = sess.run(prediction, feed_dict={xs:x_data})
#绘制预测数据
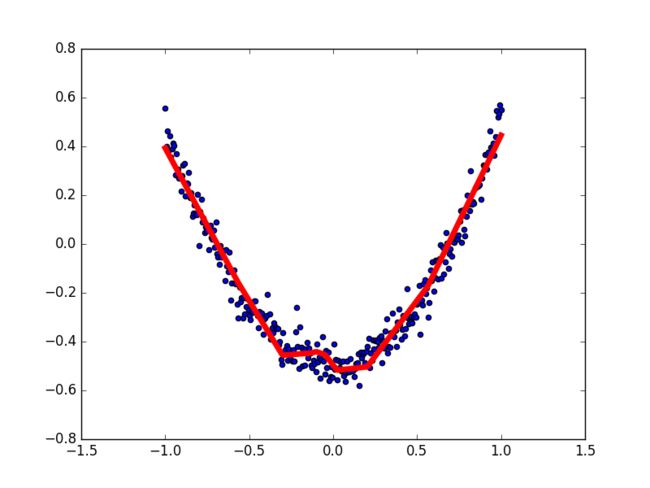
lines = ax.plot(x_data, prediction_value,'r-',lw=5) #x轴数据,y轴数据,红色的线,线的宽度为5
plt.pause(0.1) #绘制曲线的时间间隔为0.1秒
散点图:
训练结果(为什么我的训练结果很差呢?未解决)
##关于add_subplot(1, 1, 1)
这篇文章讲得很不错
#3.4 加速神经网络训练(Speed Up Training)
原文讲的很生动形象:莫烦Python
不过没讲公式,公式看不懂。。。推倒过程不太理解。
如果不适用加速,那么庞大的数据集会让训练变得很慢。
几种加速方法:
###Stochastic Gradient Descent (SGD) 随机梯度下降(初学)
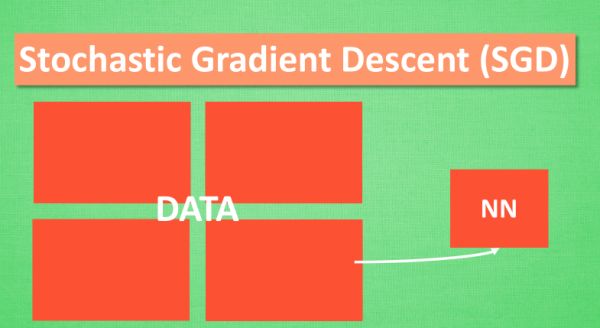
把这些数据拆分成小批小批的, 然后再分批不断放入 NN 中计算,不会丢失太多的准确率。
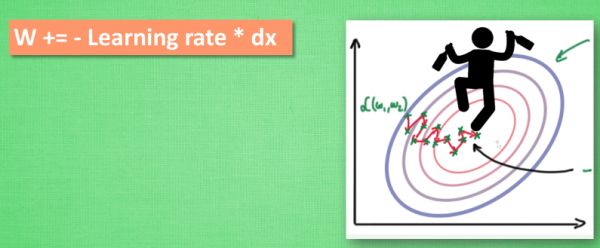
###Momentum(常用)
学习率(learning rate)
校正值 (dx)
更新W
一个形象的例子:大多数其他途径是在更新神经网络参数那一步上动动手脚. 传统的参数 W 的更新是把原始的 W 累加上一个负的学习率(learning rate) 乘以校正值 (dx). 这种方法可能会让学习过程曲折无比, 看起来像喝醉的人回家时, 摇摇晃晃走了很多弯路.
所以我们把这个人从平地上放到了一个斜坡上, 只要他往下坡的方向走一点点, 由于向下的惯性, 他不自觉地就一直往下走, 走的弯路也变少了. 这就是 Momentum 参数更新.
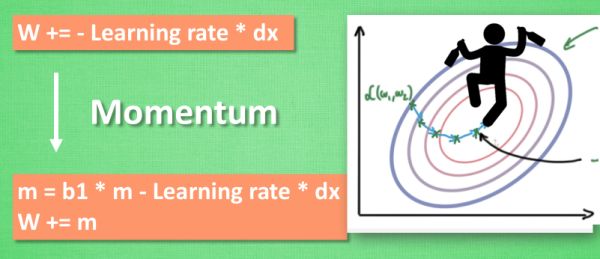
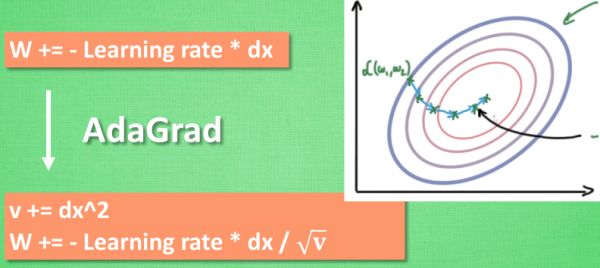
###AdaGrad
在学习率上面动手脚, 使得每一个参数更新都会有自己与众不同的学习率,给他一双不好走路的鞋子, 使得他一摇晃着走路就脚疼, 鞋子成为了走弯路的阻力, 逼着他往前直着走.
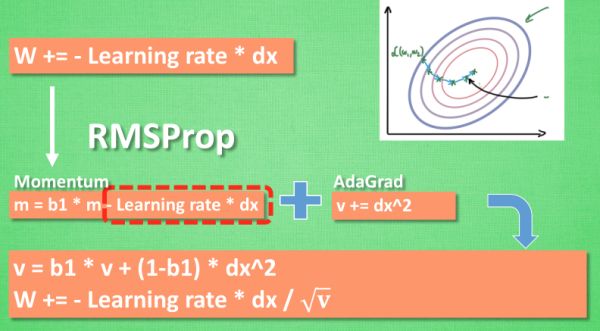
###RMSProp(AlphaGo使用这款优化器来优化)
有了 momentum 的惯性原则 , 加上 adagrad 的对错误方向的阻力, 我们就能合并成这样. 让 RMSProp同时具备他们两种方法的优势. 这种方法还没把 Momentum合并完全, RMSProp 还缺少momentum 中的一部分.
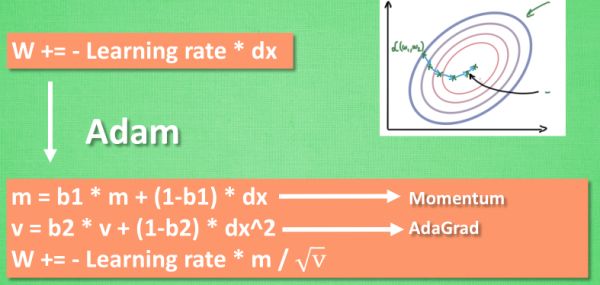
###Adam(常用)
计算m 时有 momentum 下坡的属性, 计算 v 时有 adagrad 阻力的属性, 然后再更新参数时 把 m 和 V 都考虑进去. 实验证明, 大多数时候, 使用 adam 都能又快又好的达到目标, 迅速收敛. 所以说, 在加速神经网络训练的时候, 一个下坡, 一双破鞋子, 功不可没.
#3.5 优化器 optimizer
机器学习中最基础的线性优化
tensorflow的优化器一共有七种
常用见上一节
tf.train 提供了一组有助于训练模型的类和函数。
优化器
Optimizer基类提供了计算损失梯度的方法,并将梯度应用于变量。子类集合实现了经典的优化算法,如GradientDescent和Adagrad。
您永远不会实例化Optimizer类本身,而是实例化其中一个子类。
tf.train.Optimizer
tf.train.GradientDescentOptimizer
tf.train.AdadeltaOptimizer
tf.train.AdagradOptimizer
tf.train.AdagradDAOptimizer
tf.train.MomentumOptimizer
tf.train.AdamOptimizer
tf.train.FtrlOptimizer
tf.train.ProximalGradientDescentOptimizer
tf.train.ProximalAdagradOptimizer
tf.train.RMSPropOptimizer
请参阅tf.contrib.opt更多优化器。