图像反卷积Deconvolution的实现

关于图像反卷积，有很多种说法，下面转一篇觉得好理解且正确的解释。

另附两个链接：

1、 C onvolution arithmetic tutorial

2、Convolution arithmetric github

作者：张骞晖

链接：https://www.zhihu.com/question/43609045/answer/130868981
来源：知乎
著作权归作者所有，转载请联系作者获得授权。

卷积(convolution):
卷积核为 3x3；no padding , strides=1
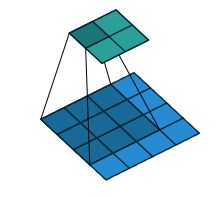反卷积可以理解为upsample conv. "反卷积"(the transpose of conv) 可以理解为upsample conv.
卷积核为:3x3; no padding , strides=1

那看下strides=2的时候。
卷积:


反卷积:

在实际计算过程中，我们要转化为矩阵的乘积的形式，一个转化为
Toeplitz matrix一个reshape为列矩阵。

举个简单的例子

比如 input= [3,3],Reshape之后，为A=[1,9]
B(可以理解为滤波器)=[9,4](Toeplitz matrix)
那么
A*B=C=[1,4]。Reshape C=[2，2]

所以，通过B 卷积，我们从shape=[3,3]变成了shape=[2,2]

反过来。
输入A=[2,2],reshape之后为[1,4]
B的转置为，[4,9]
那么
A*B=C=[1,9],reshape为[3,3]

所以，通过B的转置 - "反卷积"，我们从shape=[2,2]得到了shape=[3,3]

也就是
输入feature map A=[3,3]经过了卷积滤波B=[2,2] 输出为 [2,2] ,所以padding=0,stride=1

反卷积则是
输入feature map A=[2,2],经过了反卷积滤波B=[2,2].输出为[3,3].padding=0,stride=1

那么[2,2]的卷积核(滤波器)是怎么转化为[4,9]或者[9,4]的呢

通过
Toeplitz matrix

不懂的，自己查吧。

所以所谓的卷积其实是转置卷积。

那为什么不能叫反卷积？

反卷积的数学含义，通过反卷积可以将通过卷积的输出信号，完全还原输入信号。

而事实是，转置卷积只能还原shape大小，不能还原value.

你可以自己通过代码验证下。