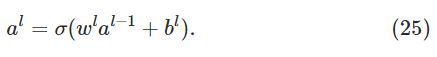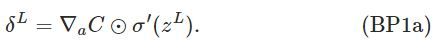神经网络和深度学习（二）——BP(Backpropagation Algorithm, 反向传播算法)

           上一周主要看了 Neural Networks and Deep Learning  网上在线课程的第二章的内容 和 斯坦福大学 《机器学习》的公开课，学习了BP( Back Propagation Algorithm, 反向传播算法)。现在总结如下：

       只要使用神经网络就会用到BP算法，反向传播算法可以用来学习神经网络的权值，仍然采用梯度下降算法，以最小化网络的实际输出与目标输出之间的平方误差为目标。BP算法的目标是在神经网络中可以求任意权值w 和 偏置b 的成本函数（cost function）C 的两个偏导数——C对w的偏导数 和 C对b的偏导数

     首先定义几个符号：

     

图1  的定义

       同样的，再定义  和  ：

      ，    

      

       由此，可以得到激励函数a的计算公式：

     

      公式简写如下：

 

    令 ，则   。

      在正式介绍BP算法之前，先介绍一种运算规则——Hadamard product(阿达马乘积)

      

     

    定义  ：

    根据公式 （23）、（29）可知，the error 是和C对w的偏导数 和 C对b的偏导数 有关。

     现在给出BP算法使用的四个基本公式：

  

    将（BP1）公式改写为矩阵形式的公式：

    关于两层之间的delt计算公式：

     关于偏置b 的BP公式：

        

       上述公式简记为：

      

        关于权值w 的BP公式：

        

     上述公式简记为：

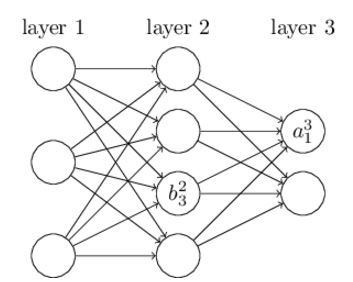
      可以用下图来形象地表示上述关系式

 

       

         有关上述四个公式的证明，这里就不再给出，如果感兴趣可以点击本文开头提供的网上在线课程的链接进行查看，主要就是运用了高数中的链式求导法则进行相关证明。

        BP算法

       BP(反向传播)算法提供了一种计算成本函数（cost function）梯度的方法。算法主要流程如下：

      BP算法的代码实现

   

class Network(object):
...
    def update_mini_batch(self, mini_batch, eta):
        """Update the network's weights and biases by applying
        gradient descent using backpropagation to a single mini batch.
        The "mini_batch" is a list of tuples "(x, y)", and "eta"
        is the learning rate."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        for x, y in mini_batch:
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)     #使用BP算法求解两个偏导数，进而可求成本函数的梯度
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
        self.weights = [w-(eta/len(mini_batch))*nw 
                        for w, nw in zip(self.weights, nabla_w)]
        self.biases = [b-(eta/len(mini_batch))*nb 
                       for b, nb in zip(self.biases, nabla_b)]

            反向传播算法的代码实现：

class Network(object):
...
   def backprop(self, x, y):
        """Return a tuple "(nabla_b, nabla_w)" representing the
        gradient for the cost function C_x.  "nabla_b" and
        "nabla_w" are layer-by-layer lists of numpy arrays, similar
        to "self.biases" and "self.weights"."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # feedforward
        activation = x
        activations = [x] # list to store all the activations, layer by layer
        zs = [] # list to store all the z vectors, layer by layer
        for b, w in zip(self.biases, self.weights):
            z = np.dot(w, activation)+b
            zs.append(z)
            activation = sigmoid(z)
            activations.append(activation)
        # backward pass
        delta = self.cost_derivative(activations[-1], y) * \
            sigmoid_prime(zs[-1])
        nabla_b[-1] = delta
        nabla_w[-1] = np.dot(delta, activations[-2].transpose())
        # Note that the variable l in the loop below is used a little
        # differently to the notation in Chapter 2 of the book.  Here,
        # l = 1 means the last layer of neurons, l = 2 is the
        # second-last layer, and so on.  It's a renumbering of the
        # scheme in the book, used here to take advantage of the fact
        # that Python can use negative indices in lists.
        for l in xrange(2, self.num_layers):
            z = zs[-l]
            sp = sigmoid_prime(z)
            delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
            nabla_b[-l] = delta
            nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
        return (nabla_b, nabla_w)

...

    def cost_derivative(self, output_activations, y):
        """Return the vector of partial derivatives \partial C_x /
        \partial a for the output activations."""
        return (output_activations-y) 

def sigmoid(z):
    """The sigmoid function."""
    return 1.0/(1.0+np.exp(-z))

def sigmoid_prime(z):
    """Derivative of the sigmoid function."""
    return sigmoid(z)*(1-sigmoid(z))