数据结构::矩阵（二）--稀疏矩阵

【稀疏矩阵】：

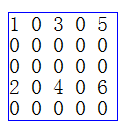
定义：在N*N的矩阵中有效值的个数远小于无效值的个数，且这些数据的分布没有规律（下面这张图就是稀疏矩阵的一个例子：）

【稀疏矩阵的压缩存储】：

   1）稀疏矩阵的存储：压缩存储值存储极少数的有效数据。使用{row,col,value}三元组存储每一个有效数据，三元组按原矩阵中的位置，以行优先级先后顺序依次存放。

template
struct Tripe
{
	Tripe()
	{}   //为resize()的第二个参数创建
	Tripe(const T& x,size_t row,size_t col)
		:_value(x)
		,_row(row)
		,_col(col)
	{}
	T _value;   
	size_t _row;
	size_t _col;
};

接下来我们就将这个三元组存储在数组里，因为我们在开辟一个空间的时候，我们并不知道要开多大，会造成很不方便，所以这里我们就用vector来进行存储，在存储的时候直接调用尾插。

template
class SparseMatrix
{
public:
	//构造函数
	SparseMatrix()
	{}
	
	SparseMatrix(T* a,size_t m,size_t n,const T& invalue)
		:_a()
		,_rowSize(m)
		,_colSize(n)
		,_invalue(invalue)
	{
		for(size_t i = 0; itemp(a[i*n+j],i,j);//先创建一个三元组的变量来存储你要放入矩阵里的数组元素
					_a.push_back(temp);  //再调用vector里的尾插进行压栈
				}
			}
		}
	}
private:
	vector> _a;
	size_t _rowSize;
	size_t _colSize;
	T _invalue;     //存储无用值
};

2）稀疏矩阵的打印：这块的打印是与构造函数相对应的，因此在我们打印的时候可以一行一行的进行遍历，如果此行和列分别对应等于当前元素的行和列，那么就打印出当前有效值，否则就打印出0这个无效值。

//打印三元组
	void Printp()
	{
		for(size_t i = 0; i<_a.size(); i++)
		{
			cout<<"col: "<<_a[i]._col
				<<"row: "<<_a[i]._row
				<<"value; "<<_a[i]._value<

【稀疏矩阵的转置】：

1、定义：将原矩阵的行列交换,也就是将[i][j]和[j][i]的位置互换（如下图:）

2、稀疏矩阵的转置的方式：

1）普通转置：

     【原理说明】：原来的列是转置之后的行，因此我们要得到转置之后的矩阵，就要对原来的矩阵进行一列一列的遍历，即就是外层列的循环，内层进行vector的尾插，不断插入元素即可。

SparseMatrix Tranport()
	{
		//先创建转置后的数组
		size_t index = 0;
		SparseMatrix sm;
		sm._rowSize = _colSize;//现在的行是原来的列
		sm._colSize = _rowSize;//现在的列是原来的行
		sm._invalue = _invalue;//无效值不变
		sm._a.reserve(_a.size());//是优化，首先开辟的是size大小；其次在Push_back的时候不会再去扩容了
		//开始从列查找
		for(size_t i = 0; i<_colSize; i++)
		{
			//遍历原来的整个容器
			for(size_t index = 0; index <_a.size(); index++)
			{
				if(_a[index]._col == i)
				{
					Tripe temp(_a[index]._value,_a[index]._col,_a[index]._row);
					sm._a.push_back(temp);
				}
			}
		}
		return sm;
	}

2）快速转置：在我们上面的普通转置中时间复杂度是O（稀疏矩阵的列*稀疏矩阵的元素个数），这个确实是很慢的，那我们可不可以进行优化，找到这个位置后直接将其定位到压缩矩阵中本该属于它的位置，由此引入了快速转置。

   【原理说明】：如果我们知道转置之后的每一行的有效元素的个数和转置之后每一行中的元素的起始位置，这样的话我们将两者结合起来就可以进行稀疏矩阵的快速转置了

    A:我们开两个数组：一个数组是用来记录转置之后每一行的有效元素的个数，一个数组是用来记录转置之后的元素在压缩矩阵中的起始位置。开的大小就是转置之前列的数目。

    B：记录转置之后每一行的有效元素的个数的获取：我们要将矩阵进行遍历一遍，对应的列数加在对应的count数组中，记得memset

    C：记录转置之后的元素在压缩矩阵中的起始位置的获取：第一个元素一定是0，后面的元素的起始位置就是上一个元素的起始位置+上一个元素的个数

    D:最后我们就将矩阵中的元素放到它的对应位置

SparseMatrix FastTranport()
	{
		SparseMatrix sm;
		sm._rowSize = _colSize;
		sm._colSize = _rowSize;
		sm._invalue = _invalue;
		//统计转置后矩阵每一行的个数
		int* count = new int[_colSize];
		memset(count,0,sizeof(int)*_colSize);
		//统计转置后的矩阵在每行压缩矩阵中存储的开始位置
		int* start = new int[_colSize];
		sm._a.resize(_a.size());   //下面是用下标访问的，用resize会比较合适
		size_t index = 0;
		while(index < _a.size())
		{
			count[_a[index]._col]++; //用原来列的有效数值位作为计数的下标
			++index;
		}
		start[0] = 0; //第一个数值一定是0
		for(size_t i = 1; i<_colSize; i++)
		{
			start[i] = start[i-1]+count[i-1];
		}
		index = 0;
		while(index<_a.size())
		{
			Tripetemp(_a[index]._value,_a[index]._col,_a[index]._row);
			sm._a[start[_a[index]._col]++] = temp;
			++index;
		}
		delete[]count;
		delete[]start;
		return sm;
	}