线性判别分析简明入门教程

原文：http://sebastianraschka.com/Articles/2014_python_lda.html
编译：Asher Li

注1：文中出现了线性代数术语“eigenvalue”“eigenvector”，中文教材对应有“特征值”“本征值”两种常见译法。为了与“feature”相区分，本文使用“本征”翻译。

注2：文中提到 “ k×d -维本征向量矩阵”，原文写作 “ k×d -dimensional eigenvector matrix”，指的是“k个d维的本征向量组成的矩阵”。
中文与公式混合排版之后可能引发歧义，故在此做单独解释。

导语

在模式分类和机器学习实践中，线性判别分析（Linear Discriminant Analysis, LDA）方法常被用于数据预处理中的降维（dimensionality reduction）步骤。LDA在保证良好的类别区分度的前提下，将数据集向更低维空间投影，以求在避免过拟合（“维数灾难”）的同时，减小计算消耗。

Ronald A. Fisher 在1936年（The Use of Multiple Measurements in Taxonomic Problems）提出了线性判别（Linear Discriminant）方法，它有时也用来解决分类问题。最初的线性判别适用于二分类问题，后来在1948年，被C. R. Rao（The utilization of multiple measurements in problems of biological classification）推广为“多类线性判别分析”或“多重判别分析”。

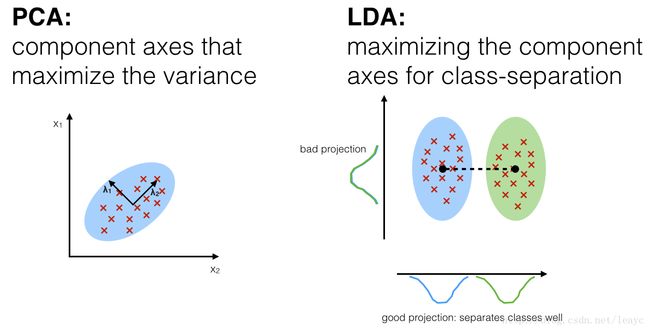
一般意义上的LDA与主成分分析（Principal Component Analysis，PCA）十分相似，但不同于PCA寻找使全部数据方差最大化的坐标轴成分，LDA关心的是能够最大化类间区分度的坐标轴成分。

更多关于PCA的内容，可参考 Implementing a Principal Component Analysis (PCA) in Python step by step。

一言蔽之，LDA将特征空间（数据集中的多维样本）投影到一个维度更小的 k 维子空间中（ k≤n−1 ），同时保持区分类别的信息。
通常情况下，降维不仅降低了分类任务的计算量，还能减小参数估计的误差，从而避免过拟合。

主成分分析 vs. 线性判别分析

线性判别分析（LDA）与主成分分析（PCA）都是常用的线性变换降维方法。PCA是一种“无监督”算法，它不关心类别标签，而是致力于寻找数据集中最大化方差的那些方向（亦即“主成分”）；LDA则是“有监督”的，它计算的是另一类特定的方向（或称线性判别“器”）——这些方向刻画了最大化类间区分度的坐标轴。

虽然直觉上听起来，在已知类别信息时，LDA对于多分类任务要优于PCA，但实际并不一定。
比如比较经过PCA或LDA处理后图像识别任务的分类准确率，如果样本数比较少，PCA是要优于LDA的（PCA vs. LDA, A.M. Martinez et al., 2001）。联合使用LDA和PCA也并不罕见，例如降维时先用PCA再做LDA。

什么是“好”的特征子空间

假定我们的目标是将一个 d 维数据集投影到一个 k （ k<d ）维子空间中从而降低它的维度，我们怎么知道该选择多大的 k 呢？我们又怎么知道这个特征空间是否能很“好”地表达我们的数据呢？

在后面，我们会计算数据集的本征向量（成分），将其归总到一个所谓的“散布矩阵”（类间散布矩阵和类内散布矩阵）。每一个本征向量对应一个本征值，本征值会告诉我们相应本征向量的“长度”/“大小”。

如果所有的本征值大小都很相近，那么这就表示我们的数据已经投影到了一个“好”的特征空间上。
而如果一部分本征值远大于其他的本征值，我们可能就考虑只留下最大的那些，因为它们包含了更多关于数据的分布的信息。反之，接近 0 的本征值含有的信息量更少，我们就考虑在构造新特征空间时舍弃它们。

LDA的五个步骤

下面列出了执行线性判别分析的五个基本步骤。我们会在后面做更详细的讲解。
 1. 计算数据集中不同类别数据的 d 维均值向量。
 2. 计算散布矩阵，包括类间、类内散布矩阵。
 3. 计算散布矩阵的本征向量 e1,e2,...,ed 和对应的本征值 λ1,λ2,...,λd 。
 4. 将本征向量按本征值大小降序排列，然后选择前 k 。 个最大本征值对应的本征向量，组建一个 d×k 维矩阵——即每一列就是一个本征向量。
 5. 用这个 d×k -维本征向量矩阵将样本变换到新的子空间。这一步可以写作矩阵乘法 Y=X×W 。 X 是 n×d 维矩阵，表示 n 个样本； y 是变换到子空间后的 n×k 维样本。

准备样本数据集

鸢尾花集

接下来要在著名的“鸢尾花”数据集上折腾一番。鸢尾花集可从UCI的机器学习目录中下载：
https://archive.ics.uci.edu/ml/datasets/Iris
引用: Bache, K. & Lichman, M. (2013). UCI Machine Learning Repository. Irvine, CA: University of California, School of Information and Computer Science.

该集对三类、一百五十朵鸢尾花做了测量。

三类包括：
 1. 山鸢尾（n=50）
 2. 变色鸢尾（n=50）
 3. 维吉尼亚鸢尾（n=50）
四种特征包括：
 1. 萼片长度（厘米）
 2. 萼片宽度（厘米）
 3. 花瓣长度（厘米）
 4. 花瓣宽度（厘米）

feature_dict = {i:label for i,label in zip(
                range(4),
                  ('sepal length in cm',
                  'sepal width in cm',
                  'petal length in cm',
                  'petal width in cm', ))}

读取数据集

import pandas as pd

df = pd.io.parsers.read_csv(
    filepath_or_buffer='https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data',
    header=None,
    sep=',',
    )
df.columns = [l for i,l in sorted(feature_dict.items())] + ['class label']
df.dropna(how="all", inplace=True) # to drop the empty line at file-end

df.tail()

	sepal length in cm	sepal width in cm	petal length in cm	pedal width in cm	class label
145	6.7	3.0	5.2	2.3	Iris-virginica
146	6.3	2.5	5.0	1.9	Iris-virginaica
147	6.5	3.0	5.2	2.0	Iris-virginaica
148	6.2	3.4	5.4	2.3	Iris-virginaica
149	5.9	3.0	5.1	1.8	Iris-virginaica

XX=⎡⎣⎢⎢⎢⎢x1sepal lengthx2sepal length...x150sepal lengthx1sepal widthx2sepal widthx150sepal widthx1petal lengthx2petal lengthx150petal lengthx1petal widthx2petal widthx150petal width⎤⎦⎥⎥⎥⎥,yy=⎡⎣⎢⎢⎢⎢ωsetosaωsetosa...ωvirginica⎤⎦⎥⎥⎥⎥

因为数值数据更容易处理，我们使用 scikit-learn 库中的 LabelEncode 将类别标签转换成数字 1，2，3：

from sklearn.preprocessing import LabelEncoder

X = df[[0,1,2,3]].values
y = df['class label'].values

enc = LabelEncoder()
label_encoder = enc.fit(y)
y = label_encoder.transform(y) + 1

label_dict = {1: 'Setosa', 2: 'Versicolor', 3:'Virginica'}

yy=⎡⎣⎢⎢⎢setosasetosa...virginica⎤⎦⎥⎥⎥⇒⎡⎣⎢⎢⎢11...3⎤⎦⎥⎥⎥

直方图和特征选择

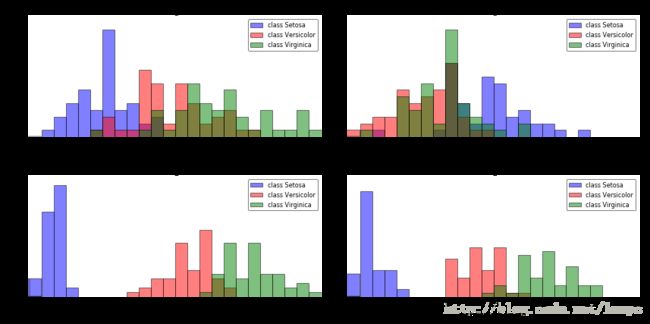
把四种特征的分布情况在一维直方图中分别做可视化呈现，可以得到一个对 w1,w2,w3 三类数据的粗略的观察：

%matplotlib inline

from matplotlib import pyplot as plt
import numpy as np
import math

fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(12,6))

for ax,cnt in zip(axes.ravel(), range(4)):  

    # set bin sizes
    min_b = math.floor(np.min(X[:,cnt]))
    max_b = math.ceil(np.max(X[:,cnt]))
    bins = np.linspace(min_b, max_b, 25)

    # plottling the histograms
    for lab,col in zip(range(1,4), ('blue', 'red', 'green')):
        ax.hist(X[y==lab, cnt],
                   color=col,
                   label='class %s' %label_dict[lab],
                   bins=bins,
                   alpha=0.5,)
    ylims = ax.get_ylim()

    # plot annotation
    leg = ax.legend(loc='upper right', fancybox=True, fontsize=8)
    leg.get_frame().set_alpha(0.5)
    ax.set_ylim([0, max(ylims)+2])
    ax.set_xlabel(feature_dict[cnt])
    ax.set_title('Iris histogram #%s' %str(cnt+1))

    # hide axis ticks
    ax.tick_params(axis="both", which="both", bottom="off", top="off",  
            labelbottom="on", left="off", right="off", labelleft="on")

    # remove axis spines
    ax.spines["top"].set_visible(False)  
    ax.spines["right"].set_visible(False)
    ax.spines["bottom"].set_visible(False)
    ax.spines["left"].set_visible(False)    

axes[0][0].set_ylabel('count')
axes[1][0].set_ylabel('count')

fig.tight_layout()       

plt.show()

仅凭这些简单的图形化展示，已经足以让我们得出结论：在四种特征里面，花瓣的长度、宽度更适合用来区分三种鸢尾花类别。
实际应用中，比起通过投影降维（此处即LDA），另一种比较好的办法是做特征筛选。像鸢尾花这样的低维数据集，看一眼直方图就能得到很多信息了。
另一种简单但有效的方式是使用特征选择算法——如果你有兴趣，我在此处详述了“序列特征选择”； scikit-learn 有另一种漂亮的手段。
我还写过一篇“特征选择中的滤波器，封装器和嵌入方法”，是在更高的层次上对不同方法的总结。

规范性假设

需要指出，LDA假设数据服从正态分布、不同特征之间互相统计独立且各类数据的协方差矩阵相等。不过这仅仅指LDA用作分类器的情况，当LDA用于降维时，哪怕数据不符合这些假设，LDA通常也能取得不错的效果。
而即便对于分类任务，LDA对数据的分布似乎也是相当鲁棒的：

“尽管实际情况常常不符合‘不同类别数据间有相同协方差矩阵’和规范性假设，线性判别分析在人脸和物体识别任务中也通常能够得到不错的结果。”。

Tao Li, Shenghuo Zhu, and Mitsunori Ogihara. “Using Discriminant Analysis for Multi-Class Classification: An Experimental Investigation.” Knowledge and Information Systems 10, no. 4 (2006): 453–72.)
Duda, Richard O, Peter E Hart, and David G Stork. 2001. Pattern Classification. New York: Wiley.

五步实现LDA

完成以上几项准备工作后，我们就可以实际运行LDA了。

第一步：计算数据的 d 维均值向量

首先做一个简单的计算：分别求三种鸢尾花数据在不同特征维度上的均值向量 mi ：

mmi=⎡⎣⎢⎢⎢⎢⎢μωi(sepal length)μωi(sepal width)μωi(petal length)μωi(petal width)⎤⎦⎥⎥⎥⎥⎥,withi=1,2,3

np.set_printoptions(precision=4)

mean_vectors = []
for cl in range(1,4):
    mean_vectors.append(np.mean(X[y==cl], axis=0))
    print('Mean Vector class %s: %s\n' %(cl, mean_vectors[cl-1]))

得到

Mean Vector class 1: [ 5.006  3.418  1.464  0.244]

Mean Vector class 2: [ 5.936  2.77   4.26   1.326]

Mean Vector class 3: [ 6.588  2.974  5.552  2.026]

第二步：计算散布矩阵

计算两个 4×4 维矩阵：类内散布矩阵和类间散布矩阵。

2.1a 类内散布矩阵 Sw

类内散布矩阵 Sw 由该式算出：

SW=∑i=1cSi

其中
Si=∑xx∈Din(xx−mmi)(xx−mmi)T,

mmi=1ni∑xx∈Dinxxk

S_W = np.zeros((4,4))
for cl,mv in zip(range(1,4), mean_vectors):
    class_sc_mat = np.zeros((4,4))                  # scatter matrix for every class
    for row in X[y == cl]:
        row, mv = row.reshape(4,1), mv.reshape(4,1) # make column vectors
        class_sc_mat += (row-mv).dot((row-mv).T)
    S_W += class_sc_mat                             # sum class scatter matrices
print('within-class Scatter Matrix:\n', S_W)

得到

within-class Scatter Matrix:
 [[ 38.9562  13.683   24.614    5.6556]
 [ 13.683   17.035    8.12     4.9132]
 [ 24.614    8.12    27.22     6.2536]
 [  5.6556   4.9132   6.2536   6.1756]]

2.1b 贝塞尔纠偏项的影响

在计算类-协方差矩阵时，可以在类内散布矩阵上添加尺度因数 1N−1 ，这样计算式就变为

Σi=1Ni−1∑xx∈Din(xx−mmi)(xx−mmi)T

SW=∑i=1c(Ni−1)Σi

Ni 是类样本大小（此处为50），因为三个类别的样本数是相同的，这里可以舍去 (Ni−1) 。
因为本征向量是相同的，只是本征值有一个常数项的尺度变化，所以即便将其忽略不计，最后得到的特征空间也不会改变（这一点在文末还有体现）。

2.2 类间散布矩阵 SB

计算类间散布矩阵 SB ：

SB=∑i=1cNi(mmi−mm)(mmi−mm)T

mm 是全局均值，而 mmi 和 Ni 是每类样本的均值和样本数。

overall_mean = np.mean(X, axis=0)

S_B = np.zeros((4,4))
for i,mean_vec in enumerate(mean_vectors):  
    n = X[y==i+1,:].shape[0]
    mean_vec = mean_vec.reshape(4,1) # make column vector
    overall_mean = overall_mean.reshape(4,1) # make column vector
    S_B += n * (mean_vec - overall_mean).dot((mean_vec - overall_mean).T)

print('between-class Scatter Matrix:\n', S_B)

得到

between-class Scatter Matrix:
 [[  63.2121  -19.534   165.1647   71.3631]
 [ -19.534    10.9776  -56.0552  -22.4924]
 [ 165.1647  -56.0552  436.6437  186.9081]
 [  71.3631  -22.4924  186.9081   80.6041]]

第三步：求解矩阵 S−1WSB 的广义本征值

接下来求解矩阵 S−1WSB 的广义本征值问题，从而得到线性判别“器”：

eig_vals, eig_vecs = np.linalg.eig(np.linalg.inv(S_W).dot(S_B))

for i in range(len(eig_vals)):
    eigvec_sc = eig_vecs[:,i].reshape(4,1)   
    print('\nEigenvector {}: \n{}'.format(i+1, eigvec_sc.real))
    print('Eigenvalue {:}: {:.2e}'.format(i+1, eig_vals[i].real))

得到

Eigenvector 1:
[[-0.2049]
 [-0.3871]
 [ 0.5465]
 [ 0.7138]]
Eigenvalue 1: 3.23e+01

Eigenvector 2:
[[-0.009 ]
 [-0.589 ]
 [ 0.2543]
 [-0.767 ]]
Eigenvalue 2: 2.78e-01

Eigenvector 3:
[[ 0.179 ]
 [-0.3178]
 [-0.3658]
 [ 0.6011]]
Eigenvalue 3: -4.02e-17

Eigenvector 4:
[[ 0.179 ]
 [-0.3178]
 [-0.3658]
 [ 0.6011]]
Eigenvalue 4: -4.02e-17

计算结果应当作何解释呢？从第一节线性代数课开始我们就知道，本征向量和本征值表示了一个线性变换的形变程度——本征向量是形变的方向；本征值是本征向量的尺度因数，刻画了形变的幅度。
如果将LDA用于降维，本征向量非常重要，因为它们将会组成新特征子空间的坐标轴。对应的本征值表示了这些新坐标轴的信息量的多少。

再检查一遍计算过程，然后对本征值做进一步讨论。

检查本征向量-本征值的运算

要检查该运算是否正确，看其是否满足等式：

AvAv=λvλv

此处
AA=S−1WSB

vv:Eigenvector

λλ:Eigenvalue

for i in range(len(eig_vals)):
    eigv = eig_vecs[:,i].reshape(4,1)
    np.testing.assert_array_almost_equal(np.linalg.inv(S_W).dot(S_B).dot(eigv),
                                         eig_vals[i] * eigv,
                                         decimal=6, err_msg='', verbose=True)
print('ok')

输出：

ok

第四步：选择线性判别“器”构成新的特征子空间

4.1 按本征值降序排列本征向量

本征向量只是定义了新坐标轴的方向，它们的大小都是单位长度1。

想要构成更低维的子空间，就得选择丢弃哪个（些）本征向量，所以我们得看看对应本征向量的那些本征值。 大体上说，对于数据的分布情况，本征值最小的那些本征向量所承载的信息最少，所以要舍弃的就是这些本征向量。
将本征向量根据本征值的大小从高到低排序，然后选择前 k 个本征向量：

# Make a list of (eigenvalue, eigenvector) tuples
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]

# Sort the (eigenvalue, eigenvector) tuples from high to low
eig_pairs = sorted(eig_pairs, key=lambda k: k[0], reverse=True)

# Visually confirm that the list is correctly sorted by decreasing eigenvalues

print('Eigenvalues in decreasing order:\n')
for i in eig_pairs:
    print(i[0])

得到

Eigenvalues in decreasing order:

32.2719577997
0.27756686384
5.71450476746e-15
5.71450476746e-15

可以看到有两个本征值接近0，不是因为它们不含信息量，而是浮点数精度的关系。其实，这后两个本征值应该恰好为0。
在LDA中，线性判别器的数目最多是 c−1 ， c 是总的类别数，这是因为类内散布矩阵 SB 是 c 个秩为1或0的矩阵的和。
注意到很少有完全共线的情况（所有样本点分布在一条直线上），协方差矩阵秩为1，这导致了只有一个非零本征值和一个对应的本征向量。
现在，把“可释方差”表达为百分数的形式：

print('Variance explained:\n')
eigv_sum = sum(eig_vals)
for i,j in enumerate(eig_pairs):
    print('eigenvalue {0:}: {1:.2%}'.format(i+1, (j[0]/eigv_sum).real))

得到

Variance explained:

eigenvalue 1: 99.15%
eigenvalue 2: 0.85%
eigenvalue 3: 0.00%
eigenvalue 4: 0.00%

第一个本征对是信息量最大的一组，如果我们考虑建立一个一维的向量空间，使用该本征对就不会丢失太多信息。

4.2 选择 k 个最大本征值对应的本征向量

按本征值的大小得到降序排列的本征对之后，现在就可以组建我们的 k×d -维本征向量矩阵 W 了（此时大小为 4×2 ），这样就从最初的4维特征空间降到了2维的特征空间。

W = np.hstack((eig_pairs[0][1].reshape(4,1), eig_pairs[1][1].reshape(4,1)))
print('Matrix W:\n', W.real)

得到

Matrix W:
 [[-0.2049 -0.009 ]
 [-0.3871 -0.589 ]
 [ 0.5465  0.2543]
 [ 0.7138 -0.767 ]]

第五步：将样本变换到新的子空间中

使用上一步刚刚计算出的 4×2 -维矩阵 W ， 将样本变换到新的特征空间上：

YY=XX×WW

其中 XX 是一个 n×d 维矩阵，表示 n 个样本， YY 是变换后新子空间中的 n×k 维样本。

X_lda = X.dot(W)
assert X_lda.shape == (150,2), "The matrix is not 150x2 dimensional."

得到

from matplotlib import pyplot as plt

def plot_step_lda():

    ax = plt.subplot(111)
    for label,marker,color in zip(
        range(1,4),('^', 's', 'o'),('blue', 'red', 'green')):

        plt.scatter(x=X_lda[:,0].real[y == label],
                y=X_lda[:,1].real[y == label],
                marker=marker,
                color=color,
                alpha=0.5,
                label=label_dict[label]
                )

    plt.xlabel('LD1')
    plt.ylabel('LD2')

    leg = plt.legend(loc='upper right', fancybox=True)
    leg.get_frame().set_alpha(0.5)
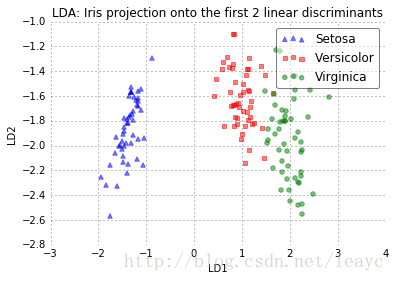
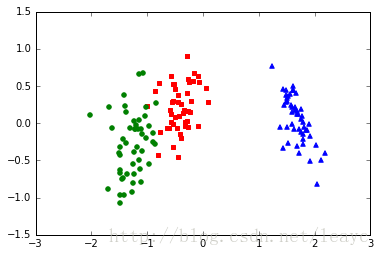
    plt.title('LDA: Iris projection onto the first 2 linear discriminants')

    # hide axis ticks
    plt.tick_params(axis="both", which="both", bottom="off", top="off",  
            labelbottom="on", left="off", right="off", labelleft="on")

    # remove axis spines
    ax.spines["top"].set_visible(False)  
    ax.spines["right"].set_visible(False)
    ax.spines["bottom"].set_visible(False)
    ax.spines["left"].set_visible(False)    

    plt.grid()
    plt.tight_layout
    plt.show()

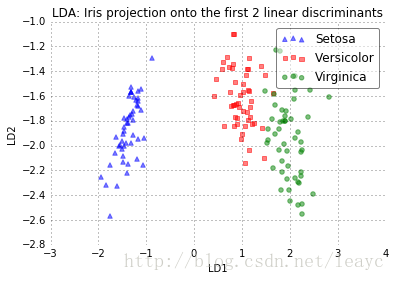
plot_step_lda()

上方散点图展示了我们通过 LDA 构建的新的特征子空间。可以看到第一个线性判别器“LD1”把不同类数据区分得不错，第二个线性判别器就不行了。其原因在上面已经做了简单解释。

PCA 和 LDA 的对比

为了与使用线性判别分析得到的特征子空间作比较，我们将使用 scikit-learn 机器学习库中的 PCA 类。文档看这里：http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html。
方便起见，我们直接在 n_components 参数上设定了希望从输入数据集中得到的成分数量。

n_components : int, None or string

Number of components to keep. if n_components is not set all components are kept:
    n_components == min(n_samples, n_features)
    if n_components == ‘mle’, Minka’s MLE is used to guess the dimension if 0 < n_components < 1,
    select the number of components such that the amount of variance that needs to be explained
    is greater than the percentage specified by n_components

但是在观察两种线性变换的结果之前，让我们快速复习一下 PCA 和 LDA 的目标：PCA 在整个数据集中寻找方差最大的坐标轴，而 LDA 则寻找对于类别区分度最佳的坐标轴。
实际的降维步骤中，经常是LDA放在PCA之后使用。

from sklearn.decomposition import PCA as sklearnPCA

sklearn_pca = sklearnPCA(n_components=2)
X_pca = sklearn_pca.fit_transform(X)

def plot_pca():

    ax = plt.subplot(111)

    for label,marker,color in zip(
        range(1,4),('^', 's', 'o'),('blue', 'red', 'green')):

        plt.scatter(x=X_pca[:,0][y == label],
                y=X_pca[:,1][y == label],
                marker=marker,
                color=color,
                alpha=0.5,
                label=label_dict[label]
                )

    plt.xlabel('PC1')
    plt.ylabel('PC2')

    leg = plt.legend(loc='upper right', fancybox=True)
    leg.get_frame().set_alpha(0.5)
    plt.title('PCA: Iris projection onto the first 2 principal components')

    # hide axis ticks
    plt.tick_params(axis="both", which="both", bottom="off", top="off",  
            labelbottom="on", left="off", right="off", labelleft="on")

    # remove axis spines
    ax.spines["top"].set_visible(False)  
    ax.spines["right"].set_visible(False)


    ax.spines["bottom"].set_visible(False)
    ax.spines["left"].set_visible(False)    

    plt.tight_layout
    plt.grid()

    plt.show()

然后执行

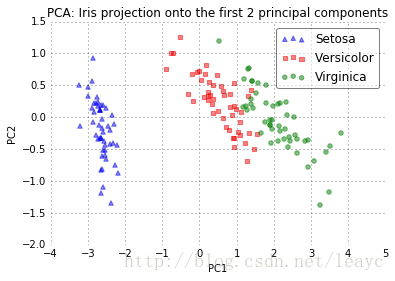
plot_pca()
plot_step_lda()

回想我们之前讨论的内容：PCA 获取数据集中方差最大的成分，而LDA给出不同类别间方差最大的坐标轴。

使用 scikit-learn 中的 LDA

我们已经看到，线性判别分析是如何一步步实现的了。其实通过使用 scikit-learn
机器学习库中的 LDA ，我们可以更方便地实现同样的结果。

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA

# LDA
sklearn_lda = LDA(n_components=2)
X_lda_sklearn = sklearn_lda.fit_transform(X, y)

作图：

def plot_scikit_lda(X, title):

    ax = plt.subplot(111)
    for label,marker,color in zip(
        range(1,4),('^', 's', 'o'),('blue', 'red', 'green')):

        plt.scatter(x=X[:,0][y == label],
                    y=X[:,1][y == label] * -1, # flip the figure
                    marker=marker,
                    color=color,
                    alpha=0.5,
                    label=label_dict[label])

    plt.xlabel('LD1')
    plt.ylabel('LD2')

    leg = plt.legend(loc='upper right', fancybox=True)
    leg.get_frame().set_alpha(0.5)
    plt.title(title)

    # hide axis ticks
    plt.tick_params(axis="both", which="both", bottom="off", top="off",  
            labelbottom="on", left="off", right="off", labelleft="on")

    # remove axis spines
    ax.spines["top"].set_visible(False)  
    ax.spines["right"].set_visible(False)
    ax.spines["bottom"].set_visible(False)
    ax.spines["left"].set_visible(False)    

    plt.grid()
    plt.tight_layout
    plt.show()

执行

plot_step_lda()
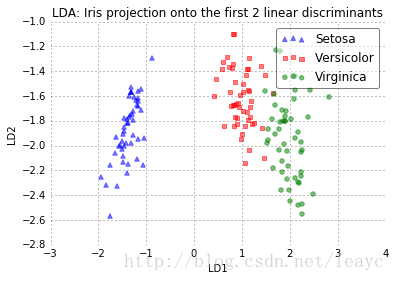
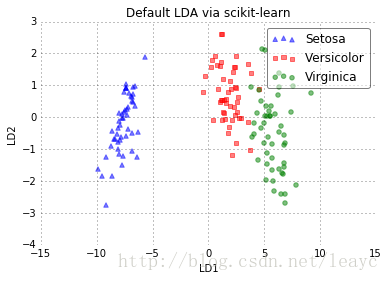
plot_scikit_lda(X_lda_sklearn, title='Default LDA via scikit-learn')

关于规范化

最近被问到了这个问题，所以我做一下说明：对特征做尺度变换，比如【规范化】，不会改变LDA的最终结果，所以这是可选步骤。的确，散布矩阵会因为特征的缩放而发生变化，而且本征向量也因此而改变。但是关键的部分在于，最终本征值不会变——唯一可见的不同只是成分轴的尺度大小。这在数学上是可以证明的（将来我可能在这儿插入一些公式）。

%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt

import pandas as pd

df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=None)
df[4] = df[4].map({'Iris-setosa':0, 'Iris-versicolor':1, 'Iris-virginica':2})
df.tail()

	sepal length in cm	sepal width in cm	petal length in cm	pedal width in cm	class label
145	6.7	3.0	5.2	2.3	Iris-virginica
146	6.3	2.5	5.0	1.9	Iris-virginaica
147	6.5	3.0	5.2	2.0	Iris-virginaica
148	6.2	3.4	5.4	2.3	Iris-virginaica
149	5.9	3.0	5.1	1.8	Iris-virginaica

读取数据集，对 X 中的列做规范化。规范化就是把数据用均值做中心化、用标准差做单位化：

xstd=x−μxσX

这样所有的列就都是 0 均值（ μxstd=0 ）、标准差为 1 的了（\sigma_{x_{std}}=1）。

y, X = df.iloc[:, 4].values, df.iloc[:, 0:4].values
X_cent = X - X.mean(axis=0)
X_std = X_cent / X.std(axis=0)

接下来我简单复制了一下LDA的各个步骤，这些之前我们都讨论过了。为简便都写成了Python函数。

import numpy as np

def comp_mean_vectors(X, y):
    class_labels = np.unique(y)
    n_classes = class_labels.shape[0]
    mean_vectors = []
    for cl in class_labels:
        mean_vectors.append(np.mean(X[y==cl], axis=0))
    return mean_vectors

def scatter_within(X, y):
    class_labels = np.unique(y)
    n_classes = class_labels.shape[0]
    n_features = X.shape[1]
    mean_vectors = comp_mean_vectors(X, y)
    S_W = np.zeros((n_features, n_features))
    for cl, mv in zip(class_labels, mean_vectors):
        class_sc_mat = np.zeros((n_features, n_features))                 
        for row in X[y == cl]:
            row, mv = row.reshape(n_features, 1), mv.reshape(n_features, 1)
            class_sc_mat += (row-mv).dot((row-mv).T)
        S_W += class_sc_mat                           
    return S_W

def scatter_between(X, y):
    overall_mean = np.mean(X, axis=0)
    n_features = X.shape[1]
    mean_vectors = comp_mean_vectors(X, y)    
    S_B = np.zeros((n_features, n_features))
    for i, mean_vec in enumerate(mean_vectors):  
        n = X[y==i+1,:].shape[0]
        mean_vec = mean_vec.reshape(n_features, 1)
        overall_mean = overall_mean.reshape(n_features, 1)
        S_B += n * (mean_vec - overall_mean).dot((mean_vec - overall_mean).T)
    return S_B

def get_components(eig_vals, eig_vecs, n_comp=2):
    n_features = X.shape[1]
    eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
    eig_pairs = sorted(eig_pairs, key=lambda k: k[0], reverse=True)
    W = np.hstack([eig_pairs[i][1].reshape(4, 1) for i in range(0, n_comp)])
    return W

先把还没有做尺度变换的数据的本征值、本征向量和投影矩阵打印出来：

S_W, S_B = scatter_within(X, y), scatter_between(X, y)
eig_vals, eig_vecs = np.linalg.eig(np.linalg.inv(S_W).dot(S_B))
W = get_components(eig_vals, eig_vecs, n_comp=2)
print('EigVals: %s\n\nEigVecs: %s' % (eig_vals, eig_vecs))
print('\nW: %s' % W)

结果：

EigVals: [  2.0905e+01 +0.0000e+00j   1.4283e-01 +0.0000e+00j
  -2.8680e-16 +1.9364e-15j  -2.8680e-16 -1.9364e-15j]

EigVecs: [[ 0.2067+0.j      0.0018+0.j      0.4846-0.4436j  0.4846+0.4436j]
 [ 0.4159+0.j     -0.5626+0.j      0.0599+0.1958j  0.0599-0.1958j]
 [-0.5616+0.j      0.2232+0.j      0.1194+0.1929j  0.1194-0.1929j]
 [-0.6848+0.j     -0.7960+0.j     -0.6892+0.j     -0.6892-0.j    ]]

W: [[ 0.2067+0.j  0.0018+0.j]
 [ 0.4159+0.j -0.5626+0.j]
 [-0.5616+0.j  0.2232+0.j]
 [-0.6848+0.j -0.7960+0.j]]

作图：

X_lda = X.dot(W)
for label,marker,color in zip(
        np.unique(y),('^', 's', 'o'),('blue', 'red', 'green')):
    plt.scatter(X_lda[y==label, 0], X_lda[y==label, 1],
                color=color, marker=marker)

再对规范化之后的数据集重复上述操作：

S_W, S_B = scatter_within(X_std, y), scatter_between(X_std, y)
eig_vals, eig_vecs = np.linalg.eig(np.linalg.inv(S_W).dot(S_B))
W_std = get_components(eig_vals, eig_vecs, n_comp=2)
print('EigVals: %s\n\nEigVecs: %s' % (eig_vals, eig_vecs))
print('\nW: %s' % W_std)

得到

EigVals: [  2.0905e+01   1.4283e-01  -6.7207e-16   1.1082e-15]

EigVecs: [[ 0.1492 -0.0019  0.8194 -0.3704]
 [ 0.1572  0.3193 -0.1382 -0.0884]
 [-0.8635 -0.5155 -0.5078 -0.5106]
 [-0.4554  0.7952 -0.2271  0.7709]]

W: [[ 0.1492 -0.0019]
 [ 0.1572  0.3193]
 [-0.8635 -0.5155]
 [-0.4554  0.7952]]

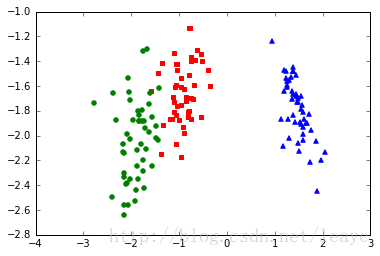
作图：

X_std_lda = X_std.dot(W_std)
X_std_lda[:, 0] = -X_std_lda[:, 0]
X_std_lda[:, 1] = -X_std_lda[:, 1]
for label,marker,color in zip(
        np.unique(y),('^', 's', 'o'),('blue', 'red', 'green')):
    plt.scatter(X_std_lda[y==label, 0], X_std_lda[y==label, 1],
                color=color, marker=marker)

可以看到，不管做不做尺度变化，本征值是一样的（要注意到， W 的秩是2，4维数据集中最小的两个本征值本来就应该是0）。并且，你也看到了，除了成分轴的尺度不太一样，以及图形做了中心对称翻转，最后的投影结果基本没有区别。