t-SNE及pytorch实现
概述
tSNE是一个很流行的降维可视化方法,能在二维平面上把原高维空间数据的自然聚集表现的很好。这里学习下原始论文,然后给出pytoch实现。整理成博客方便以后看
SNE
tSNE是对SNE的一个改进,SNE来自Hinton大佬的早期工作。tSNE也有Hinton的参与。先解释下SNE。
SNE 全称叫Stochastic Neighbor Embedding。思想是这样的,分别在降维前和降维后的数据集上定义一个函数,计算每个点对(i与j)之间的‘距离’。在SNE中,这个距离是非线性的高斯分布,所以SNE是一种非线性降维方法,这也是其相比PCA等线性方法能更加强大的一个核心原因。在SNE里,函数具体如下定义。后面称之为相似度函数好了,这样比较直观


注:pii qii均令为零,因为这里讨论点对之间关系,与自身的没有意义
然后算法的工作就是怼出来最合适的降维,来让降维前后点对之间相似度最接近(即原来远的还远,原来近的还近)。这个前后相似的判别标准SNE里使用了KL散度,比较直观。
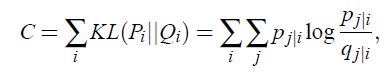
然后这玩意就用SGD之类的train就好了。不过原文提到不大好train,用到了模拟退火之类的方法。
tSNE
全称为t-Distributed Stochastic Neighbor Embedding 做为对SNE的改进,有以下两点
1.解决不对称问题
SNE的相似度函数是条件概率,p(i|j)!=p(j|i),这会导致一个问题:其对原来远的点表达近了这种错误很灵敏,对原来近的表达远了的错误惩罚不佳(从其优化目标KL散度的公式可看出。注意乘的p(j|i)),所以这会令降维后,同类点比较散,不集中。解决方案是换成联合概率。
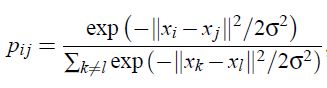

但实践上采用
![]()
Why?
离群点的影响。可如下图所示(涂黑表示很小),假设2号点是离群点,离所有的点都很远,那么左边是未引入对称化的相似度矩阵(矩阵值表示的是相对值,因为有归一化),右侧是采用联合概率的相似矩阵,这个肯定是对称阵,所以可以看到2对任何点的距离都很小了。(均以黑色表示)若采用
![]()
(计算上就是(P+P转置)/2)
则不会有此问题,第离群点距离其他点的相对远近还可以正确表达。

这就是第一点改进,并不是最重要的一点。相比原SNE其效果并未显著提高,原话是 some times even better
2.解决拥挤问题
修改了对降维后数据的相似函数定义。这是全文最精彩的部分。改为t分布

这里形式上于单位柯西分布一致。
修改原理可这样理解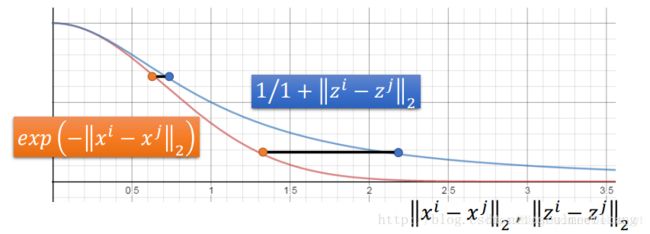
上图画出两个分布的对比,t分布有更长的尾巴。横轴是距离,纵轴表示相似度,越大越相似。直观解释是,在以相似度最接近为优化目标时,算法对于原来就相似的点对(比如属于同类的点对就是这种),不希望降维后分的太开,相对小的距离就很满意了。而对原来不那么相似的(比如不属于同一类的点对),就得距离很大才足够满意。这样的结果是同类拉近,异类排斥,正式所期望的结果。
这个对相似函数精巧设计很有启发性,十分巧妙。
实现
完整代码,jupyter,数据见文末
之前自己实现有些问题,后来参考了原作者给出的numpy实现做了些修改。
具体实现思路是这样的,先算出来降维前的相似度(显然只需计算一次),然后调降维结果来让降维后相似度尽可能逼近之。
第一步,计算降维前点对相似度P
观察p(j|i)公式,发现每个点都有自己的方差,这个如何确定?这个方差大小显著影响点对其附近多远的点考虑临近,显然不能全取1了之,具体方法如下
1.用户设置一个超参数:困惑度(perp),通常取5-50
2.对每个点i,找出σi使得
![]()
其中H为香农熵

为什么这样?香农熵表达的是混乱程度,这里实际意义是点i的邻近点多少,原始数据集里,点在某些地方密度大,某些地方密度小,故为达到相同的困惑度。在密度大的地方的点,σi会小一些,反之大一些。具体计算可通过二分查找确定,因为σi与困惑度是正相关的,通过二分查找很快就可迭代到满意精度(e-5量级)
这样模型通过不同的σi就考虑了数据集在原高纬空间分布不均匀的问题
def cal_distance(self, data):
'''计算欧氏距离
https://stackoverflow.com/questions/37009647/
Arguments:
data {Tensor} -- N*features
Returns:
Tensor -- N*N 距离矩阵,D[i,j]为distance(data[i],data[j])
'''
assert data.dim() == 2, '应为N*features'
r = (data*data).sum(dim=1, keepdim=True)
D = r-2*data@data.t()+r.t()
return D
def Hbeta(self, D, beta=1.0):
'''计算给定某一行(n,)与sigma的pj|i与信息熵H
Arguments:
D {np array} -- 距离矩阵的i行,不包含与自己的,大小(n-1,)
Keyword Arguments:
beta {float} -- 即1/(2sigma^2) (default: {1.0})
Returns:
(H,P) -- 信息熵 , 概率pj|i
'''
# Compute P-row and corresponding perplexity
P = np.exp(-D.copy() * beta)
sumP = sum(P)
H = np.log(sumP) + beta * np.sum(D * P) / sumP
P = P / sumP
return H, P
def p_j_i(self, distance_matrix, tol=1e-5, perplexity=30):
'''由距离矩阵计算p(j|i)矩阵,应用二分查找寻找合适sigma
Arguments:
distance_matrix {np array} -- 距离矩阵(n,n)
Keyword Arguments:
tol {float} -- 二分查找允许误差 (default: {1e-5})
perplexity {int} -- 困惑度 (default: {30})
Returns:
np array -- p(j|i)矩阵
'''
print("Computing pairwise distances...")
(n, d) = self.X.shape
D = distance_matrix
P = np.zeros((n, n))
beta = np.ones((n, 1))
logU = np.log(perplexity)
# 遍历每一个数据点
for i in range(n):
if i % 500 == 0:
print("Computing P-values for point %d of %d..." % (i, n))
# 准备Di,
betamin = -np.inf
betamax = np.inf
Di = D[i, np.concatenate((np.r_[0:i], np.r_[i+1:n]))]
(H, thisP) = self.Hbeta(Di, beta[i])
Hdiff = H - logU
tries = 0
# 开始二分搜索,直到满足误差要求或达到最大尝试次数
while np.abs(Hdiff) > tol and tries < 50:
if Hdiff > 0:
betamin = beta[i].copy()
if betamax == np.inf or betamax == -np.inf:
beta[i] = beta[i] * 2.
else:
beta[i] = (beta[i] + betamax) / 2.
else:
betamax = beta[i].copy()
if betamin == np.inf or betamin == -np.inf:
beta[i] = beta[i] / 2.
else:
beta[i] = (beta[i] + betamin) / 2.
(H, thisP) = self.Hbeta(Di, beta[i])
Hdiff = H - logU
tries += 1
# 最后将算好的值写至P,注意pii处为0
P[i, np.concatenate((np.r_[0:i], np.r_[i+1:n]))] = thisP
print("Mean value of sigma: %f" % np.mean(np.sqrt(1 / beta)))
return P
这里欧拉距离矩阵的计算采用了我采用了向量化实现,详见注释,蛮interesting的。p_j_i的实现主要套用了原作者实现。这里说明下代码里H的计算公式是手动化简了的,很好化简,化简后结果大大提高了计算效率并保证了计算稳定性。
之后可计算出对称的P
def cal_P(self, data):
'''计算对称相似度矩阵
Arguments:
data {Tensor} - - N*N
Keyword Arguments:
sigma {Tensor} - - N个sigma(default: {None})
Returns:
Tensor - - N*N
'''
distance = self.cal_distance(data) # 计算距离矩阵
P = self.p_j_i(distance.numpy(), perplexity=self.perp) # 计算原分布概率矩阵
P = t.from_numpy(P).float() # p_j_i为numpy实现的,这里变回Tensor
P = (P + P.t())/P.sum() # 对称化
P = P * 4. # 夸张
P = t.max(P, t.tensor(1e-12)) # 保证计算稳定性
return P
P = (P + P.t())/P.sum() 这里与论文式子不大一样,多归一化了一些,其实无所谓。夸张是论文提到的小trick,在迭代前几十次时使用,目的是加快优化速度。
第二步
定义降维后点对相似度矩阵Q,这个函数会在迭代中反复调用
def cal_Q(self, data):
'''计算降维后相似度矩阵
Arguments:
data {Tensor} - - Y, N*2
Returns:
Tensor - - N*N
'''
Q = (1.0+self.cal_distance(data))**-1
# 对角线强制为零
Q[t.eye(self.N, self.N, dtype=t.long) == 1] = 0
Q = Q/Q.sum()
Q = t.max(Q, t.tensor(1e-12)) # 保证计算稳定性
return Q
第三步 硬train一发
既然选择pytorch,就没求导数了。直接捏着loss函数train就好了,嗯。
def train(self, epoch=1000, lr=10, weight_decay=0, momentum=0.9, show=False):
'''训练
Keyword Arguments:
epoch {int} -- 迭代次数 (default: {1000})
lr {int} -- 学习率,典型10-100 (default: {10})
weight_decay {int} -- L2正则系数 (default: {0})
momentum {float} -- 动量 (default: {0.9})
show {bool} -- 是否显示训练信息 (default: {False})
Returns:
Tensor -- 降维结果(n,2)
'''
# 先算出原分布的相似矩阵
P = self.cal_P(self.X)
optimizer = optim.SGD(
[self.Y],
lr=lr,
weight_decay=weight_decay,
momentum=momentum
)
loss_his = []
print('training started @lr={},epoch={},weight_decay={},momentum={}'.format(
lr, epoch, weight_decay, momentum))
for i in range(epoch):
if i % 100 == 0:
print('running epoch={}'.format(i))
if epoch == 100:
P = P/4.0 # 100轮后取消夸张
optimizer.zero_grad()
Q = self.cal_Q(self.Y)
loss = (P*t.log(P/Q)).sum()
loss_his.append(loss.item())
loss.backward()
optimizer.step()
print('train complete!')
if show:
print('final loss={}'.format(loss_his[-1]))
plt.plot(np.log10(loss_his))
loss_his = []
plt.show()
return self.Y.detach()
结果
用论文作者给的MNIST子集测试下。喂数据前先吧数据用PCA降到30维

对比下sklearn
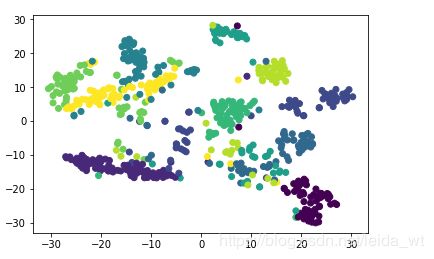
半斤八两吧。有几个数字分的还不错。论文提到要通过随机尝试得到最佳结果。
tSNE的计算复杂度是比较高的,有N^2级别,工业上有NlogN的近似实现。
总结
- 实现时要注意计算稳定性,尤其是0对log和除法的影响,max(data,1e-12)是个很好的实现,同时手动化简下表达式也很有帮助。
- 向量化计算欧拉距离的方法很有启发性
- 论文通过分析修改原方法通过直观感觉定义的函数的做法很有启发性
- 解决离群点的做法很有启发性
参考
Visualizing Data using t-SNE
李宏毅机器学习
下载
链接: https://pan.baidu.com/s/1HQjsXiavCyDNigpl93ITpQ 提取码: wwiv