- Cell Insight | 单细胞测序技术又一新发现,可用于HIV-1和Mtb共感染个体诊断
尐尐呅
结核病是艾滋病合并其他疾病中导致患者死亡的主要原因。其中结核病由结核分枝杆菌(Mycobacteriumtuberculosis,Mtb)感染引起,获得性免疫缺陷综合症(艾滋病)由人免疫缺陷病毒(Humanimmunodeficiencyvirustype1,HIV-1)感染引起。国家感染性疾病临床医学研究中心/深圳市第三人民医院张国良团队携手深圳华大生命科学研究院吴靓团队,共同研究得出单细胞测序
- ArcGIS栅格计算器常见公式(赋值、0和空值的转换、补充栅格空值)
研学随笔
arcgis经验分享
我们在使用ArcGIS时通常经常用到栅格计算器,今天主要给大家介绍我日常中经常用到的几个公式,供大家参考学习。将特定值(-9999)赋值为0,例如-9999.Con("raster"==-9999,0,"raster")2.给空值赋予特定的值(如0)Con(IsNull("raster"),0,"raster")3.将特定的栅格值(如1)赋值为空值,其他保留原值SetNull("raster"==
- 网易严选官方旗舰店,优质商品,卓越服务
高省_飞智666600
网易严选官方旗舰店是网易旗下的一家电商平台,以提供优质商品和卓越服务而闻名。作为一名SEO优化师,我将为您详细介绍网易严选官方旗舰店,并重点强调其特点和优势。大家好!我是高省APP最大团队&联合创始人飞智导师。相较于其他返利app,高省APP的佣金更高,模式更好,最重要的是,终端用户不会流失!高省APP佣金更高,模式更好,终端用户不流失。【高省】是一个自用省钱佣金高,分享推广赚钱多的平台,百度有几
- 探索OpenAI和LangChain的适配器集成:轻松切换模型提供商
nseejrukjhad
langchaineasyui前端python
#探索OpenAI和LangChain的适配器集成:轻松切换模型提供商##引言在人工智能和自然语言处理的世界中,OpenAI的模型提供了强大的能力。然而,随着技术的发展,许多人开始探索其他模型以满足特定需求。LangChain作为一个强大的工具,集成了多种模型提供商,通过提供适配器,简化了不同模型之间的转换。本篇文章将介绍如何使用LangChain的适配器与OpenAI集成,以便轻松切换模型提供商
- 其二
十八尾喵
你知道吗?图片发自App我今天知道了你有喜欢的人,不是我。心空空的,整个人都不是我的了。可,怎么办?还是要好好的活着,毕竟你喜欢的人,我不能杀,可是我可以杀其他喜欢你的人呀!也罢,此生无缘,来世再见。鱼干
- 简介Shell、zsh、bash
zhaosuningsn
Shellzshbashshelllinuxbash
Shell是Linux和Unix的外壳,类似衣服,负责外界与Linux和Unix内核的交互联系。例如接收终端用户及各种应用程序的命令,把接收的命令翻译成内核能理解的语言,传递给内核,并把内核处理接收的命令的结果返回给外界,即Shell是外界和内核沟通的桥梁或大门。Linux和Unix提供了多种Shell,其中有种bash,当然还有其他好多种。Mac电脑中不但有bash,还有一个zsh,预装的,据说
- Python中深拷贝与浅拷贝的区别
yuxiaoyu.
转自:http://blog.csdn.net/u014745194/article/details/70271868定义:在Python中对象的赋值其实就是对象的引用。当创建一个对象,把它赋值给另一个变量的时候,python并没有拷贝这个对象,只是拷贝了这个对象的引用而已。浅拷贝:拷贝了最外围的对象本身,内部的元素都只是拷贝了一个引用而已。也就是,把对象复制一遍,但是该对象中引用的其他对象我不复
- 厉国刚:新闻学与传播学到底有何区别
微观大道
厉国刚:新闻学与传播学到底有何区别头几天,有人在知乎上问我:新闻学与传播学到底有何区别。他是一位想要跨专业考研的学生,对新闻传播学学科可谓了解甚少,甚至一头雾水,想要让我帮他解释解释。在研究生学硕层面,新闻传播学是一级学科,分成新闻学、传播学这两个二级学科。有些高校,还自设了广告学、出版发行学等其他二级学科,但从官方角度,新闻传播学一级学科下,正统的就是那两个二级学科。招生时,一般会按一级学科招,
- 简单了解 JVM
记得开心一点啊
jvm
目录♫什么是JVM♫JVM的运行流程♫JVM运行时数据区♪虚拟机栈♪本地方法栈♪堆♪程序计数器♪方法区/元数据区♫类加载的过程♫双亲委派模型♫垃圾回收机制♫什么是JVMJVM是JavaVirtualMachine的简称,意为Java虚拟机。虚拟机是指通过软件模拟的具有完整硬件功能的、运行在一个完全隔离的环境中的完整计算机系统(如:JVM、VMwave、VirtualBox)。JVM和其他两个虚拟机
- 关于Mysql 中 Row size too large (> 8126) 错误的解决和理解
秋刀prince
mysqlmysql数据库
提示:啰嗦一嘴,数据库的任何操作和验证前,一定要记得先备份!!!不会有错;文章目录问题发现一、问题导致的可能原因1、页大小2、行格式2.1compact格式2.2Redundant格式2.3Dynamic格式2.4Compressed格式3、BLOB和TEXT列二、解决办法1、修改页大小(不推荐)2、修改行格式3、修改数据类型为BLOB和TEXT列4、其他优化方式(可以参考使用)4.1合理设置数据
- 【从浅识到熟知Linux】Linux发展史
Jammingpro
从浅学到熟知Linuxlinux运维服务器
归属专栏:从浅学到熟知Linux个人主页:Jammingpro每日努力一点点,技术变化看得见文章前言:本篇文章记录Linux发展的历史,因在介绍Linux过程中涉及的其他操作系统及人物,本文对相关内容也有所介绍。文章目录Unix发展史Linux发展史开源Linux官网企业应用情况发行版本在学习Linux前,我们可能都会问Linux从哪里来?它是如何发展的。但在介绍Linux之前,需要先介绍一下Un
- 如何培养兴趣
绽蕊向阳
今天读李笑来的书《与时间做朋友》,读到有关兴趣部分,深有感触。书中提到,好多人说对某事没有兴趣,实际上是没有能力把这件事做好,做这件事时的感受很不好,有挫败感,每个人对自己不擅长做不好的事情,都本能的容易逃避,所以就以为自己对这件事不感兴趣,他们真正感兴趣的是其他事情。可事实上,出现这种感觉应该仅仅是因为还没有开始做那件事情,也还没有在那件事情上遭受挫折而已。其实,很多人真的放弃原来做的事情,转去
- 戴容容 中原焦点团队.网络初级第33期,坚持分享第19天 2022年3月9日
TessDai
《每个人眼中的世界都是不同的》“一千个人眼里有一千个哈姆雷特”世界是多元的,每个人都有自己的道理,人人按照自己的理解去看待这个世界的人和物.我们如此,其他人也是如此.因此,任何事情,我们要放下自己以为的真理,去理解他人认为的真理,只有同频方能共振.孩子在慢慢长大的过程中慢慢学会独立,甚至对抗.尤其当孩子处于青春期的时候,他们开始有很多自己独立的想法,和一些特立独行的做法,家长常常会觉得不可思议,觉
- 系统架构设计师 需求分析篇二
AmHardy
软件架构设计师系统架构需求分析面向对象分析分析模型UML和SysML
面向对象分析方法1.用例模型构建用例模型一般需要经历4个阶段:识别参与者:识别与系统交互的所有事物。合并需求获得用例:将需求分配给予其相关的参与者。细化用例描述:详细描述每个用例的功能。调整用例模型:优化用例之间的关系和结构,前三个阶段是必需的。2.用例图的三元素参与者:使用系统的用户或其他外部系统和设备。用例:系统所提供的服务。通信关联:参与者和用例之间的关系,或用例与用例之间的关系。3.识别参
- 每时每刻都是开始2019-03-09
Action熊猫
过去有多少想了无数遍要做的,但实际并没有做到的。以没时间,或其他种种自己认为可以接受的理由,看着一天走啦,一月去啦,又是一年。最后笑一笑,新年不是来了吗!重新开始...如果在过去的365天里,每次醒来,都没能开始,那新年来了,又如何呢?何不把人生的每时每刻都作为起点,不等待,不期盼,不自欺,让每时每刻都在开始中...。
- 2022-02-15
百味人生摆渡人
习惯她和他在谈恋时,就吵架,有时吵的还很厉害,不像其他恋人,恋爱期间有说不完的情话,享受不尽的温情,珍惜在一块的每一分每一秒。分手也分了无数次,不知怎的,就是没有分开。不见面时,特想见面,见了面时,说不了几句,又就开始吵,吵的次数多了,连他们自己也说不清值不值得吵,为什么吵。她妈妈说,这孩子从小就性格倔强。他爸爸说,这孩子从小就性格固执。想想其实也没什么大事。为吃什么吵为穿什么吵为说什么吵……日子
- android 更改窗口的层次,浮窗开发之窗口层级
Ms.Bu
android更改窗口的层次
最近在项目中遇到了这样的需求:需要在特定的其他应用之上悬浮自己的UI交互(拖动、输入等复杂的UI交互),和九游的浮窗类似,不过我们的比九游的体验更好,我们越过了很多授权的限制。浮窗效果很多人都知道如何去实现一个简单的浮窗,但是却很少有人去深入的研究背后的流程机制,由于项目中浮窗交互比较复杂,遇到了些坑查看了很多资料,故总结浮窗涉及到的知识点:窗口层级关系(浮窗是如何“浮”的)?浮窗有哪些限制,如何
- 06选课支付模块之基于消息队列发送支付通知消息
echo 云清
学成在线javarabbitmq消息队列支付通知学成在线
消息队列发送支付通知消息需求分析订单服务作为通用服务,在订单支付成功后需要将支付结果异步通知给其他对接的微服务,微服务收到支付结果根据订单的类型去更新自己的业务数据技术方案使用消息队列进行异步通知需要保证消息的可靠性即生产端将消息成功通知到服务端:消息发送到交换机-->由交换机发送到队列-->消费者监听队列,收到消息进行处理,参考文章02-使用Docker安装RabbitMQ-CSDN博客生产者确
- 基于STM32的汽车仪表显示系统:集成CAN、UART与I2C总线设计流程
极客小张
stm32汽车嵌入式硬件物联网单片机c语言
一、项目概述项目目标与用途本项目旨在设计和实现一个基于STM32微控制器的汽车仪表显示系统。该系统能够实时显示汽车的速度、转速、油量等关键信息,并通过CAN总线与其他汽车控制单元进行通信。这种仪表显示系统不仅提高了驾驶的安全性和便捷性,还能为汽车提供更智能的用户体验。技术栈关键词微控制器:STM32显示技术:TFTLCD/OLED传感器:速度传感器、温度传感器、油量传感器通信协议:CAN总线、UA
- 淘陶居老袁藏品
东海堂
【造像艺术】文化遗产•汉地木造像的区域特征、古代精品造像欣赏。。。。。。(来源:蠢牛/颜旭茂)原创2016-06-12作者:作者:蠢牛(颜旭茂)木造像的地位一直挺尴尬的。国外大型博物馆的木造像基本都是宋元以前的,明代只藏极品。国内也就故宫、国博和上博有能力弄几尊宋木,山西省博貌似只有一尊顶级的明代菩萨能拿得出手,其他木雕大省的博物馆再怎么也应当展示些明清木雕吧,总比同时代那什么坛坛罐罐更有艺术性。
- 【创客文案社】第三期写手招募
筱瑶123
创客文案社第三期写手招募开始了。要求:1:注册一个月以上2:本身热爱写作3:有时间参与接单投稿参与方式:可以关注公众号:写作灵感;也可以通过其他转发文章的文友帮忙拉入群;也可以简信我。参与之后的文友,会先进入新人班,进行基本的试稿与培训,先接一些比较简单的单子;在这里可以一边赚钱,一边学习。不知不觉,来三四个月了,也发现了很多很有意思的现象。1:在上写一篇文章,基本都是几毛钱,多的也不过几块钱的收
- 中国广电永久9元流量套餐!性价比最高流量卡套餐介绍!
优惠攻略官
中国广电是中国最大的传媒集团之一,其推出的流量套餐备受消费者青睐。中国广电最实惠的流量套餐不仅价格亲民,而且提供了优质的网络体验。首先,中国广电的流量套餐价格实惠,适合不同消费者的需求。无论是短期的日租卡还是长期有效的月租卡,用户都可以根据自己的实际情况选择适合自己的套餐。而且,流量的价格相对于其他运营商的套餐来说更加合理,给用户提供了更大的选择空间。☞大流量卡套餐「→点这免费申请办理」或者截图扫
- Python实现TIFF 文件转换为 PNG 和 JPG 格式
sand&wich
python开发语言
在日常的图像处理工作中,可能会遇到需要将TIFF格式的图像转换为其他格式的情况,例如PNG和JPG。下面,本文将介绍如何使用Python和GDAL库实现这一功能。准备工作在开始之前,请确保已经安装了必要的库:GDAL(GeospatialDataAbstractionLibrary)可以使用以下命令安装GDAL:pipinstallgdal代码实现以下是一个将TIFF文件转换为PNG文件的示例代码
- Python 课程10-单元测试
可愛小吉
Python教學python单元测试开发语言TDDunittest
前言在现代软件开发中,单元测试已成为一种必不可少的实践。通过测试,我们可以确保每个功能模块在开发和修改过程中按预期工作,从而减少软件缺陷,提高代码质量。而测试驱动开发(TDD)则进一步将测试作为开发的核心部分,先编写测试,再编写代码,以测试为指导开发出更稳定、更可靠的代码。Python提供了强大的unittest模块,它是Python标准库的一部分,专门用于编写和执行单元测试。与其他测试框架相比,
- 计算机毕业设计PHP仓储综合管理系统(源码+程序+VUE+lw+部署)
java毕设程序源码王哥
php课程设计vue.js
该项目含有源码、文档、程序、数据库、配套开发软件、软件安装教程。欢迎交流项目运行环境配置:phpStudy+Vscode+Mysql5.7+HBuilderX+Navicat11+Vue+Express。项目技术:原生PHP++Vue等等组成,B/S模式+Vscode管理+前后端分离等等。环境需要1.运行环境:最好是小皮phpstudy最新版,我们在这个版本上开发的。其他版本理论上也可以。2.开发
- Python编程 - 初识面向对象
易辰君
Python核心编程python开发语言
目录前言一、面向对象二、类和对象(一)类简介定义类(二)对象简介创建对象(三)总结三、实例属性和实例方法(一)实例属性创建的基本语法使用示例(二)实例方法定义实例方法的基本语法调用示例方法的示例(三)总结四、类中的self(一)基本概念(二)作用访问实例属性调用其他实例方法在构造函数中初始化对象(三)总结五、__init__方法(一)__init__方法的特点(二)基本语法(三)示例(四)总结前言
- [实践应用] 深度学习之模型性能评估指标
YuanDaima2048
深度学习工具使用深度学习人工智能损失函数性能评估pytorchpython机器学习
文章总览:YuanDaiMa2048博客文章总览深度学习之模型性能评估指标分类任务回归任务排序任务聚类任务生成任务其他介绍在机器学习和深度学习领域,评估模型性能是一项至关重要的任务。不同的学习任务需要不同的性能指标来衡量模型的有效性。以下是对一些常见任务及其相应的性能评估指标的详细解释和总结。分类任务分类任务是指模型需要将输入数据分配到预定义的类别或标签中。以下是分类任务中常用的性能指标:准确率(
- [实践应用] 深度学习之优化器
YuanDaima2048
深度学习工具使用pytorch深度学习人工智能机器学习python优化器
文章总览:YuanDaiMa2048博客文章总览深度学习之优化器1.随机梯度下降(SGD)2.动量优化(Momentum)3.自适应梯度(Adagrad)4.自适应矩估计(Adam)5.RMSprop总结其他介绍在深度学习中,优化器用于更新模型的参数,以最小化损失函数。常见的优化函数有很多种,下面是几种主流的优化器及其特点、原理和PyTorch实现:1.随机梯度下降(SGD)原理:随机梯度下降通过
- wandb一直上传 解决方案
行业边缘的摸鱼怪
bug解决方案服务器linux服务器
问题描述运行带有wandb的代码时,虽然可以实现及时同步非常方便,但当设置错参数或其他原因不得不使用ctrl+C停止运行时,总会出现wandb一直上传个不停的现象,给在同一终端重新运行新的代码造成困难。解决方案运行以下代码把wandb的进程直接杀死。psaux|grepwandb|grep-vgrep|awk'{print$2}'|xargskill-9参考链接[CLI]:Ctrl+Ctokill
- Python实现关联规则推荐
这孩子谁懂哈
PythonMachineLearningpython关联规则机器学习
1.什么关联规则关联规则(AssociationRules)是反映一个事物与其他事物之间的相互依存性和关联性,如果两个或多个事物之间存在一定的关联关系,那么,其中一个事物就能通过其他事物预测到。关联规则是数据挖掘的一个重要技术,用于从大量数据中挖掘出有价值的数据项之间的相关关系。关联规则挖掘的最经典的例子就是沃尔玛的啤酒与尿布的故事,通过对超市购物篮数据进行分析,即顾客放入购物篮中不同商品之间的关
- redis学习笔记——不仅仅是存取数据
Everyday都不同
returnSourceexpire/delincr/lpush数据库分区redis
最近项目中用到比较多redis,感觉之前对它一直局限于get/set数据的层面。其实作为一个强大的NoSql数据库产品,如果好好利用它,会带来很多意想不到的效果。(因为我搞java,所以就从jedis的角度来补充一点东西吧。PS:不一定全,只是个人理解,不喜勿喷)
1、关于JedisPool.returnSource(Jedis jeids)
这个方法是从red
- SQL性能优化-持续更新中。。。。。。
atongyeye
oraclesql
1 通过ROWID访问表--索引
你可以采用基于ROWID的访问方式情况,提高访问表的效率, , ROWID包含了表中记录的物理位置信息..ORACLE采用索引(INDEX)实现了数据和存放数据的物理位置(ROWID)之间的联系. 通常索引提供了快速访问ROWID的方法,因此那些基于索引列的查询就可以得到性能上的提高.
2 共享SQL语句--相同的sql放入缓存
3 选择最有效率的表
- [JAVA语言]JAVA虚拟机对底层硬件的操控还不完善
comsci
JAVA虚拟机
如果我们用汇编语言编写一个直接读写CPU寄存器的代码段,然后利用这个代码段去控制被操作系统屏蔽的硬件资源,这对于JVM虚拟机显然是不合法的,对操作系统来讲,这样也是不合法的,但是如果是一个工程项目的确需要这样做,合同已经签了,我们又不能够这样做,怎么办呢? 那么一个精通汇编语言的那种X客,是否在这个时候就会发生某种至关重要的作用呢?
&n
- lvs- real
男人50
LVS
#!/bin/bash
#
# Script to start LVS DR real server.
# description: LVS DR real server
#
#. /etc/rc.d/init.d/functions
VIP=10.10.6.252
host='/bin/hostname'
case "$1" in
sta
- 生成公钥和私钥
oloz
DSA安全加密
package com.msserver.core.util;
import java.security.KeyPair;
import java.security.PrivateKey;
import java.security.PublicKey;
import java.security.SecureRandom;
public class SecurityUtil {
- UIView 中加入的cocos2d,背景透明
374016526
cocos2dglClearColor
要点是首先pixelFormat:kEAGLColorFormatRGBA8,必须有alpha层才能透明。然后view设置为透明glView.opaque = NO;[director setOpenGLView:glView];[self.viewController.view setBackgroundColor:[UIColor clearColor]];[self.viewControll
- mysql常用命令
香水浓
mysql
连接数据库
mysql -u troy -ptroy
备份表
mysqldump -u troy -ptroy mm_database mm_user_tbl > user.sql
恢复表(与恢复数据库命令相同)
mysql -u troy -ptroy mm_database < user.sql
备份数据库
mysqldump -u troy -ptroy
- 我的架构经验系列文章 - 后端架构 - 系统层面
agevs
JavaScriptjquerycsshtml5
系统层面:
高可用性
所谓高可用性也就是通过避免单独故障加上快速故障转移实现一旦某台物理服务器出现故障能实现故障快速恢复。一般来说,可以采用两种方式,如果可以做业务可以做负载均衡则通过负载均衡实现集群,然后针对每一台服务器进行监控,一旦发生故障则从集群中移除;如果业务只能有单点入口那么可以通过实现Standby机加上虚拟IP机制,实现Active机在出现故障之后虚拟IP转移到Standby的快速
- 利用ant进行远程tomcat部署
aijuans
tomcat
在javaEE项目中,需要将工程部署到远程服务器上,如果部署的频率比较高,手动部署的方式就比较麻烦,可以利用Ant工具实现快捷的部署。这篇博文详细介绍了ant配置的步骤(http://www.cnblogs.com/GloriousOnion/archive/2012/12/18/2822817.html),但是在tomcat7以上不适用,需要修改配置,具体如下:
1.配置tomcat的用户角色
- 获取复利总收入
baalwolf
获取
public static void main(String args[]){
int money=200;
int year=1;
double rate=0.1;
&
- eclipse.ini解释
BigBird2012
eclipse
大多数java开发者使用的都是eclipse,今天感兴趣去eclipse官网搜了一下eclipse.ini的配置,供大家参考,我会把关键的部分给大家用中文解释一下。还是推荐有问题不会直接搜谷歌,看官方文档,这样我们会知道问题的真面目是什么,对问题也有一个全面清晰的认识。
Overview
1、Eclipse.ini的作用
Eclipse startup is controlled by th
- AngularJS实现分页功能
bijian1013
JavaScriptAngularJS分页
对于大多数web应用来说显示项目列表是一种很常见的任务。通常情况下,我们的数据会比较多,无法很好地显示在单个页面中。在这种情况下,我们需要把数据以页的方式来展示,同时带有转到上一页和下一页的功能。既然在整个应用中这是一种很常见的需求,那么把这一功能抽象成一个通用的、可复用的分页(Paginator)服务是很有意义的。
&nbs
- [Maven学习笔记三]Maven archetype
bit1129
ArcheType
archetype的英文意思是原型,Maven archetype表示创建Maven模块的模版,比如创建web项目,创建Spring项目等等.
mvn archetype提供了一种命令行交互式创建Maven项目或者模块的方式,
mvn archetype
1.在LearnMaven-ch03目录下,执行命令mvn archetype:gener
- 【Java命令三】jps
bit1129
Java命令
jps很简单,用于显示当前运行的Java进程,也可以连接到远程服务器去查看
[hadoop@hadoop bin]$ jps -help
usage: jps [-help]
jps [-q] [-mlvV] [<hostid>]
Definitions:
<hostid>: <hostname>[:
- ZABBIX2.2 2.4 等各版本之间的兼容性
ronin47
zabbix更新很快,从2009年到现在已经更新多个版本,为了使用更多zabbix的新特性,随之而来的便是升级版本,zabbix版本兼容性是必须优先考虑的一点 客户端AGENT兼容
zabbix1.x到zabbix2.x的所有agent都兼容zabbix server2.4:如果你升级zabbix server,客户端是可以不做任何改变,除非你想使用agent的一些新特性。 Zabbix代理(p
- unity 3d还是cocos2dx哪个适合游戏?
brotherlamp
unity自学unity教程unity视频unity资料unity
unity 3d还是cocos2dx哪个适合游戏?
问:unity 3d还是cocos2dx哪个适合游戏?
答:首先目前来看unity视频教程因为是3d引擎,目前对2d支持并不完善,unity 3d 目前做2d普遍两种思路,一种是正交相机,3d画面2d视角,另一种是通过一些插件,动态创建mesh来绘制图形单元目前用的较多的是2d toolkit,ex2d,smooth moves,sm2,
- 百度笔试题:一个已经排序好的很大的数组,现在给它划分成m段,每段长度不定,段长最长为k,然后段内打乱顺序,请设计一个算法对其进行重新排序
bylijinnan
java算法面试百度招聘
import java.util.Arrays;
/**
* 最早是在陈利人老师的微博看到这道题:
* #面试题#An array with n elements which is K most sorted,就是每个element的初始位置和它最终的排序后的位置的距离不超过常数K
* 设计一个排序算法。It should be faster than O(n*lgn)。
- 获取checkbox复选框的值
chiangfai
checkbox
<title>CheckBox</title>
<script type = "text/javascript">
doGetVal: function doGetVal()
{
//var fruitName = document.getElementById("apple").value;//根据
- MySQLdb用户指南
chenchao051
mysqldb
原网页被墙,放这里备用。 MySQLdb User's Guide
Contents
Introduction
Installation
_mysql
MySQL C API translation
MySQL C API function mapping
Some _mysql examples
MySQLdb
- HIVE 窗口及分析函数
daizj
hive窗口函数分析函数
窗口函数应用场景:
(1)用于分区排序
(2)动态Group By
(3)Top N
(4)累计计算
(5)层次查询
一、分析函数
用于等级、百分点、n分片等。
函数 说明
RANK() &nbs
- PHP ZipArchive 实现压缩解压Zip文件
dcj3sjt126com
PHPzip
PHP ZipArchive 是PHP自带的扩展类,可以轻松实现ZIP文件的压缩和解压,使用前首先要确保PHP ZIP 扩展已经开启,具体开启方法就不说了,不同的平台开启PHP扩增的方法网上都有,如有疑问欢迎交流。这里整理一下常用的示例供参考。
一、解压缩zip文件 01 02 03 04 05 06 07 08 09 10 11
- 精彩英语贺词
dcj3sjt126com
英语
I'm always here
我会一直在这里支持你
&nb
- 基于Java注解的Spring的IoC功能
e200702084
javaspringbeanIOCOffice
- java模拟post请求
geeksun
java
一般API接收客户端(比如网页、APP或其他应用服务)的请求,但在测试时需要模拟来自外界的请求,经探索,使用HttpComponentshttpClient可模拟Post提交请求。 此处用HttpComponents的httpclient来完成使命。
import org.apache.http.HttpEntity ;
import org.apache.http.HttpRespon
- Swift语法之 ---- ?和!区别
hongtoushizi
?swift!
转载自: http://blog.sina.com.cn/s/blog_71715bf80102ux3v.html
Swift语言使用var定义变量,但和别的语言不同,Swift里不会自动给变量赋初始值,也就是说变量不会有默认值,所以要求使用变量之前必须要对其初始化。如果在使用变量之前不进行初始化就会报错:
var stringValue : String
//
- centos7安装jdk1.7
jisonami
jdkcentos
安装JDK1.7
步骤1、解压tar包在当前目录
[root@localhost usr]#tar -xzvf jdk-7u75-linux-x64.tar.gz
步骤2:配置环境变量
在etc/profile文件下添加
export JAVA_HOME=/usr/java/jdk1.7.0_75
export CLASSPATH=/usr/java/jdk1.7.0_75/lib
- 数据源架构模式之数据映射器
home198979
PHP架构数据映射器datamapper
前面分别介绍了数据源架构模式之表数据入口、数据源架构模式之行和数据入口数据源架构模式之活动记录,相较于这三种数据源架构模式,数据映射器显得更加“高大上”。
一、概念
数据映射器(Data Mapper):在保持对象和数据库(以及映射器本身)彼此独立的情况下,在二者之间移动数据的一个映射器层。概念永远都是抽象的,简单的说,数据映射器就是一个负责将数据映射到对象的类数据。
&nb
- 在Python中使用MYSQL
pda158
mysqlpython
缘由 近期在折腾一个小东西须要抓取网上的页面。然后进行解析。将结果放到
数据库中。 了解到
Python在这方面有优势,便选用之。 由于我有台
server上面安装有
mysql,自然使用之。在进行数据库的这个操作过程中遇到了不少问题,这里
记录一下,大家共勉。
python中mysql的调用
百度之后能够通过MySQLdb进行数据库操作。
- 单例模式
hxl1988_0311
java单例设计模式单件
package com.sosop.designpattern.singleton;
/*
* 单件模式:保证一个类必须只有一个实例,并提供全局的访问点
*
* 所以单例模式必须有私有的构造器,没有私有构造器根本不用谈单件
*
* 必须考虑到并发情况下创建了多个实例对象
* */
/**
* 虽然有锁,但是只在第一次创建对象的时候加锁,并发时不会存在效率
- 27种迹象显示你应该辞掉程序员的工作
vipshichg
工作
1、你仍然在等待老板在2010年答应的要提拔你的暗示。 2、你的上级近10年没有开发过任何代码。 3、老板假装懂你说的这些技术,但实际上他完全不知道你在说什么。 4、你干完的项目6个月后才部署到现场服务器上。 5、时不时的,老板在检查你刚刚完成的工作时,要求按新想法重新开发。 6、而最终这个软件只有12个用户。 7、时间全浪费在办公室政治中,而不是用在开发好的软件上。 8、部署前5分钟才开始测试。
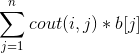 ,这里可以用拓扑排序求出来。最后在乘上a[ i ]就可以了。先建个反向图,然后从入度为0的点开始,求在该点的后继节点+=ans[当前节点] + b[当前节点].
,这里可以用拓扑排序求出来。最后在乘上a[ i ]就可以了。先建个反向图,然后从入度为0的点开始,求在该点的后继节点+=ans[当前节点] + b[当前节点].