【NISP: Pruning Networks using Neuron Importance Score Propagation】论文笔记
简介和综述
论文链接:https://arxiv.org/pdf/1711.05908.pdf
这篇论文对于裁剪部分写的很详细,同时综述也不错。这篇博客只是将论文翻译了一下(大部分机翻)。
为了减少深度卷积神经网络(CNN)中的显着冗余,大多数现有方法仅通过考虑单个层或两个连续层的统计来修剪神经元(例如,修剪一个层以最小化下一层的重建误差),忽略深度网络中误差传播的影响。
相反,我们认为必须根据统一的目标联合修剪整个神经元网络中的神经元:最小化“最终响应层”(FRL)中重要响应的重建误差,这是之前的倒数第二层分类,用于修剪网络以重新训练其预测能力。
具体来说,我们应用特征排序技术来测量每个神经元在FRL中的重要性,并将网络修剪公式化为二元整数优化问题,并为其修剪早期层中神经元的封闭形式解决方案。
基于我们的理论分析,我们提出神经元重要性分数传播(NISP)算法,以传播最终响应对网络中每个神经元的重要性分数。
通过去除最不重要的神经元来修剪CNN,然后进行微调以保持其预测能力。
NISP在具有多个CNN模型的几个数据集上进行评估,并证明可以实现显着的加速和压缩,而精度损失可忽略不计
我们测量神经元在最终响应层(FRL)中的重要性,并推导出神经元重要性分数传播(NISP)以将重要性传播到整个网络。
给定每层预定义的修剪比率,我们修剪具有较低重要性得分的神经元/过滤器。我们最终微调修剪后的模型以恢复其预测准确性。
CNN在训练和测试阶段都需要大量参数和高计算成本。
最近的研究已经研究了深层网络中的显着冗余[6]并且通过修剪不重要的网络来减少神经元和过滤器的数量[3,14,25,29]。
然而,修剪神经元和过滤器的大多数当前方法仅考虑一层的统计数据(例如,具有小幅度重量的剪枝神经元[25,14])或两个连续层[29]来确定神经元的“重要性”。 。
这些方法可以独立[14]或贪婪地[25,29]逐层修剪“最不重要”的神经元,而不考虑不同层中的所有神经元。
这种方法的一个问题是在早期层中被认为不重要的神经元实际上可以显着地促成后面层中重要神经元的响应。
我们的实验(见第4.4节)揭示了贪婪的逐层修剪导致显着的重建误差传播,特别是在深度网络中,这表明需要对CNN的不同层的神经元重要性进行全局测量。
为了解决这个问题,我们认为修剪模型必须在分类之前保留倒数第二层最重要的响应(“最终响应层”(FRL))以重新训练其预测能力,因为这些响应是分类任务的直接输入(也通过特征选择方法提出,例如,[34])。
我们基于统一的目标定义早期层中神经元的重要性:最小化FRL中产生的响应的重建误差。
我们首先通过将它们视为特征并应用一些特征排序技术(例如,[34])来测量FRL中响应的重要性,然后将神经元的重要性从FRL向后传播到早期层。
我们仅修剪具有低传播重要性的节点(即,其移除不会导致大的传播错误的节点)。
从理论的角度来看,我们将网络修剪问题制定为二进制整数规划目标,最小化原始最终响应与修剪网络产生的加权l1距离(与重要性分数成比例)。
我们获得了该目标的宽松版本的封闭形式解决方案,以推断出网络中每个神经元的重要性得分。
基于该解决方案,我们推导出神经元重要性得分传播(NISP)算法,该算法递归地计算所有重要性得分,仅使用最终响应层的一个特征等级和一个向后传递通过网络,如图1所示。

然后基于推断的神经元重要性分数对网络进行修剪并进行微调以保持其预测能力。
我们将每层的修剪比率视为预定义的超参数,其可以基于特定应用的不同需求(例如,FLOP,存储器和精度约束)来确定。
修剪算法是通用的,因为特征排名可以应用于任何感兴趣的层,并且仍然可以传播重要性分数。
此外,NISP不是特定于硬件的。给定预训练模型,NISP输出相同类型的较小网络,可以部署在为原始模型设计的硬件设备上。
我们使用多种标准CNN架构评估我们对MNIST [23],CIFAR10 [21]和ImageNet [5]的方法,如LeNet [23],AlexNet [22],GoogLeNet [37]和ResNet [16]。
我们的实验表明,通过我们的方法修剪的CNN优于那些具有相同结构但是从头开始训练或随机修剪的CNN。
我们证明我们的方法优于基于幅度和逐层修剪。
FLOP的理论减少和不同方法的参数数量的比较表明,我们的方法实现了更快的全网加速和压缩,具有更低的精度损失,例如,我们的方法在Alexnet上损失了1.43%并且在Figurnov时将FLOP降低了67.85%。等。 [11]损失更多(2%)并减少FLOPs(50%)。
由于ResNet-56的精度损失几乎为零,我们实现了FLOP降低43.61%,显着高于Li等人的27.60%降低。 [25]。
我们引入了通用网络修剪算法,该算法将修剪问题表示为二进制整数优化,并基于最终响应重要性提供封闭形式的解决方案。
我们提出NISP有效地传播从最终响应到所有其他神经元的重要性分数。
实验表明,NISP导致CNN中所有类型的层的全网加速和压缩,精度损失很小。
最近有兴趣减少深CNN的冗余以实现加速和压缩。
在[6]中,深度学习模型参数化的冗余已经被研究和证明。
程等人。 [2]利用结构矩阵的特性和使用循环矩阵来表示FC层,降低了存储成本。
韩等人。 [14]通过组合修剪,量化和霍夫曼编码来研究重量稀疏性和压缩的CNN。
在[26,38,36]中,稀疏正则化项用于学习稀疏的CNN结构。
苗等人。 [30]研究了基于浮点数据量化的网络压缩,以实现大规模模型存储。
为了加速卷积层的推理,Jaderberg等人。 [18]通过利用跨通道或滤波器冗余构建了空间域中排名为1的滤波器的低秩基础。
刘等人。 [28]在培训过程中强加了一个比例因子,并促进了一个渠道级别的修剪。
Figurnov等。 [11]通过跳过某些空间位置的操作来加速卷积层,这是基于源代码优化的循环穿孔。
在[7,47,20]中,利用低秩近似方法通过将权重矩阵分解为低秩矩阵来加速卷积层。 Molchanov等。 [31]修剪CNN基于泰勒扩张。
Srinivas等人专注于压缩完全连接的(FC)层。 [35]修剪过的神经元彼此相似。
杨等人。 [43]应用“快餐”变换来重新参数化FC层的矩阵向量乘法。
Ciresan等人。 [3]通过随机修剪神经元来减少参数。
陈等人。 [1]使用低成本散列函数将连接权重随机分组到散列桶中,然后使用反向传播对网络进行微调。
其他研究侧重于定点计算,而不是利用CNN冗余[4,32]。
另一项工作研究了知识蒸馏的基本思想[17]。
吴等人。 [39]建议跳过层以加快推理。
除了上述关注网络压缩的工作外,其他方法还通过改进某些任务的管道来加速深度网络推理[33,13,46,27]。
我们的方法修剪了预先训练好的网络,需要快速收敛的微调过程,而不是从头开始重新训练网络。
为了测量CNN中神经元的重要性,考虑到非线性的复杂性,很难获得精确解。
以前的一些作品[8,9,10]使用二阶泰勒展开来逼近它。
我们的工作是基于神经网络的利普希茨连续条件(Lipschitz continuity)的不同近似。
最类似于我们的方法,Li等人。 [25]按重量大小修剪过滤器。
罗等人。 [29]利用从下一层计算的统计信息来指导贪婪的逐层修剪。
相比之下,我们不仅基于神经元的个体重量而且基于输入数据和网络中的其他神经元的属性来测量神经元重要性。
同时,假设一层只能影响其下一层(可能导致错误传播),而不是以贪婪的方式逐层修剪,我们通过传播最终响应层的重要性来衡量整个网络的重要性。
NISP的概述如图1所示。
给定训练有素的CNN,我们首先在该最终响应层上应用特征排序算法并获得每个神经元的重要性分数。
然后,所提出的NISP算法在整个网络中传播重要性分数。
最后,基于神经元的重要性分数对网络进行修剪并进行微调以恢复其准确性。
最终响应层上的特征排名
我们的直觉是神经网络的最终响应应该在完全网络修剪中发挥关键作用,因为它们是分类任务的直接输入。
因此,在第一步中,我们对最终响应应用特征排名。
值得注意的是,我们的方法可以用于任何对关于特征进行评分的特征选择。 他们的分类能力。
我们采用最近推出的过滤方法Inf-FS [34],因为它在CNN特征选择上的效率和有效性。
Inf-FS利用矩阵幂级数的性质来有效地计算特征相对于所有其他特征的重要性,即,它能够在特征图1中的所有路径上集成特征的重要性。
NISP
我们的目标是在给定最终响应的重要性分数的情况下决定删除哪些中间神经元,以便最大程度地保留网络的预测能力。
我们将此问题表示为二进制整数编程(优化)并提供封闭形式的近似解。
基于我们的理论分析,我们开发了神经元重要性分数传播算法,以有效地计算整个网络的神经元重要性。
问题定义
修剪的目标是去除神经元,同时最小化准确度损失。
由于模型精确度取决于最终响应,我们将目标定义为最小化原始最终响应与神经元被修剪特定层后的最终响应之间的加权距离。
在下文中,我们使用粗体符号来表示向量和矩阵。
大多数神经网络可以表示为嵌套函数。
因此,我们将深度为n的网络定义为函数
 。
。
第l层f(l)使用以下一般形式表示,


具有分支连接的网络(例如ResNet中的跳过连接)可以通过填充权重和合并层转换为该表示。
我们将神经元重要性得分定义为一个关于神经元的非负值,并使用sl来表示第l层中神经元重要性分数的向量。假设Nl神经元在修剪后仍保留在第l层;我们将第l层的神经元修剪标志定义为一个二值向量sl*,然后基于神经元重要性得分sl计算sl的值。当sl,i位于sl中的峰值区间内,使sl,i = 1。
(简言之:对于第l层所有的神经元,如果某个神经元对应的重要性分数位于该层的前列,即保留该神经元,否则裁剪掉。)
Nl → 第l层裁剪后需要保留的神经元
sl → 第l层中神经元重要性分数向量
sl* → 第l层的神经元修剪标志向量(二值向量)
目标函数
我们的目标的动机是,对于重要神经元,原始网络产生的响应与修剪后网络产生的响应之间的差异应该最小化。
使F(n)为具有n层的神经网络。 假设我们有一个M个样本的数据集,每个样本都用x0m表示。
对于第m个样本,我们使用xlm来表示第l层网络的响应。
网络的最终输出将是xnm,其相应的非负神经元重要性是sn。 我们定义G(i,j)作为从第i层到第j层的F(n)的子网络。
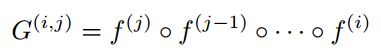
我们的目标是为第l层计算神经元修剪标志向量sl*,以便最小化修剪第l层产生的对最终响应中的重要神经元的影响。
为此,我们定义了一个优化目标,关于第l层神经元修剪指标,对于整个数据集中的所有样本而言:

对于单个样本而言,目标函数定义为:
解决方案
网络修剪问题可以表示为二进制整数问题,在目标函数中找到最佳神经元修剪标志向量。 然而,通过直接优化方程很难获得有效的分析解决方案。 因此,我们得出该目标的上界,并表明通过最小化上界可以获得次优解。 有趣的是,基于这种次优解,我们找到了一种可行且有效的对于所有神经元重要性评分的公式。
回想一下,第k层fk(x)被定义为
![]()
我们假设激活函数σ(k)是利普希茨连续的,因为它通常适用于神经网络中的大多数常用激活函数,例如Identity,ReLU,sigmoid,tanh,PReLU等。然后根据利普希茨连续定理,我们知道对于任意x,y,存在常数Cσ(k),使得
![]()
然后很容易得到:

对于G(i,j)而言:
![]()
则:

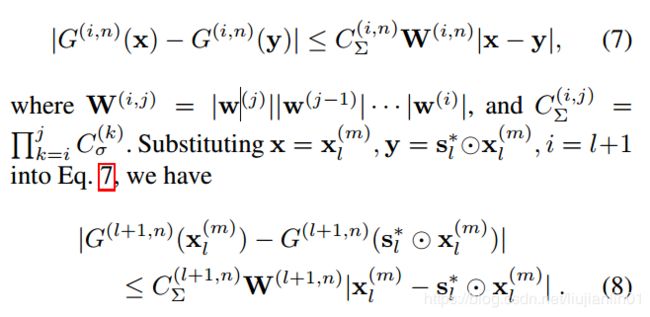
因为sn是一个非负向量,
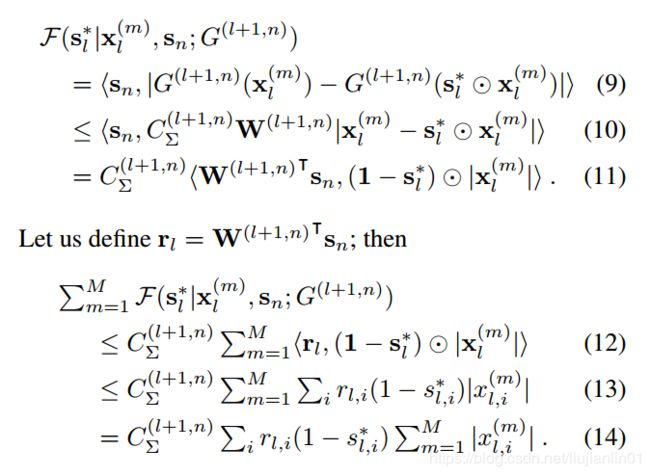

该结论可以应用于网络中的每个层。
基于此结果,我们如下定义网络的神经元重要性。
定义1(神经元重要性评分)。
给定包含n个层的神经网络F(n)和最后一层响应的重要性得分s(n),第k层响应的重要性得分可以计算为

神经元重要性的一个重要特性是它可以沿网络递归(或传播)计算
定义2(神经元重要性得分传播)。
第k层响应的重要性得分可以从第(k + 1)层的重要性得分传播

算法
最初,我们在网络的最终响应层中具有每个神经元的重要性分数。
定义1表明网络中每个其他层的重要性得分与最终响应的重要性直接相关。
然而,我们不是使用定义1来昂贵地计算重要性。 从定义2可以看出,下层的重要性得分可以直接从其上方的相邻层传播。
上式可以等价为:

其中sk,j是第k层响应中第j个神经元的重要性得分。
我们从上式中得出结论:神经元的重要性是与其直接相连的所有后续神经元的加权和。
该结论还适用于网络中的归一化,池化和分支连接(即,一层直接与多个层连接)。
NISP算法从FRL中的重要性开始并重复传播,以通过单个后向传递获得网络中所有神经元的重要性。
裁剪
给定每层的目标修剪比例,我们传播重要性分数,根据其重要性得分计算神经元的修剪指标,并去除修剪指标值为0的神经元。重要性传播和层修剪在一个后向传播中共同发生,并且被修剪的神经元的重要性不会传播到下一层。
对于完全连接的层,我们修剪每个单独的神经元。
对于卷积层,我们将整个神经元通道一起修剪。
计算通道的重要性得分为该通道内所有神经元的重要性得分的总和。
实验
我们使用流行的CNN网络评估我们对标准数据集的方法。
我们首先比较随机修剪和从头开始训练基线,以证明我们方法的有效性。
然后,我们比较两个其他基线,基于幅度的修剪和逐层修剪,分别突出特征排名和神经元重要性得分传播的贡献。
最后,我们对修剪结果进行基准测试,并与现有方法进行比较,如[11,20,36,25]。
Comparison with Random Pruning and Trainfrom-scratch Baselines
我们比较两个基线:(1)随机修剪预训练的CNN,然后进行微调,(2)从头开始训练每层具有相同数量神经元/滤波器的小型CNN作为我们的修剪模型。 除初始学习率外,我们对方法和基线使用相同的实验设置。 对于从头开始的训练,我们将初始学习率设置为原始学习率,而对于微调任务(NISP和随机修剪),初始学习率降低了10倍。
**LeNet on MNIST:**我们修剪了FC层中的一半神经元和图3(a)中两个卷积层中的一半滤波器。
我们的方法表示为NISPHalf,而随机修剪或从头开始训练的基线方法表示为RandomHalf和ScratchHalf。
我们的方法在三个方面优于基线。
首先,对于微调(修剪后),与基线不同,我们的方法在迭代0时具有非常小的精度损失; 这意味着它保留了最重要的神经元,仅修剪冗余或较少辨别的神经元。
其次,我们的方法收敛速度比基线快得多。
第三,我们的方法在微调后具有最小的精度损失。
对于MNIST上的LeNet,与预修剪网络相比,我们的方法仅降低0.02%的前1精度,修剪率为50%。

**Cifar-net on CIFAR10:**学习曲线如图3(b)所示。
类似于在MNIST上进行LeNet实验的观察结果,我们的方法在相同的三个方面优于基线:最低的初始精度损失,最高的收敛速度和微调后的最低精度损失。 我们的方法具有不到1%的前1精度损失,每层50%的修剪比。
**AlexNet on ImageNet:**为了证明我们的方法适用于大而深的CNN,我们在AlexNet上复制实验,所有卷积层和FC层的修剪率为50%(当我们修剪转换层和FC层时表示为NISPCF)。
考虑到AlexNet中FC层的重要性,我们比较了另一种情况,其中我们的方法只修剪了一半的滤波器,但没有修剪FC层中的神经元(表示为NISPC)。
我们将初始学习率降低10倍,然后微调90个时期并报告前5个准确度损失。
图3(c)显示,对于这两种情况(修剪卷积和FC层以及仅修剪卷积层),我们在MNIST和CIFAR10上观察到的优势仍然存在。
可以在补充材料中找到显示全网加速的分层计算简化分析
GoogLeNet on ImageNet: 我们将初始模块中的缩减层表示为“缩小”,将1×1卷积层表示为“1×1”。
我们在训练中使用Caffe的快速解算器。
我们在3种修剪策略的方法和基线之间进行实验:
(Half)将所有卷积层修剪一半;
(noReduce)修剪每个卷积层,除了初始模块中的缩减层减半;
(no1x1)除了初始模块中的1×1层之外,将每个卷积层修剪一半。
我们在图3(d)中显示了其中两个的结果,并观察了与其他CNN网络上的实验类似的模式。
对于所有GoogLeNet实验,我们训练/微调60个时期并报告前5个准确度损失。
Feature Selection v.s. Magnitude of Weights
如何定义神经元的重要性是一个悬而未决的问题。
除了使用特征排序来测量神经元的重要性之外,其他方法[25,29,14]通过权重的大小来测量神经元的重要性。
为了研究不同标准确定神经元重要性时的影响,我们通过固定NISP的其他部分进行实验,并且仅将修剪结果与不同的重要性测量值进行比较:
1.使用[34]中的特征选择方法(NISPFS)
2.仅考虑重量大小(NISPMag)
对于基于幅度的修剪,神经元在最终响应层中的重要性等于连接神经元与其先前层的所有权重的绝对和。
为了仅比较重要性中的两个度量,我们基于其权重值的大小对最终响应层中的神经元的重要性进行排序,并将它们的重要性传播到较低层。最后,我们以与NISP方法相同的方式修剪和微调模型。
对于“NISP-Mag”基线,我们使用AlexNet和Cifar-net架构。这些基线的学习曲线如图4所示。
我们观察到“NISP-FS”在修剪比例与“NISP-Mag”相同的情况下产生的精度损失要小得多,但“NISP-Mag”仍然优于随机修剪和从头开始训练基线,这表明了NISP的有效性。 在本文的其余部分,我们采用了NISP中[34]中提出的特征排序方法。
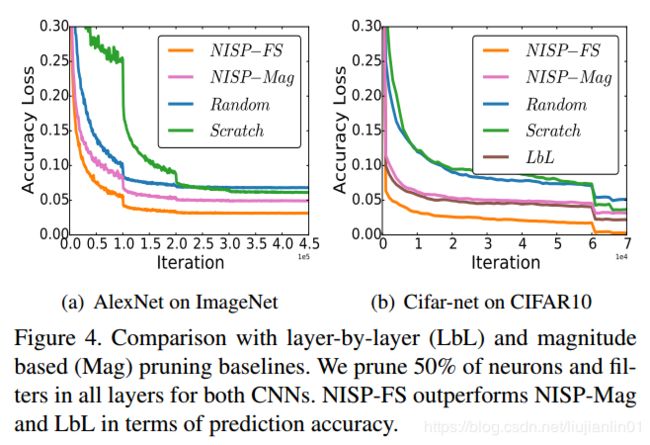
NISP v.s. Layer-by-Layer Pruning
为了证明NISP重要性传播的优势,我们比较了一种修剪方法,该方法在每一层上进行特征排序,以测量神经元的重要性,并独立地修剪每层的不重要神经元。
所有其他设置与NISP相同。
我们称这种方法为“逐层”(LbL)修剪。
“LbL”基线的一个挑战是测量每层上神经元重要性的计算成本是巨大的。 因此,我们选择在CIFAR10数据集上训练的小型CNN结构。 图4(b)显示尽管“LbL”方法优于基线,但在具有相同修剪比的最终精度损失方面,它的表现比NISP差得多,这表明需要使用NISP测量整个网络中神经元的重要性。
为了进一步研究NISP优于逐层修剪的优势,我们定义加权平均重建误差(WARE)来测量修剪后的最终响应层上重要神经元响应的变化(无需微调):

我们设计了不同数量的Conv层的不同Cifar-net-CNNs,并应用不同修剪比例的NISP和LbL修剪。
我们报告了图5中最终响应层(Cifar-net-CNNs中的“ip1”层)中保留神经元的WARE。
我们观察到:
1.随着网络深度的增加,LbL-pruned网络的WARE显着增加,这表明逐层修剪的错误传播问题,特别是当网络很深时,并且表明需要全局修剪方法,如NISP;
2.当修剪比较大时,LbL方法的WARE变得更大,但是当使用NISP修剪网络时更稳定;
3.与LbL相比,NISP方法总是减少保留神经元上的WARE。
NISP获得的最终响应层中重要神经元的小重建误差为微调提供了更好的初始化,这导致修剪网络的精度损失低得多。

*Supplementary Material(细节部分)
我们提出NISP有效地将最终响应的重要性分数传播到所有其他神经元,以指导网络修剪以实现深度网络的加速和压缩。
在补充材料中,我们展示了如何从最终响应层传播神经元重要性的细节,以及一些其他实验。
鉴于神经元的重要性,我们首先确定前一层中用作其输入的位置,然后将重要性传播到与权重成比例的位置。
我们只将所选特征提取器的重要性传播到先前的层,并忽略已修剪的特征提取器。
NISP过程可分为三类:
从1-way张量到1-way张量,例如, FC层之间;
从1-way张量到3-way向张量,例如,从FC层到卷积/池化层;
从3-way张量到3-way张量,例如从池化层到卷积层。
我们通过忽略偏差的传播来简化NISP。
NISP: from 1-way tensor to 1-way tensor
给定具有M个输入神经元和N个输出神经元的FC层,输出特征的重要分数向量Sout(N×1)。
我们使用WFC(M×N)来表示FC层的权重。
输入神经元的重要分数向量是:
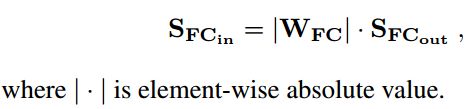
NISP: from 1-way tensor to 3-way tensor
给定具有3-way张量作为输入和N个输出神经元的FC层,输入具有X×X×C的大小,其中X是空间大小,C是输入通道的数量。
输入可以是卷积层或池化层的响应。
我们使用WFC(X×X×C×N) 来表示FC层的权重。 输入张量的重要分数向量Sin(X×X×C×1)是(Sout(N×1)):

NISP: from 3-way tensor to 3-way tensor
Convolution Layer
我们推导出卷积层的NISP,这是3-way张量之间NISP最复杂的情况。
用于池化和本地响应归一化化(LRN)的NISP可以类似地导出。
对于输入3-way张量为CONVin(X×X×N),输出张量为CONVout(Y×Y×F)的卷积层,滤波器大小为k,stride为s,填充像素数为p。
对于输入通道n和输出通道f,对应卷积核kfn。
对于输入张量的第n个通道中的位置i,位置i处的输出通道f的相应响应被定义为:

其中in(i)是卷积核对应的2-D感受野。
给定输出响应的重要性分数向量Sout(Y×Y×F),我们使用类似的线性计算来传播从输出响应到输入的重要性:

其中Sn(i)是位置i在第n个输入通道中的重要性,而Sout(i)是对应的2-D矩阵,其包含其响应来自前向传播期间该输入位置的值的输出位置。
我们按比例传播重要性,如算法1中所述

算法1中使用的传播矩阵:


上面等式意味着卷积层中3-way张量之间的重要性传播可以分解为二维矩阵之间的传播。
对于输入通道n和输出通道f,输入层尺寸为X×X,输出尺寸为Y×Y。
给定输出层的重要性向量Sout,f(1×Y×Y),传播矩阵BPfn,conv((Y×Y)×(X×X)用于映射从Sout,f到输入Sin,fn(1×X×X)的重要性。
BPfn,conv(i, j)不等于0,意味着输出层中的第i个位置来自输入层中第j个位置的卷积运算,我们在两个位置之间传播重要性。我们使用一个Y×X矩阵bi,fn来表示输出层行与其对应的输入层行之间的映射。
在bi,fn的每一行中,存在k个非零,因为输出层中的每个位置是从输入层中一个宽度为k的区域获得的。
bi,fn的每一行的非零值都是卷积核kfn中的第i行。在每行中,权重与开始之间的偏移量是步幅s。
整个传播矩阵BPfn,conv是一个块矩阵,其中每个子矩阵是bi,fn(Y×X)或零矩阵。
BPfn,conv的每一行都有b1,fn到bk,fn,因为卷积核的高度是k。
BPfn,conv的每一行中bs开头的偏移量是步幅s。
例子:X = 4; Y = 2; k = 3; s = 1,如图7所示。

Pooling Layer
假设具有输入大小为X×X×F且输出大小为Y×Y×F的池化层。池化过滤器大小为k,步幅为s。
大多数池化技术的基本思想是相同的:使用固定的2-D滤波器独立地简化每个通道内的局部响应。
例如,在最大池化中,每个输出响应由来自输入响应k×k区域内数值中的最大值组成。
由于输入数据的方差很大,因此可以假设感受野中的最大值服从均匀分布。
因此,对于一个输出响应位置而言,来自输入响应k×k区域内各值的贡献是均等的。
由于池化是一种不跨越通道的空间操作,每个通道的重要性都可以相对独立进行传播。
给定通道f的输出3-way重要性张量Sout,f(1×Y×Y),输入张量的重要性向量计算如下:

考虑一个输入大小为X×X且输出大小为Y×Y的通道。
给定输出层的重要性向量Sout,f(1×Y×Y),传播矩阵BPpooling(Y×Y)×(X×X)用于映射从Sout,f到输入层Sin,f(X×X)的重要性。
如果BPpooling(i,j)=1,则输出层中的第i个位置来自池操作和输入层中的第j个位置,因此我们传播这两个位置之间的重要性。
我们使用一个Y×X矩阵bp来表示输出层中的行与输入层中的对应行之间的映射。
在bp的每一行中,存在k个1,因为输出层中的每个元素是从输入层中具有宽度k的区域中池化的(和卷积一样)。
每个1的偏移量是步幅s。
整个传播矩阵BPpooling是一个块矩阵,子矩阵是大小为Y×X的bp矩阵或零矩阵。
每行BPpooling都有k个bp,因为池化过滤器的高度为k。
这k个bp的偏移量也是步幅s。
每个bp将通过池化过滤器所覆盖位置的数量来进行归一化(与下面所示的LRN层相同)。其他元素都是零。
例子:X = 4, Y = 2, k = 2, s = 2,如图8所示。

Local Response Normalization Layer
Krizhevsky等人。 [22]提出了局部响应归一化(LRN)来改善CNN的泛化性。
对于跨通道LRN,对在相同空间位置处的相邻核映射进行求和产生在该位置处的归一化激活响应。
由于LRN是非线性操作,因此在输入和输出张量之间进行精确的重要性传播是难以处理的。
一种近似传播的方法是假设在考虑输入数据具有大方差时,在某个空间位置处的核映射贡献等于输出张量在该位置处的响应。
然后,给定一个具有local size = l的LRN层响应的重要性张量(X×X×N),l是某个空间位置卷积映射数量的求和。
考虑空间位置(i,j)的所有的N个通道,该空间位置的重要向量是Sout,ij(1×N)。 对应的输入相应重要性向量Sin,ij(1×N)是

对于跨通道LRN,输出响应张量具有与输入相同的形状。
对于输出张量的空间位置(i,j),给定其重要性矢量Sout,ij,我们构造N×N对称矩阵(关于主对角线对称)BPLRN,以将其重要性传播到该位置处的对应输入矢量Sin,ij。
由于LRN操作的中心位于位置(i,j),其操作将覆盖左侧和右侧的(l + 1)/2个位置。
当将矢量Sout,ij作为中心位置(从列(l + 1)/2到N - (l + 1)/2 + 1)进行操作时,其操作覆盖了l个跨通道位置,因此BPLRN中的对应列应有l个1。
当在向量的边缘处进行LRN操作时,由于缺少跨通道位置,使得从列(l + 1)/2到列1(类似于右下角),BPLRN的相应列中1的数目随着从中心到边缘的步数减少(1步少1个1,看图比较容易理解)。
对于通道内LRN,遵循我们的均等分布假设,重要性传播可以与池化层相同。
例子:跨通道,l = 3,N = 5。

PCA Accumulated Energy Analysis
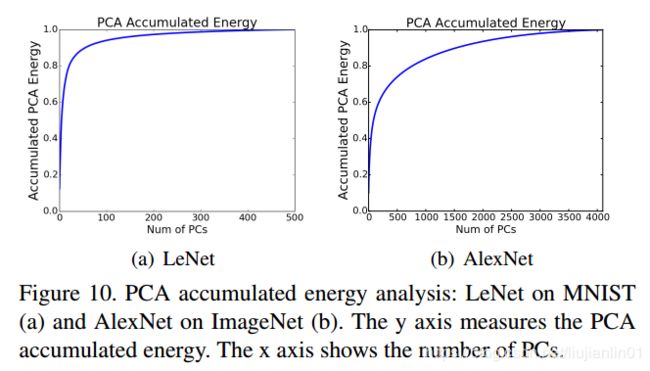
指导修剪比率选择的一种方法是对将要修剪的层的响应进行PCA累积能量分析[47]。
PCA累积能量分析显示该层需要多少台PC来捕获样本的大部分方差,这意味着我们应该为该层保留多少个神经元/卷积核。
我们在图10中显示LeNet(ip1)和AlexNet(fc7)的分类部分之前的最后FC层的PCA累积能量分析结果。
通过将方差阈值设置为0.95,LeNet需要500台PC中的120台,AlexNet需要2234个来捕获方差。
Experiments on AlexNet: Convolutional Layers v.s. FC Layers
从主要论文的实验中,我们发现FC层对精度损失,模型大小和内存使用有着显著影响。
为了探究修剪FC层和卷积层的影响,我们进行了修剪FC层和某些卷积层中一半神经元的实验。
我们将5个卷积层分为三个级别的特征提取器:低(Conv1-Conv2层),中(Conv3层)和高(Conv4-Conv5层)。
图11显示了学习曲线,并显示虽然FC层在AlexNet中很重要,但强大的局部特征提取器(卷积层中的更多内核)可以补偿FC层中修剪神经元的损失,甚至可以获得更好的预测能力(高曲线和低曲线)。

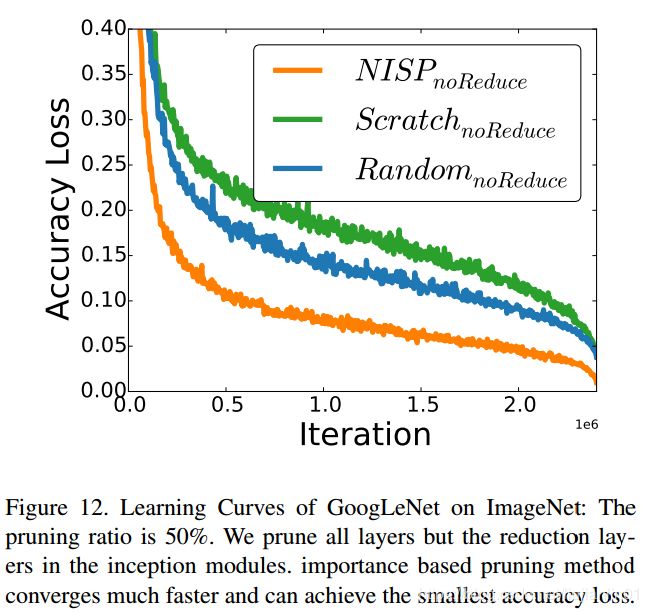
Experiments on GoogLeNet
“no_Reduce”(修剪所有的卷积层)的学习曲线如图12所示。
我们观察到基于重要性的修剪方法可以实现更好的初始化,更快的收敛和更小的最终精度损失。
Layer-wise Improvements
在我们在Titan X上的AlexNet实验中,中间层(除了卷积层和FC层之外的所有层)的计算时间占整个测试时间的17%。因此,在设计加速方法时也必须考虑这些层。
与现有方法相比,我们的优势之一是,由于每层的数据量或特征尺寸减小,网络中的所有层都可以加速。
例如,通过在卷积层中修剪内核,我们减少了当前层的输出通道和下一层的输入通道的数量。
理论上,假设修剪率为50%,除了输入通道无法修剪的第一层外,所有卷积层都可以加速4倍。
中间的池化层,非线性激活层和归一化层约具有2倍的理论加速比。
当所有卷积层和FC层的修剪比率为50%时,我们方法的分层加速比(理论和实验)如图13所示。
我们观察到对于池化层,非线性激活层和归一化层而言,理论加速和实验加速几乎相同。


