【机器学习实战-python3】树回归
本篇的数据和代码参见:https://github.com/stonycat/ML-in-Action
本篇博客部分参考Forec blog
一、数据建模问题
前面介绍了贪心算法的决策树,构建算法是ID3,每次选取当前最佳特征来分割数据,并且按照这个特征的所有可能取值来划分,一旦切分完成,这个特征在之后的执行过程中不会再有任何用处。这种方法切分过于迅速,并且需要将连续型数据离散化后才能处理,这样就破坏了连续变量的内在性质。
二元切分法是另一种树构建算法,每次将数据集切分成两半,如果数据的某个特征满足这个切分的条件,就将这些数据放入左子树,否则右子树。CART(Classification And Regression Trees,分类回归树)使用二元切分来处理连续型变量,并用总方差取代香农熵来分析模型的效果。
使用字典存储树的数据结构,每个节点包含以下四个元素:待切分的特征、待切分的特征值、左子树、右子树。
创建树的代码可以重用,伪代码大致如下。
找到最佳的待切分特征:
如果该节点不能再分,将该节点存为叶节点
执行二元切分
在左右子树分别递归调用
二、创建回归树
binSplitDataSet通过数组过滤切分数据集,createTree递归建立树,输入参数决定树的类型,leafType给出建立叶节点的函数,因此该参数也决定了要建立的是模型树还是回归树,errType代表误差计算函数,ops是一个包含树构建所需的其他参数的元组。
from numpy import *
#载入数据
def loadDataSet(fileName):
dataMat = []
fr = open(fileName)
for line in fr.readlines():
curLine = line.strip().split('\t')
# python3不适用:fltLine = map(float,curLine) 修改为:
fltLine = list(map(float, curLine))#将每行映射成浮点数,python3返回值改变,所以需要
dataMat.append(fltLine)
return dataMat
#切分数据集为两个子集
def binSplitDataSet(dataSet, feature, value): #数据集 待切分特征 特征值
mat0 = dataSet[nonzero(dataSet[:, feature] > value)[0], :]
mat1 = dataSet[nonzero(dataSet[:, feature] <= value)[0], :]
#下面原书代码报错 index 0 is out of bounds,使用上面两行代码
#mat0 = dataSet[nonzero(dataSet[:, feature] > value)[0], :][0]
#mat1 = dataSet[nonzero(dataSet[:, feature] <= value)[0], :][0]
return mat0, mat1
#Tree结点类型:回归树
def regLeaf(dataSet):#生成叶结点,在回归树中是目标变量特征的均值
return mean(dataSet[:,-1])
#误差计算函数:回归误差
def regErr(dataSet):#计算目标的平方误差(均方误差*总样本数)
return var(dataSet[:,-1]) * shape(dataSet)[0]
#二元切分
def chooseBestSplit(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):
#切分特征的参数阈值,用户初始设置好
tolS = ops[0] #允许的误差下降值
tolN = ops[1] #切分的最小样本数
#若所有特征值都相同,停止切分
if len(set(dataSet[:,-1].T.tolist()[0])) == 1:#倒数第一列转化成list 不重复
return None,leafType(dataSet) #如果剩余特征数为1,停止切分1。
# 找不到好的切分特征,调用regLeaf直接生成叶结点
m,n = shape(dataSet)
S = errType(dataSet)#最好的特征通过计算平均误差
bestS = inf; bestIndex = 0; bestValue = 0
for featIndex in range(n-1): #遍历数据的每个属性特征
# for splitVal in set(dataSet[:,featIndex]): python3报错修改为下面
for splitVal in set((dataSet[:, featIndex].T.A.tolist())[0]):#遍历每个特征里不同的特征值
mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal)#对每个特征进行二元分类
if (shape(mat0)[0] < tolN) or (shape(mat1)[0] < tolN): continue
newS = errType(mat0) + errType(mat1)
if newS < bestS:#更新为误差最小的特征
bestIndex = featIndex
bestValue = splitVal
bestS = newS
#如果切分后误差效果下降不大,则取消切分,直接创建叶结点
if (S - bestS) < tolS:
return None,leafType(dataSet) #停止切分2
mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue)
#判断切分后子集大小,小于最小允许样本数停止切分3
if (shape(mat0)[0] < tolN) or (shape(mat1)[0] < tolN):
return None, leafType(dataSet)
return bestIndex,bestValue#返回特征编号和用于切分的特征值
#构建tree
def createTree(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):
#数据集默认NumPy Mat 其他可选参数【结点类型:回归树,误差计算函数,ops包含树构建所需的其他元组】
feat,val = chooseBestSplit(dataSet, leafType, errType, ops)
if feat == None: return val #满足停止条件时返回叶结点值
#切分后赋值
retTree = {}
retTree['spInd'] = feat
retTree['spVal'] = val
#切分后的左右子树
lSet, rSet = binSplitDataSet(dataSet, feat, val)
retTree['left'] = createTree(lSet, leafType, errType, ops)
retTree['right'] = createTree(rSet, leafType, errType, ops)
return retTree
测试代码前,有三处错误:
1、TypeError: unsupported operand type(s) for /: ‘map‘ and ‘int‘
修改loadDataSet函数某行为fltLine = list(map(float,curLine)),因为python3中map的返回值变了,所以要加list()
2、TypeError: unhashable type: ‘matrix’
修改chooseBestSplit函数某行为:for splitVal in set((dataSet[:,featIndex].T.A.tolist())[0]): matrix类型不能被hash。
3、TypeError: index 0 is out of bounds
函数修改两行binSplitDataSet
mat0 = dataSet[nonzero(dataSet[:, feature] > value)[0], :]
mat1 = dataSet[nonzero(dataSet[:, feature] <= value)[0], :]
然后可以测试成功:
>>> reload(regTrees)
>>> from numpy import *
>>> myDat = mat(regTrees.loadDataSet('ex00.txt'))
>>> regTrees.createTree(myMat)
{'spInd': 0, 'spVal': 0.48813, 'right': -0.044650285714285719, 'left': 1.0180967672413792}
>>> myDat1 = mat(regTrees.loadDataSet('ex0.txt'))
>>> regTrees.createTree(myDat1)
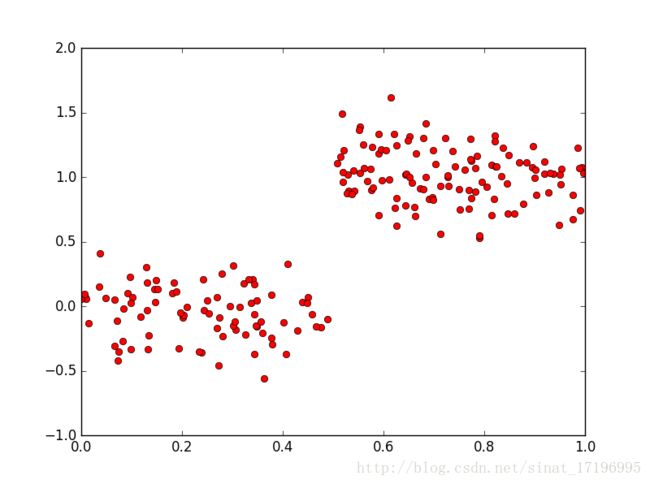
{'spInd': 1, 'spVal': 0.39435, 'right': {'spInd': 1, 'spVal': 0.197834, 'right': -0.023838155555555553, 'left': 1.0289583666666666}, 'left': {'spInd': 1, 'spVal': 0.582002, 'right': 1.980035071428571, 'left': {'spInd': 1, 'spVal': 0.797583, 'right': 2.9836209534883724, 'left': 3.9871631999999999}}}绘制两个ex0和ex00两个切分后的数据点图:
ex00.txt
import matplotlib.pyplot as plt
myDat=regTrees.loadDataSet(‘ex00.txt’)
myMat=mat(myDat)
regTrees.createTree(myMat)
plt.plot(myMat[:,0],myMat[:,1],’ro’)
plt.show()
import matplotlib.pyplot as plt
myDat1=regTrees.loadDataSet(‘ex00.txt’)
myMat1=mat(myDat1)
regTrees.createTree(myMat1)
plt.plot(myMat1[:,1],myMat1[:,2],’ro’)
plt.show()
三、树剪枝
如果树节点过多,则该模型可能对数据过拟合,通过降低决策树的复杂度来避免过拟合的过程称为剪枝。在上面函数chooseBestSplit中的三个提前终止条件是“预剪枝”操作,另一种形式的剪枝需要使用测试集和训练集,称作“后剪枝”。
使用后剪枝方法需要将数据集交叉验证,首先给定参数,使得构建出的树足够复杂,之后从上而下找到叶节点,判断合并两个叶节点是否能够取得更好的测试误差,如果是就合并。
#判断输入是否为一棵树
def isTree(obj):
return (type(obj).__name__=='dict') #判断为字典类型返回true
#返回树的平均值
def getMean(tree):
if isTree(tree['right']):
tree['right'] = getMean(tree['right'])
if isTree(tree['left']):
tree['left'] = getMean(tree['left'])
return (tree['left']+tree['right'])/2.0
#树的后剪枝
def prune(tree, testData):#待剪枝的树和剪枝所需的测试数据
if shape(testData)[0] == 0: return getMean(tree) # 确认数据集非空
#假设发生过拟合,采用测试数据对树进行剪枝
if (isTree(tree['right']) or isTree(tree['left'])): #左右子树非空
lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
if isTree(tree['left']): tree['left'] = prune(tree['left'], lSet)
if isTree(tree['right']): tree['right'] = prune(tree['right'], rSet)
#剪枝后判断是否还是有子树
if not isTree(tree['left']) and not isTree(tree['right']):
lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
#判断是否merge
errorNoMerge = sum(power(lSet[:, -1] - tree['left'], 2)) + \
sum(power(rSet[:, -1] - tree['right'], 2))
treeMean = (tree['left'] + tree['right']) / 2.0
errorMerge = sum(power(testData[:, -1] - treeMean, 2))
#如果合并后误差变小
if errorMerge < errorNoMerge:
print("merging")
return treeMean
else:
return tree
else:
return tree四、模型树
采用树结构对数据建模,除了将叶节点设定为常数,也可将其设为分段线性函数。 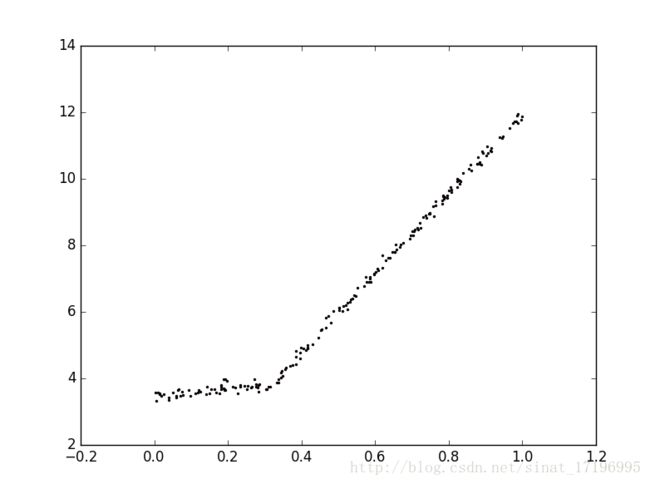
如上图所示,用两条直线肯定比一组常数model效果更好,可以由0.0~0.3和0.3~1.0的两条直线组成。决策树相比其他机器学习算法易于理解,而模型树的可解释性是它优于回归树的特性之一。模型树同时具备更高的预测准确度。
前面的代码已经给出了构建树的代码,只要修改参数errType和leafType。对于给定的数据集,先用现行的模型对它进行拟合,然后计算真实目标值和模型预测值之间的差距。最后求这些差值的平方和作为误差。
#模型树
def linearSolve(dataSet): #将数据集格式化为X Y
m,n = shape(dataSet)
X = mat(ones((m,n))); Y = mat(ones((m,1)))
X[:,1:n] = dataSet[:,0:n-1]; Y = dataSet[:,-1]
xTx = X.T*X
if linalg.det(xTx) == 0.0: #X Y用于简单线性回归,需要判断矩阵可逆
raise NameError('This matrix is singular, cannot do inverse,\n\
try increasing the second value of ops')
ws = xTx.I * (X.T * Y)
return ws,X,Y
def modelLeaf(dataSet):#不需要切分时生成模型树叶节点
ws,X,Y = linearSolve(dataSet)
return ws #返回回归系数
def modelErr(dataSet):#用来计算误差找到最佳切分
ws,X,Y = linearSolve(dataSet)
yHat = X * ws
测试结果可以看出,生成了y=3.468+1.185x和y=0.00169+11.964x两个线性模型。
与用于生成的数据相比(y=3.5+1.0x和y=0+12x)比较贴近
原始数据: 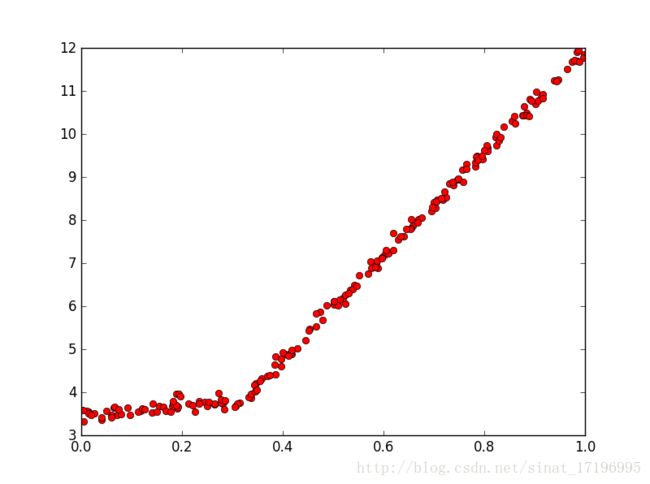
五、树回归和标准回归的比较
函数treeForeCast自顶向下遍历整棵树,直到命中叶节点为止。一旦到达叶节点,它会在输入数据上调用modelEval,该参数默认值是regTreeEval。要对回归树叶节点预测,就调用regTreeEval,要对模型树节点预测,调用modelTreeEval。
#用树回归进行预测
#1-回归树
def regTreeEval(model, inDat):
return float(model)
#2-模型树
def modelTreeEval(model, inDat):
n = shape(inDat)[1]
X = mat(ones((1, n + 1)))
X[:, 1:n + 1] = inDat
return float(X * model)
#对于输入的单个数据点,treeForeCast返回一个预测值。
def treeForeCast(tree, inData, modelEval=regTreeEval):#指定树类型
if not isTree(tree): return modelEval(tree, inData)
if inData[tree['spInd']] > tree['spVal']:
if isTree(tree['left']):#有左子树 递归进入子树
return treeForeCast(tree['left'], inData, modelEval)
else:#不存在子树 返回叶节点
return modelEval(tree['left'], inData)
else:
if isTree(tree['right']):
return treeForeCast(tree['right'], inData, modelEval)
else:
return modelEval(tree['right'], inData)
#对数据进行树结构建模
def createForeCast(tree, testData, modelEval=regTreeEval):
m = len(testData)
yHat = mat(zeros((m, 1)))
for i in range(m):
yHat[i, 0] = treeForeCast(tree, mat(testData[i]), modelEval)
return yHat自行车与智商的数据集分布:(数据纯属虚构。。) 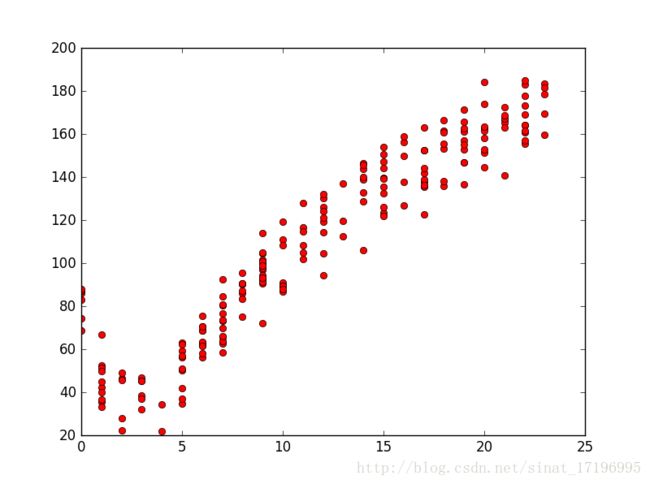
测试创建回归树 
创建模型树 
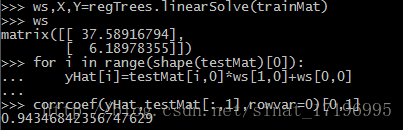
可以看出模型树误差更小。(更加接近1.0)
下面测试一下线性回归的效果,加入linearSolve函数:
#测试线性回归效果
def linearSolve(dataSet):
m,n = shape(dataSet)
X = mat(ones((m,n))); Y = mat(ones((m,1)))
X[:,1:n] = dataSet[:,0:n-1]; Y = dataSet[:,-1]
xTx = X.T*X
if linalg.det(xTx) == 0.0:
raise NameError('This matrix is singular, cannot do inverse,\n\
try increasing the second value of ops')
ws = xTx.I * (X.T * Y)
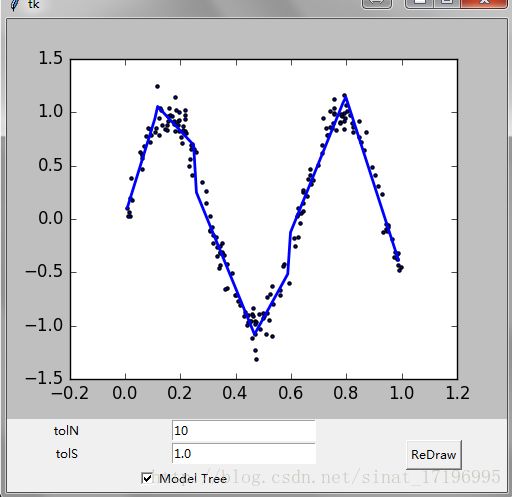
return ws,X,Y六、python Tkinter库创建GUI
机器学习从数据中提取有用的信息,能否将这些信息以易于人们理解的方式呈现非常重要。用户与数据交互的一种方式就是GUI。python有很多GUI框架,其中易于使用的是Tkiner,随python标准编译版本发布。
windows下python3.2版本之后是自动安装tkinter的,python3.3的引入方式为:
>>> import _tkinter
>>> import tkinter
>>> tkinter._test() #弹出测试窗口
>>>第一个小测试:
>>> root=Tk() #创建一个空的tk窗口,注意弹出后不要关闭,然后继续输入下一行
>>> myLabel=Label(root,text="hello,Tkinter!")
>>> myLabel=grid()#输入以上两行,框内显示文字
>>> #使程序完整:
>>> root.mainloop()这里简单介绍一下Tkinter:
Tkinter是由很多组件(Widget)组成的,包括文本框,按钮,标签(刚才用的Label)等。其中.grid()是把组件的放入一种二维表格的布局管理器中。默认0行0列。
下面将tk与matplotlib集成:
import regTrees
import matplotlib
matplotlib.use('TkAgg') #设置后端TkAgg
#将TkAgg和matplotlib链接起来
from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg
from matplotlib.figure import Figure
def reDraw(tolS, tolN):
reDraw.f.clf() #清空之前的图像
reDraw.a = reDraw.f.add_subplot(111)#重新添加新图
if chkBtnVar.get():#检查选框model tree是否被选中
if tolN < 2: tolN = 2
myTree = regTrees.createTree(reDraw.rawDat, regTrees.modelLeaf,regTrees.modelErr, (tolS, tolN))
yHat = regTrees.createForeCast(myTree, reDraw.testDat, regTrees.modelTreeEval)
else:
myTree = regTrees.createTree(reDraw.rawDat, ops=(tolS, tolN))
yHat = regTrees.createForeCast(myTree, reDraw.testDat)
reDraw.a.scatter(reDraw.rawDat[:, 0], reDraw.rawDat[:, 1], s=5) # 绘制真实值
reDraw.a.plot(reDraw.testDat, yHat, linewidth=2.0) # 绘制预测值
reDraw.canvas.show()
def getInputs():#获取输入
try:#期望输入是整数
tolN = int(tolNentry.get())
except:#清楚错误用默认值替换
tolN = 10
print("enter Integer for tolN")
tolNentry.delete(0, END)
tolNentry.insert(0, '10')
try:#期望输入是浮点数
tolS = float(tolSentry.get())
except:
tolS = 1.0
print("enter Float for tolS")
tolSentry.delete(0, END)
tolSentry.insert(0, '1.0')
return tolN, tolS
def drawNewTree():
tolN, tolS = getInputs() # 从输入文本框中获取参数
reDraw(tolS, tolN) #绘制图下面为布局GUI代码:
root = Tk()
reDraw.f = Figure(figsize=(5, 4), dpi=100) # 创建画布
reDraw.canvas = FigureCanvasTkAgg(reDraw.f, master=root)
reDraw.canvas.show()
reDraw.canvas.get_tk_widget().grid(row=0, columnspan=3)
Label(root, text="tolN").grid(row=1, column=0)
tolNentry = Entry(root)
tolNentry.grid(row=1, column=1)
tolNentry.insert(0, '10')
Label(root, text="tolS").grid(row=2, column=0)
tolSentry = Entry(root)
tolSentry.grid(row=2, column=1)
tolSentry.insert(0, '1.0')
Button(root, text="ReDraw", command=drawNewTree).grid(row=1, column=2, rowspan=3)
chkBtnVar = IntVar()
chkBtn = Checkbutton(root, text="Model Tree", variable=chkBtnVar)
chkBtn.grid(row=3, column=0, columnspan=2)
reDraw.rawDat = mat(regTrees.loadDataSet('sine.txt'))
reDraw.testDat = arange(min(reDraw.rawDat[:, 0]), max(reDraw.rawDat[:, 0]), 0.01)
reDraw(1.0, 10)
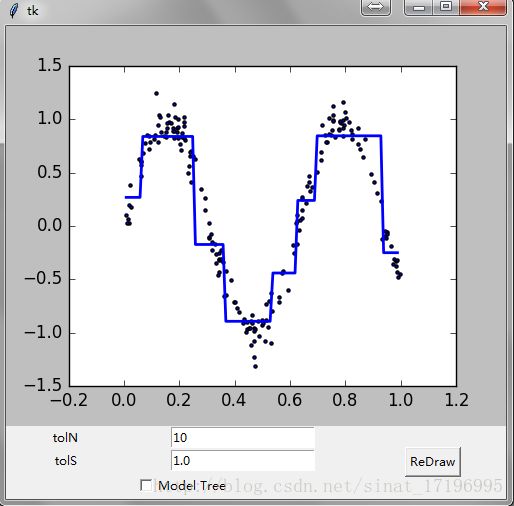
root.mainloop()测试,打开命令行直接输入:
python treeExplore.py
七、总结
数据集中会包含一些复杂的相互关系,使输入数据和目标变量之间存在非线性的关系。对于这种复杂关系的建模,可以采用树模型来对预测进行分段,包括分段常数(回归树)和分段直线(模型树)。
回归分类树CART算法用于构建二元树对离散/连续型数据进行切分。根据使用的不同误差准则方法,可以通过CART算法构建模型树和回归树。但是该算法构建的树倾向于过拟合,可采用剪枝的方法解决。剪枝方法分为预剪枝(在树的构建过程中人工设置参数预防过拟合)和后剪枝(树构建完毕进行删除/合并分支)。
Tkinter是python的一个最常用的GUI工具包,结合matplotlib可以构建更强大的GUI。