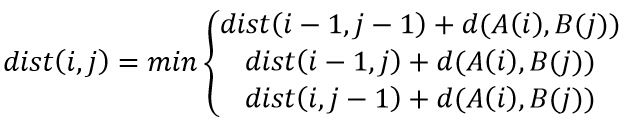离散序列的一致性度量方法:动态时间规整(DTW)
动态时间规整:Dynamic Time Warping(DTW),是一种衡量两个离散时间序列相似度的方法,主要特点是在序列长度不一或x轴无法完全对齐的情况下,用满足一定条件的的时间规整函数描述两者之间的时间对应关系。DTW算法在各种模式匹配任务中被广泛使用,如语音识别、动态手势识别和信息检索等中。
一、算法简述
在数字信号处理领域中,时间序列是数据的一种常见表示形式。对于时间序列处理来说,对于许多的信号处理任务,如图像匹配、视频跟踪和姿态识别等,通常需要度量两个离散序列的相似性。而这一步骤说难不难,说易也不易,这往往需要考虑信号采样、噪声干扰等实际问题。
在很多情况下,单纯的相似性度量方法无法很好度量两个序列的一致性,如在语音识别中经常出现两段时间序列的长度不相等的情况(或下图中的情况),此时从直观上都能观察到,直接使用欧几里得距离、相关系数等方法进行度量并不靠谱,此时点对点运算变得无意义。
DTW的主要思路如下:
1.假定两个待匹配的离散数据分别为A={A(1),A(2),…,A(m)}和B={B(1),B(2),…,B(m)},其中下标为1的元素为序列的起点,下标为m/n的元素为序列终点。
2.为了对齐A,B两个序列,这里采用了“动态规划”的方法,首先构造一个m*n的矩阵,用于存放两序列点对点之间的距离(一般可使用欧氏距离),距离越小表明两点之间的相似度越高。
3.该部分是DTW算法的核心,这里把矩阵看成一个网格,算法的目的可总结为寻找一条通过此矩阵网格的最优路径,该路径通过的网格点即为两个离散序列经过对齐后的点对。
4.找到最优路径后,DTW算法定义了一个归整路径距离(Warp Path Distance),通过使用所有相似点之间距离的和,来衡量两个时间序列之间的相似性。
二、归整路径距离计算方法:
计算归整路径(Warp Path)。其形式可表示为:W={w1,w2,…,wK}。其中wk的形式为(i,j),其中i表示的是X中的i坐标,j表示的是Y中的j坐标。
![]()
这条路径不是随意选择的,需要满足以下几个约束:
1.边界条件:w1=(1, 1)和wK=(m, n)。
2.连续性:如果wk-1=(i,j),那么对于路径的下一个点wk=(i’,j’)需要满足:(i’-i)<=1和 (j’-j)<=1。因此只能和自己相邻的点对齐。这样可以保证序列A和B中的每个元素都在规整路径W中出现。
3.单调性:如果wk-1=(i,j),那么对于路径的下一个点wk=(i’,j’)需要满足:(i’-i)>=0和(j’-j)>=0。在这里需要假设A和B的顺序均是不可改变的。因此路径W在矩阵网格中的走势必须是随着时间单调递增的,如下图所示,整个过程是从矩阵网格的左下角出发,在右上角结束。
基于以上3个约束,规整路径的计算被简化为三种情况:
最后,需要定义一个累加距离dist,即从(0,0)点开始匹配两个序列A和B,每到一个点,之前所有的点计算的距离都会累加。到达终点(n,m)后,这个累积距离就描述了序列A和B的总体相似程度。累积距离dist(i,j)可以表示成以下公式:
其中,累积距离dist(i,j)为当前格点的距离d(A(i),B(j)),也就是两个序列A,B中的对应两点A(i)和B(j)的欧式距离与到达该点的最小的邻近元素的累积距离之和。
三、一个具体例子
参考:http://www.cnblogs.com/tornadomeet/archive/2012/03/23/2413363.html
四、Matlab代码实现
% 输入两段离散序列,输出两段序列的总欧式距离
function dist = dtw(t,r)
n = size(t,1);
m = size(r,1);
d = zeros(n,m);
for i = 1:n
for j = 1:m
d(i,j) = (t(i,:)-r(j,:)).^2;
end
end
D = ones(n,m) * realmax;
D(1,1) = d(1,1);
for i = 1:n
for j = 1:m
if i==1&&j==1
continue;
end
if i>1
D1 = D(i-1,j);
else
D1 = realmax;
end
if j>1&&i>1
D2 = D(i-1,j-1);
else D2 = realmax;
end
if j>1
D3 = D(i,j-1);
else
D3 = realmax;
end
D(i,j) = d(i,j) + min([D1,D2,D3]);
end
end
dist = D(n,m);五、参考链接和资料
http://blog.csdn.net/zouxy09/article/details/9140207
http://www.cnblogs.com/tornadomeet/archive/2012/03/23/2413363.html
http://www.baike.com/wiki/dtw
参考文献:Eamonn J. Keogh, Derivative Dynamic Time Warping