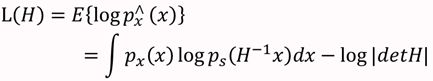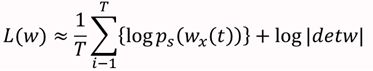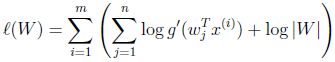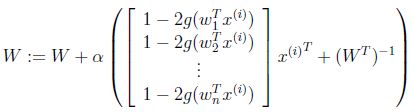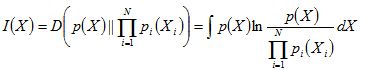【机器学习】ICA算法简介
转自:https://blog.csdn.net/lg1259156776/article/details/51132160
ICA算法的研究可分为基于信息论准则的迭代估计方法和基于统计学的代数方法两大类,从原理上来说,它们都是利用了源信号的独立性和非高斯性。基于信息论的方法研究中,各国学者从最大熵、最小互信息、最大似然和负熵最大化等角度提出了一系列估计算法。如FastICA算法, Infomax算法,最大似然估计算法等。基于统计学的方法主要有二阶累积量、四阶累积量等高阶累积量方法。
一:最大似然估计算法
1.1 目标函数部分
我们假设信号Si有概率密度函数Ps(t),由于我们假定信号源是相互独立的,其实经过白化处理后就变成独立的了;那么在给定时刻的联合分布函数为:
知道了信号源的联合分布Ps(t),再由分解矩阵S=WX,可以得出信号x的联合分布函数。
其中|W|为W的行列式。
由于没有先验知识,只知道原信号之间特征独立,且最多有一个是高斯分布,所以我们没有办法确定Ps(t)的分布,所以我们选取一个概率密度函数Ps^(t)来近似估计Ps(t)。
在概率论中我们知道概率密度函数由累积分布函数F(x)(cumulative distribution function,cdf)求导得到。
F(x)要满足两个性质:1,单调递增;2,值域在[0 1]范围
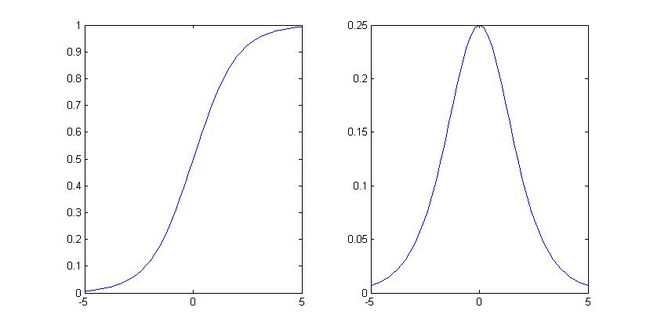
我们发现sigmoid函数的定义域是负无穷到正无穷,值域为0到1,缓慢递增的性质。基于sigmoid函数良好的性质,我们用sigmoid函数来近似估计F(x),通过求导得到Ps^(t)。
两函数图像如图:
怎么感觉pdf 函数g(s)这么像高斯分布函数呢??这个有点不理解(以后在研究吧)。
如果我们预先知道Ps(t)的分布函数,那就不用假设了;但是在缺失的情况下,sigmoid函数大多数情况下能够起到不错的效果。由于Ps(t)s是个对称函数,所以均值E[s]=0,那么E[x]=E[AS]=0,x的均值也是0。
知道了Ps(t),就剩下W了,在给定训练样本{Xi(Xi1,Xi2,........Xin),i=1,2....m个样本,样本的对数似然估计如下:
T=m为独立同分布观测数据的样本数。最大化此似然函数就可获得关于参数W 的最佳估计。
1.2 优化部分(梯度下降算法)
接下来就是对W求导了,这里牵涉一个问题是对行列式|W|进行求导的方法,属于矩阵微积分
![]()
最终得到的求导后公式如下,logg'(s)的导数为1-2g(s)(可以自己验证):
当迭代求出W后,便可得到S=WX来还原出原始信号.
注意:我们计算最大似然估计时,假设了Xi与Xj之间是独立的,然而对于语音信号或者其他具有时间连续依赖特性(比如温度)上,这个假设不能成立。但是在数据足够多时,假设独立对效果影响不大,同时如果事先打乱样例,并运行随机梯度上升算法,那么能够加快收敛速度。
二:负熵最大的FastICA算法
2.1目标函数部分
2.1.1负熵判别准则
由极大熵原理可知,在方差相同的条件下,所有概率分布中,高斯分布的熵最大;因而我们可以利用熵来度量分布的非高斯性。
因此通过度量分离结果的非高斯性,作为分离结果独立性的度量;当非高斯性达到最大时,表明已完成对各个分量的分离。
因为FastICA算法以负熵最大作为一个搜寻方向,因此先讨论一下负熵判决准则。由信息论理论可知:在所有等方差的随机变量中,高斯变量的熵最大,因而我们可以利用熵来度量非高斯性,常用熵的修正形式,即负熵。
负熵的定义:![]() 其中XG是和X具有相同协方差的随机变量,H()为变量的微分熵
其中XG是和X具有相同协方差的随机变量,H()为变量的微分熵
联系极大熵原理,XG为高斯分布,所以J(X)>=0;当且仅当X本身也为高斯分布时=0;所以J(x)的值越大,证明X的非高斯性越强,
2.1.2负熵与独立性关系
假设n维随机变量X=[X1,X2……Xn],其互信息为I(X):
互信息即为:独立分布乘积分布与联合分布之间的负熵J(X),当Xi相互独立时,互信息为0;
由于计算J(X)需要联合分布函数和各个分量的分布函数,,这个显然不切实际;所以采用非线性变换g(x)后的均值期望来近似替代。
其中g(x)可以为:g(x)=tanh(a*x),g(x)=x^3;g(x)=x*exp(-x^2/2) (为啥我也不清楚,都是对称的奇函数)
由于Xi即为观测数据X分离后的独立变量Si,再由中心极限定理可知,若随机变量X有许多相互独立的随机变量信号源Si相互组合而成,则不论Si为何种分布,观测变量数据X比Si具有更强的高斯性,换言之Xi的非高斯性更强。
所以,负熵J(X)的值越小,即此时的互信息I(X)越小,此时分离的变量Si独立性越好。
2.2 优化部分
快速ICA算法是找一个方向以便WX具有最大的非高斯性,也即最大的相互独立性;这里的独立性通过负熵来给出,通过均值近似估计来计算。这里通过白化处理,使W的范数为1,即使WX的方差估计为1;
优化过程推导比较复杂,公式太多就通过截图给出吧!
实践中,FastICA算法中用的期望必须用它们的估计值代替。当然最好的估计是相应的样本平均。理想情况下,所有的有效数据都应该参与计算,但这会降低计算速度。所以通常用一部分样本的平均来估计,样本数目的多少对最后估计的精确度有很大影响。迭代中的样本点应该分别选取,假如收敛不理想的话,可以增加样本的数量。
三:MATLAB源程序及说明
%下程序为ICA的调用函数,输入为观察的信号,输出为解混后的信号
function Z=ICA(X)
%-----------去均值---------
[M,T] = size(X); %获取输入矩阵的行/列数,行数为观测数据的数目,列数为采样点数
average=mean(X')'; %均值
for i=1:M
X(i,:)=X(i,:)-average(i)*ones(1,T);
end
%---------白化/球化------
Cx =cov(X',1); %计算协方差矩阵Cx
[eigvector,eigvalue]= eig(Cx); %计算Cx的特征值和特征向量
W=eigvalue^(-1/2)*eigvector'; %白化矩阵
Z=W*X; %正交矩阵
%----------迭代-------
Maxcount=10000; %最大迭代次数
Critical=0.00001; %判断是否收敛
m=M; %需要估计的分量的个数
W=rand(m);
for n=1:m
WP=W(:,n); %初始权矢量(任意)
% Y=WP'*Z;
% G=Y.^3;%G为非线性函数,可取y^3等
% GG=3*Y.^2; %G的导数
count=0;
LastWP=zeros(m,1);
W(:,n)=W(:,n)/norm(W(:,n));
whileabs(WP-LastWP)&abs(WP+LastWP)>Critical
count=count+1; %迭代次数
LastWP=WP; %上次迭代的值
% WP=1/T*Z*((LastWP'*Z).^3)'-3*LastWP;
for i=1:m
WP(i)=mean(Z(i,:).*(tanh((LastWP)'*Z)))-(mean(1-(tanh((LastWP))'*Z).^2)).*LastWP(i);
end
WPP=zeros(m,1);
for j=1:n-1
WPP=WPP+(WP'*W(:,j))*W(:,j);
end
WP=WP-WPP;
WP=WP/(norm(WP));
if count==Maxcount
fprintf('未找到相应的信号);
return;
end
end
W(:,n)=WP;
end
Z=W'*Z;
%以下为主程序,主要为原始信号的产生,观察信号和解混信号的作图
clear all;clc;
N=200;n=1:N;%N为采样点数
s1=2*sin(0.02*pi*n);%正弦信号
t=1:N;s2=2*square(100*t,50);%方波信号
a=linspace(1,-1,25);s3=2*[a,a,a,a,a,a,a,a];%锯齿信号
s4=rand(1,N);%随机噪声
S=[s1;s2;s3;s4];%信号组成4*N
A=rand(4,4);
X=A*S;%观察信号
%源信号波形图
figure(1);subplot(4,1,1);plot(s1);axis([0N -5,5]);title('源信号');
subplot(4,1,2);plot(s2);axis([0N -5,5]);
subplot(4,1,3);plot(s3);axis([0N -5,5]);
subplot(4,1,4);plot(s4);xlabel('Time/ms');
%观察信号(混合信号)波形图
figure(2);subplot(4,1,1);plot(X(1,:));title('观察信号(混合信号)');
subplot(4,1,2);plot(X(2,:));
subplot(4,1,3);plot(X(3,:));subplot(4,1,4);plot(X(4,:));
Z=ICA(X);
figure(3);subplot(4,1,1);plot(Z(1,:));title('解混后的信号');
subplot(4,1,2);plot(Z(2,:));
subplot(4,1,3);plot(Z(3,:));
subplot(4,1,4);plot(Z(4,:));xlabel('Time/ms');
参考文献:
1:http://wenku.baidu.com/view/941f6782e53a580216fcfe03.html
2:http://wenku.baidu.com/view/8fa7f71b6bd97f192279e9aa.html
3:http://wenku.baidu.com/view/d362d8330b4c2e3f57276387.html
其他的一些关于ICA的介绍:
https://blog.csdn.net/sinat_27763257/article/details/80568792