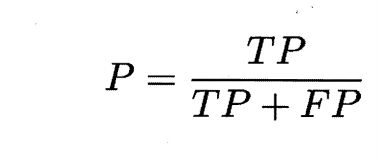自然语言处理学习

Task1

Anaconda安装

很久以前就安装了，而且Anaconda安装没有什么难点。随便搜一下就有很多文章讲述。贴一个别人的链接可以看一下。
https://blog.csdn.net/u012318074/article/details/77075209

Conda学习

下面是一些常用的语法

conda info #查询conda信息
conda update conda #升级conda
conda update anaconda #升级anaconda
conda update python 升级python
conda create --name [name] [dependent package list] #创建环境
#例： conda create --name mypython2

#激活环境
    •   Linux and macOS: source activate snowflakes
    •   Windows: activate snowflakes

conda info --envs #列出当前的所有环境

conda remove --name mypython2 --all #删除指定的环境

1、查询可用包版本信息
conda search --full-name python
conda search beautifulsoup4


查询在线包链接：
https://anaconda.org/

2、查询当前环境中的包列表
conda list

3、在环境中安装包
conda install numpy=1.13.3
conda install --name [环境名称] beautifulsoup4

python编辑器安装与学习

刚开始喜欢用pycharm,现在基本上使用jupyter notebook，感觉使用起来更方便一些。
网上教程很多，就不多说了。

Tensorflow 库安装与学习

刚开始安装的是cpu版本的，后来重装了一个gpu版本的，gpu版本的话要有支持的显卡，然后装cuda和cudnn,麻烦一些，但是cpu版本的只能跑一些简单的代码，想深入学习的话，最好装gpu版本的。安装教程可以看下面的链接。
https://blog.csdn.net/u012692537/article/details/80432184
tensorflow有自己的语法，需要多敲才能记住。推荐《TensorFlow实战Google深度学习框架》这本书。

Reference

https://www.jianshu.com/p/ddf06e8a24fd

Task2

THUCNews数据集

THUCNews是根据新浪新闻RSS订阅频道2005~2011年间的历史数据筛选过滤生成，包含74万篇新闻文档（2.19 GB），均为UTF-8纯文本格式。我们在原始新浪新闻分类体系的基础上，重新整合划分出14个候选分类类别：财经、彩票、房产、股票、家居、教育、科技、社会、时尚、时政、体育、星座、游戏、娱乐。
THUCNews中文数据集包括四个文件：cnews.train.txt、cnews.val.txt、cnews.test.txt 和 cnews.vocab.txt
cnews.train.txt是训练数据，cnews.val.txt是验证数据，cnews.test.txt是测试数据，这三个文件每条数据都是一段新闻文本和新闻所属类别，cnews.vocab.txt是词汇表、字符集。

IMDB数据集

主要包含train和test文件夹，里面的pos和neg文件夹下是积极的和消极的评论文本，train文件夹下还有unsup文件夹，内有50000条没有标记的文本。

准确率(Precision)

假定有一个二分类任务，正类和负类，对测试数据进行预测，结果可以分成四种。

TP(True Positive): 原本是正类，预测结果为正类。(正确预测为正类)
FP(False Positive): 原本是负类，预测结果为正类。(错误预测为正类)
TN(True Negative): 原本是负类，预测结果为负类。(正确预测为负类)
FN(False Negative): 原本是正类，预测结果为负类。(错误预测为负类)

基于上述概念，可以引出准确率和召回率。
准确率(Precision)
对于给定的测试数据集,预测结果为正类的数据中，有多少数据被正确预测，即

    P=TP/(TP+FP)

召回率(Recall)

召回率是覆盖面的度量，度量有多个正例被分为正例

R=TP/(TP+FN)

PR曲线

P-R曲线刻画准确率和召回率之间的关系，准确率和召回率是一对矛盾的度量，一般来说，准确率高时，召回率往往偏低，召回率高时，准确率往往偏低。
在很多情况下，我们可以根据学习器的预测结果对样例进行排序，排在前面的是学习器认为最可能是正例的样本，排在后面的是学习器认为最不可能是正例的样本，按此顺序逐个把样本作为正例进行预测，则每次可计算当前的准确率和召回率，以准确率为纵轴，以召回率为横轴，可以画出下面的P-R曲线。

上图来自西瓜书，查准率即准确率，查全率即召回率。

如果一个学习器的P-R曲线被另一个学习器的P-R曲线完全包住，则可断言后者的性能优于前者，例如上面的A和B优于学习器C，但是A和B的性能无法直接判断，但我们往往仍希望把学习器A和学习器B进行一个比较，我们可以根据曲线下方的面积大小来进行比较，但更常用的是平衡点。平衡点（BEP）是查准率=查全率时的取值，如果这个值较大，则说明学习器的性能较好。所以基于平衡点，可以认为学习器A优于B。

ROC曲线和AUC

很多学习器是为测试样本产生一个实值或概率预测，然后将这个预测值与一个分类阈值进行比较，若大于阈值分为正类，否则为反类，因此分类过程可以看作选取一个截断点。
不同任务中，可以选择不同截断点，若更注重”准确率”，应选择排序中靠前位置进行截断，反之若注重”召回率”，则选择靠后位置截断。因此排序本身质量的好坏，可以直接导致学习器不同泛化性能好坏，ROC曲线则是从这个角度出发来研究学习器的工具。
ROC全称是"受试者工作特征（Receiver Operating Characteristic）",ROC曲线的坐标轴分别为真正例率（TPR）和假正例率（FPR），TPR为纵轴，FPR为横轴，定义如下：


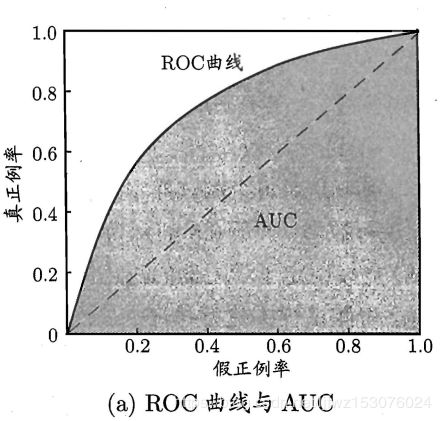
在进行学习器比较时，和P-R图类似，若一个学习器的ROC曲线完全"包住"另一个学习器的ROC曲线，则说明前者的性能更好，若二者的ROC曲线发生交叉，则难以一般性的断言二者孰优孰劣。这时可以通过比较ROC曲线下的面积，即AUC(Area Under of ROC Curve)，如上图阴影部分面积。

Task3

分词

中文分词

中文分词是中文信息处理的基本技术，指将一个汉字序列切分成一个个单独的词。分词就是将连续的字序列按照一定的规范重新组合成词序列的过程。
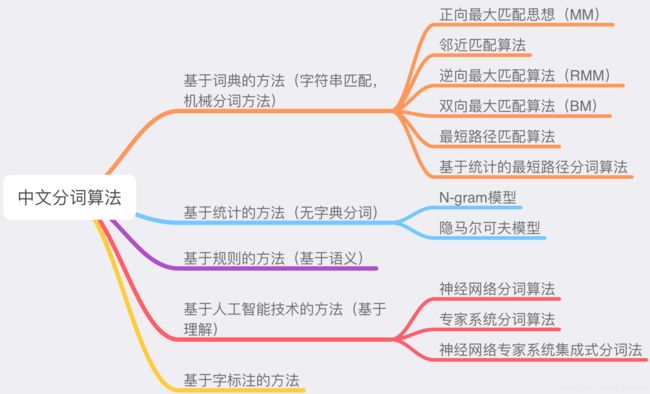
现有的中文分词算法有五大类：基于词典的分词方法，基于统计的分词方法，基于规则的分词方法，基于字标注的分词方法，基于人工智能技术（基于理解）的分词方法。

正向最大匹配算法（MM）

MM的步骤是：

（1）从左向右取待分汉语句的m个字作为匹配字段，m为词典中最长词的长度。

（2）查找词典进行匹配。

（3）若匹配成功，则将该字段作为一个词切分出去。

（4）若匹配不成功，则将该字段最后一个字去掉，剩下的字作为新匹配字段，进行再次匹配。

（5）重复上述过程，直到切分所有词为止。

逆向最大匹配法（RMM）

RMM的基本原理与FMM基本相同，不同的是分词的方向与FMM相反。RMM是从待分词句子的末端开始，也就是从右向左开始匹配扫描，每次取末端m个字作为匹配字段，匹配失败，则去掉匹配字段前面的一个字，继续匹配。

双向最大匹配法（Bi-MM）

Bi-MM是将正向最大匹配法得到的分词结果和逆向最大匹配法得到的结果进行比较，然后按照最大匹配原则，选取词数切分最少的作为结果。据SunM.S.和Benjamin K.T.（1995）的研究表明，中文中90.0%左右的句子，正向最大匹配法和逆向最大匹配法完全重合且正确，只有大概9.0%的句子两种切分方法得到的结果不一样，但其中必有一个是正确的（歧义检测成功），只有不到1.0%的句子，使用正向最大匹配法和逆向最大匹配法的切分虽然重合但是错的，或者两种方法切分不同但结果都不对（歧义检测失败）。

双向最大匹配的规则是：

（1）如果正反向分词结果词数不同，则取分词数量少的那个。

（2）如果分词结果词数相同：

        1）分词结果相同，没有歧义，返回任意一个。

        2）分词结果不同，返回其中单字数量较少的那个。

举个栗子：使用上述三种分词方法对"研究生命的起源"一句进行分词得到下面的结果
MM: 研究生 / 命 / 的 / 起源
FMM:研究 / 生命 / 的 / 起源
Bi-MM:研究 / 生命 / 的 / 起源

词频字符频率统计

可以使用collections.Counter模块，字符频率统计示例代码如下：

import numpy as np
from collections import Counter

word="就个人而言如果有那一天真的是写不动代码了，就会选择停下来研究古文言文历史，探索历史里面未知的秘密。"
result=Counter(word)
print(result)

结果为：

Counter({'就': 2, '言': 2, '的': 2, '，': 2, '文': 2, '历': 2, '史': 2, '个': 1, '人': 1, '而': 1, '如': 1, '果': 1, '有': 1, '那': 1, '一': 1, '天': 1, '真': 1, '是': 1, '写': 1, '不': 1, '动': 1, '代': 1, '码': 1, '了': 1, '会': 1, '选': 1, '择': 1, '停': 1, '下': 1, '来': 1, '研': 1, '究': 1, '古': 1, '探': 1, '索': 1, '里': 1, '面': 1, '未': 1, '知': 1, '秘': 1, '密': 1, '。': 1})

词频统计：

from collections import Counter
import jieba

word="就个人而言如果有那一天真的是写不动代码了，就会选择停下来研究古文言文历史，探索历史里面未知的秘密。"
seg_list = list(jieba.cut(word))
result = Counter(seg_list )
print(result)

结果为：

Counter({'就': 2, '，': 2, '历史': 2, '个人': 1, '而言': 1, '如果': 1, '有': 1, '那': 1, '一天': 1, '真的': 1, '是': 1, '写': 1, '不动': 1, '代码': 1, '了': 1, '会': 1, '选择': 1, '停下来': 1, '研究': 1, '古': 1, '文言文': 1, '探索': 1, '里面': 1, '未知': 1, '的': 1, '秘密': 1, '。': 1})

语言模型

上面一句话的二元模型（bigram）：

文本矩阵化

import jieba
import pandas as pd
import tensorflow as tf
from collections import Counter
from gensim.models import Word2Vec
from sklearn.feature_extraction.text import CountVectorizer
 
 
# 读取停用词
def read_stopword(filename):
    stopword = []
    fp = open(filename, 'r')
    for line in fp.readlines():
        stopword.append(line.replace('\n', ''))
    fp.close()
    return stopword
 
 
# 切分数据，并删除停用词
def cut_data(data, stopword):
    words = []
    for content in data['content']:
        word = list(jieba.cut(content))
        for w in list(set(word) & set(stopword)):
            while w in word:
                word.remove(w)
        words.append(' '.join(word))
    data['content'] = words
    return data
 
 
# 获取单词列表
def word_list(data):
    all_word = []
    for word in data['content']:
        all_word.extend(word)
    all_word = list(set(all_word))
    return all_word
 
 
# 计算文本向量
def text_vec(data):
    count_vec = CountVectorizer(max_features=300, min_df=2)
    count_vec.fit_transform(data['content'])
    fea_vec = count_vec.transform(data['content']).toarray()
    return fea_vec
 
 
if __name__ == '__main__':
    data = pd.read_csv('./data/cnews/cnews.test.txt', names=['title', 'content'], sep='\t')  # (10000, 2)
    data = data.head(50)
 
    stopword = read_stopword('./data/stopword.txt')
    data = cut_data(data, stopword)
 
    fea_vec = text_vec(data)
    print(fea_vec)

Task4

TF-IDF原理

TF-IDF(Term Frequency-Inverse Document Frequency, 词频-逆文件频率).
TF
词频，就是每个词在文本中出现的次数。
假设现在有一段文本
corpus=[“I come to China to travel”,
“This is a car polupar in China”,
"I love tea and Apple ",
“The work is to write some papers in science”]
不考虑停用词，处理后得到的词向量如下：

[[0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 2 1 0 0]
[0 0 1 1 0 1 1 0 0 1 0 0 0 0 1 0 0 0 0]
[1 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0]
[0 0 0 0 0 1 1 0 1 0 1 1 0 1 0 1 0 1 1]]

如果我们直接将统计词频后的19维特征做为文本分类的输入，会发现有一些问题。比如第一个文本，我们发现 “come” , “China” 和 “Travel” 各出现1次，而“to“出现了两次。似乎看起来这个文本与 ”to“ 这个特征更关系紧密。但是实际上”to“是一个非常普遍的词，几乎所有的文本都会用到，因此虽然它的词频为2，但是重要性却比词频为1的 “China” 和 “Travel” 要低的多。如果我们的向量化特征仅仅用词频表示就无法反应这一点。因此我们需要进一步的预处理来反应文本的这个特征，而这个预处理就是TF-IDF。
IDF
IDF即逆文本频率。在上面的例子中可以看到到几乎所有文本都会出现的"to"其词频虽然高，但是重要性却应该比词频低的"China"和“Travel”要低。我们的IDF就是来帮助我们来反应这个词的重要性的，进而修正仅仅用词频表示的词特征值。

概括来讲， IDF反应了一个词在所有文本中出现的频率，如果一个词在很多的文本中出现，那么它的IDF值应该低，比如上文中的“to”。而反过来如果一个词在比较少的文本中出现，那么它的IDF值应该高，说明词条具有很好的类别区分能力。
IDF的公式为：

将TF和IDF结合得到TF-IDF:

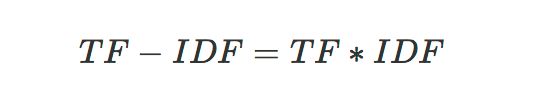
文本矩阵化

对英文数据集训练集的pos文件夹下前100个文件进行了文本矩阵化

from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
import os
import numpy as np
import pandas as pd

data_path='E:/dataset/aclImdb/train/pos'

train_list=os.listdir(data_path)
data=[]
for i in train_list[:100]:
    path=data_path+'/'+i
    data.append(open(path).readlines()[0])
vectorizer=CountVectorizer()

transformer = TfidfTransformer()
tfidf = transformer.fit_transform(vectorizer.fit_transform(data))  
print (tfidf)

一些输出：

互信息

两个离散随机变量 X 和 Y 的互信息可以定义为：

其中 p(x,y) 是 X 和 Y 的联合概率分布函数，而p(x)和p(y)分别是 X 和 Y 的边缘概率分布函数。
在连续随机变量的情形下，求和被替换成了二重定积分：

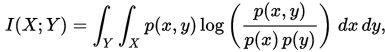
其中 p(x,y) 当前是 X 和 Y 的联合概率密度函数，而p(x)和p(y)分别是 X 和 Y 的边缘概率密度函数。

互信息量I(xi;yj)在联合概率空间P(XY)中的统计平均值。 平均互信息I(X;Y)克服了互信息量I(xi;yj)的随机性,成为一个确定的量。如果对数以 2 为基底，互信息的单位是bit。

直观上，互信息度量 X 和 Y 共享的信息：它度量知道这两个变量其中一个，对另一个不确定度减少的程度。例如，如果 X 和 Y 相互独立，则知道 X 不对 Y 提供任何信息，反之亦然，所以它们的互信息为零。在另一个极端，如果 X 是 Y 的一个确定性函数，且 Y 也是 X 的一个确定性函数，那么传递的所有信息被 X 和 Y 共享：知道 X 决定 Y 的值，反之亦然。因此，在此情形互信息与 Y（或 X）单独包含的不确定度相同，称作 Y（或 X）的熵。而且，这个互信息与 X 的熵和 Y 的熵相同。（这种情形的一个非常特殊的情况是当 X 和 Y 为相同随机变量时。）

互信息是 X 和 Y 联合分布相对于假定 X 和 Y 独立情况下的联合分布之间的内在依赖性。于是互信息以下面方式度量依赖性：I(X; Y) = 0 当且仅当 X 和 Y 为独立随机变量。从一个方向很容易看出：当 X 和 Y 独立时，p(x,y) = p(x) p(y)，因此：

特征筛选

from sklearn.feature_extraction.text import CountVectorizer

from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import mutual_info_classif


#选择K个最好的特征，返回选择特征后的数据
#arr = SelectKBest(mutual_info_classif, k=2).fit_transform(tfidf, target[:99])


from nltk.corpus import stopwords
import collections
import pandas as pd
import numpy as np
import os
import codecs

pos_list=[]

with open('../Sentiment_IMDB/aclImdb/train/pos_all.txt','r',encoding='utf8')as f:
    line=f.readlines()
    pos_list.extend(line)
neg_list=[]
with open('../Sentiment_IMDB/aclImdb/train/neg_all.txt','r',encoding='utf8')as f:
    line=f.readlines()
    neg_list.extend(line)
#创建标签
label=[1 for i in range(12500)]
label.extend([0 for i in range(12499)])
#评论内容整合
content=pos_list.extend(neg_list)
content=pos_list

stop_words=set(stopwords.words('english'))
count_vectorizer = CountVectorizer(stop_words=stop_words)
tfidf_transformer = TfidfTransformer()
tfidf = tfidf_transformer.fit_transform(count_vectorizer.fit_transform(content))
print (tfidf.shape)

arr = SelectKBest(mutual_info_classif, k=2).fit_transform(tfidf[:24999], label)
print(arr)

Task5

朴素贝叶斯原理

模型概述

朴素贝叶斯方法，是指
朴素：特征条件独立
贝叶斯：基于贝叶斯定理
根据贝叶斯定理，对一个分类问题，给定样本特征x，样本属于类别y的概率是
$$p(y|x)=\frac{p(x|y)p(y)}{p(x)}...........................(1)$$
在这里，x是一个特征向量，将设x维度为M。因为朴素的假设，即特征条件独立，根据全概率公式展开，公式（1）可以表达为
$$p(y=c_k|x)=\frac{{\prod }_{i=1}^{M}p(x^i|y=c_k)p(y=c_k)}{{\sum }_{k}p(y=c_k){\prod }_{i=1}^{M}p(x^i|y=c_k)}...........................(2)$$
这里，只要分别估计出，特征$x^i$在每一类的条件概率就可以了。类别y的先验概率可以通过训练集算出，同样通过训练集上的统计，可以得出对应每一类上的，条件独立的特征对应的条件概率向量。
如何统计，就是下一部分——学习——所关心的内容。

学习（参数估计）

下面介绍如何从数据中，学习得到朴素贝叶斯分类模型。概述分类方法，并提出一个值得注意的问题。

学习

经过上述步骤，我们就得到了模型的基本概率，也就完成了学习的任务。

分类

通过学到的概率，给定未分类新实例$X$，就可以通过上述概率进行计算，得到该实例属于各类的后验概率$p(y=c_k|X)$，因为对所有的类来说，公式（2）中分母的值都相同，所以只计算分子部分即可，具体步骤如下：

拉普拉斯平滑

到这里好像方法已经介绍完了，实则有一个小问题需要注意，在公式（3）（4）中，如果从样本中算出的概率值为0该怎么办呢？
下面介绍一种简单方法，给学习步骤中的两个概率计算公式，分子和分母都分别加上一个常数，就可以避免这个问题。更新过后的公式如下：

可以证明，改进以后的（7）（8）仍然是概率。平滑因子$\lambda =0$即为（3）（4）实现的最大似然估计，这时会出现在本节开始时提到的0概率问题；而$\lambda =1$则避免了0概率问题，这种方法被称为拉普拉斯平滑。

朴素贝叶斯应用场景

朴素贝叶斯常见应用场景

1文本分类/垃圾文本过滤/情感判别

这是应用最多的地方了，即使现在分类器层出不穷，在文本分类场景中，朴素贝叶斯依旧占据一席之地。在文本数据中，分布独立这个假设基本是成立的。而垃圾文本过滤和情感分析用朴素贝叶斯也通常能取得很好的效果。

2多分类实时预测

对于文本相关的多分类实时预测，被广泛应用，简单又高效。

3推荐系统

协同过滤是强相关性，但是泛化能力略弱，朴素贝叶斯和协同过滤一起，能增强推荐的覆盖度和效果。

朴素贝叶斯优缺点

大多数的分类算法，决策树,KNN,逻辑回归，支持向量机等都是判别方法，而朴素贝叶斯却是生成方法。

不仅如此，朴素贝叶斯很直观、计算量也不大。在很多领域有广泛的应用。

朴素贝叶斯的优点

1多分类问题

分类效率稳定，复杂度也不会有大程度上升。

2缺失数据处理

朴素贝叶斯算法能够处理缺失的数据。在算法的建模时和预测时数据的属性都是单独处理的。因此如果一个数据实例缺失了一个属性的数值，在建模时将被忽略，计算是否属于某类概率时也将被忽略。

3更少的数据

对小规模的数据表现很好，能个处理多分类任务，更进一步，它不会因小规模的样本而产生过拟合的数据。如果你没有太多的训练数据，请试试朴素贝叶斯算法。

朴素贝叶斯的缺点也很明显，对输入数据的表达形式很敏感。

朴素贝叶斯 sklearn 参数学习

这个太多了，没时间一个一个实践了，贴一个链接慢慢看。
https://blog.csdn.net/qq_36523839/article/details/81505841

利用朴素贝叶斯模型结合 Tf-idf 算法进行文本分类

https://blog.csdn.net/yyy430/article/details/88346920