吴恩达机器学习 EX8 第二部分 推荐系统 协同过滤
2、推荐系统
在第一部分练习,实现协同过滤学习算法,并将其应用于电影评级数据集。这个数据集由1到5的等级组成。数据集有nu = 943个用户,nm = 1682个电影
在第二部分练习中,计算协同适配目标函数和梯度。在实现了成本函数和梯度之后,学习用于协同过滤的参数
2.1 导入模块和数据
导入模块
import matplotlib.pyplot as plt
import numpy as np
import scipy.io as scio
import scipy.optimize as opt
import cofiCostFunction as ccf
import checkCostFunction as cf
import loadMovieList as lm
import normalizeRatings as nr
import imp
imp.reload(cf) # 重新加载模块
plt.ion()
导入数据
# ===================== Part 1: Loading movie ratings dataset =====================
data = scio.loadmat('ex8_movies.mat')
Y = data['Y'] # 1682 x 943 , containing ratings 1-5 of 1682 movies on 943 users
R = data['R'] # 1682 x 943 , where R[i, j] = 1 if and only if user j gave a rating to movie i
显示前两个电影用户的评价,评价为0的需要和R结合才知道用户是否对该电影做了评价
```python
Y[:2]
array([[5, 4, 0, ..., 5, 0, 0],
[3, 0, 0, ..., 0, 0, 5]], dtype=uint8)
显示前两个电影用户是否对电影做了评价
R[:2]
array([[1, 1, 0, ..., 1, 0, 0],
[1, 0, 0, ..., 0, 0, 1]], dtype=uint8)
显示所有电信已评价的平均分
# From the matrix, we can compute statistics like average rating.
print('Average ratings for movie 0(Toy Story): {:0.6f}/5'.format(np.mean(Y[0, np.where(R[0] == 1)])))
Average ratings for movie 0(Toy Story): 3.878319/5
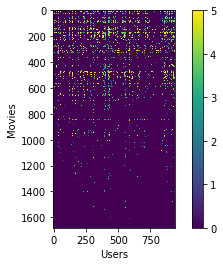
2.2 显示电影评价矩阵图
# We can visualize the ratings matrix by plotting it with plt.imshow
plt.figure()
plt.imshow(Y)
plt.colorbar()
plt.xlabel('Users')
plt.ylabel('Movies')
Text(0,0.5,'Movies')
2.3 协同过滤代价函数及梯度下降函数(cofiCostFunction.py)
2.3.1 导入数据
导入数据
# ===================== Part 2: Collaborative Filtering Cost function =====================
# Load pre-trained weights (X, theta, num_users, num_movies, num_features)
data = scio.loadmat('ex8_movieParams.mat')
X = data['X'] # 1682, 10
theta = data['Theta'] # 943, 10
num_users = data['num_users'] # 943 users
num_movies = data['num_movies'] # 1682 movies
num_features = data['num_features'] # 10
取几条测试数据,方便测试协同过滤代价函数算法
# Reduce the data set size so that this runs faster
num_users = 4
num_movies = 5
num_features = 3
X = X[0:num_movies, 0:num_features]
theta = theta[0:num_users, 0:num_features]
Y = Y[0:num_movies, 0:num_users]
R = R[0:num_movies, 0:num_users]
2.3.1 协同过滤代价函数及梯度下降函数
无正则化协同过滤代价函数公式:
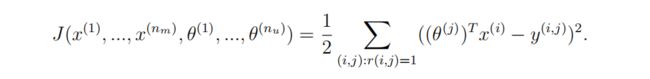
无正则化梯度下降公式,既要更新未评价电影可能评价以便推荐,又要更新用户的电影评价参数:
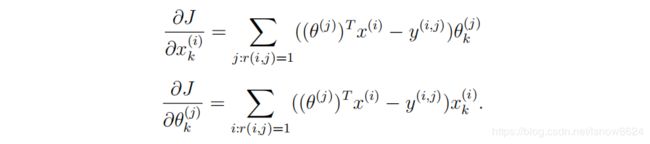
正则化代价函数公式:
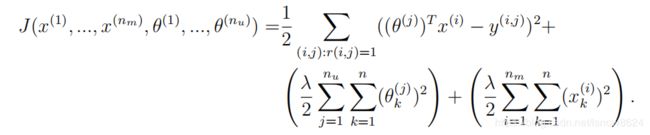
正则化梯度下降公式:
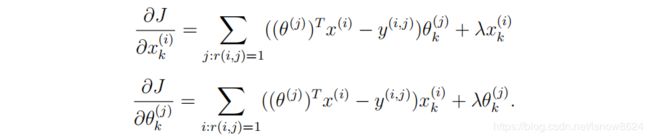
import numpy as np
def cofi_cost_function(params, Y, R, num_users, num_movies, num_features, lmd):
X = params[0:num_movies * num_features].reshape((num_movies, num_features))
theta = params[num_movies * num_features:].reshape((num_users, num_features))
# You need to set the following values correctly.
cost = 0
X_grad = np.zeros(X.shape)
theta_grad = np.zeros(theta.shape)
hypothesis = (np.dot(X, theta.T) - Y) * R # 假设函数
cost = np.sum(np.power(hypothesis, 2)) / 2 + lmd * np.sum(np.power(theta, 2)) / 2 + lmd * np.sum(np.power(X, 2)) / 2 # 代价函数
X_grad = np.sum(np.dot(hypothesis, theta)) + lmd * X
theta_grad = np.sum(np.dot(hypothesis.T, X)) + lmd * theta
# ==========================================================
grad = np.concatenate((X_grad.flatten(), theta_grad.flatten()))
return cost, grad
调用函数测试代价函数,OK
# Evaluate cost function
cost, grad = ccf.cofi_cost_function(np.concatenate((X.flatten(), theta.flatten())), Y, R, num_users, num_movies, num_features, 0)
print('Cost at loaded parameters: {:0.2f}\n(this value should be about 22.22)'.format(cost))
Cost at loaded parameters: 22.22
(this value should be about 22.22)
2.3.2 计算梯度函数
import numpy as np
def compute_numerial_gradient(cost_func, theta):
numgrad = np.zeros(theta.size)
perturb = np.zeros(theta.size)
e = 1e-4
for p in range(theta.size):
perturb[p] = e
loss1, grad1 = cost_func(theta - perturb)
loss2, grad2 = cost_func(theta + perturb)
numgrad[p] = (loss2 - loss1) / (2 * e)
perturb[p] = 0
return numgrad
2.3.3 梯度检查函数(checkCostFunction.py)
import numpy as np
import computeNumericalGradient as cng
import cofiCostFunction as ccf
def check_cost_function(lmd):
# Create small problem
x_t = np.random.rand(4, 3)
theta_t = np.random.rand(5, 3)
# Zap out most entries
Y = np.dot(x_t, theta_t.T) # 4x5
Y[np.random.rand(Y.shape[0], Y.shape[1]) > 0.5] = 0
R = np.zeros(Y.shape)
R[Y != 0] = 1
# Run Gradient Checking
x = np.random.randn(x_t.shape[0], x_t.shape[1])
theta = np.random.randn(theta_t.shape[0], theta_t.shape[1])
num_users = Y.shape[1] #5
num_movies = Y.shape[0] #4
num_features = theta_t.shape[1] #3
def cost_func(p):
return ccf.cofi_cost_function(p, Y, R, num_users, num_movies, num_features, lmd)
numgrad = cng.compute_numerial_gradient(cost_func, np.concatenate((x.flatten(), theta.flatten())))
cost, grad = ccf.cofi_cost_function(np.concatenate((x.flatten(), theta.flatten())), Y, R, num_users, num_movies, num_features, lmd)
print(np.c_[numgrad, grad])
print('The above two columns you get should be very similar.\n'
'(Left-Your Numerical Gradient, Right-Analytical Gradient')
diff = np.linalg.norm(numgrad - grad) / np.linalg.norm(numgrad + grad)
print('If you backpropagation implementation is correct, then\n'
'the relative difference will be small (less than 1e-9).\n'
'Relative Difference: {:0.3e}'.format(diff))
调用函数进行梯度检查
# Check gradients by running check_cost_function()
cf.check_cost_function(0)
[[-3.56295836 -6.96402424]
[-1.00563885 -6.96402424]
[-4.4682411 -6.96402424]
[-0.47329276 -6.96402424]
[ 0.93962486 -6.96402424]
[ 0.83719522 -6.96402424]
[-1.16465985 -6.96402424]
[-8.51743725 -6.96402424]
[ 7.97097947 -6.96402424]
[ 0.78489665 -6.96402424]
[-0.12752571 -6.96402424]
[ 1.82303345 -6.96402424]
[ 0.46414771 19.22131512]
[-2.80701519 19.22131512]
[ 0.58187894 19.22131512]
[ 3.6048716 19.22131512]
[ 2.5917378 19.22131512]
[ 3.27112377 19.22131512]
[ 0.89022317 19.22131512]
[ 7.54758452 19.22131512]
[-0.28430213 19.22131512]
[-1.05752892 19.22131512]
[ 0.22939012 19.22131512]
[-0.83047517 19.22131512]
[ 0.21545439 19.22131512]
[ 5.06782125 19.22131512]
[-0.26359675 19.22131512]]
The above two columns you get should be very similar.
(Left-Your Numerical Gradient, Right-Analytical Gradient
If you backpropagation implementation is correct, then
the relative difference will be small (less than 1e-9).
Relative Difference: 8.774e-01
2.3.4 正则化协同过滤代价函数
调用函数,显示正则化代价后损失值
# ===================== Part 4: Collaborative Filtering Cost Regularization =====================
# Evaluate cost function
cost, _ = ccf.cofi_cost_function(np.concatenate((X.flatten(), theta.flatten())), Y, R, num_users, num_movies, num_features, 1.5)
print('Cost at loaded parameters (lambda = 1.5): {:0.2f}\n'
'(this value should be about 31.34)'.format(cost))
Cost at loaded parameters (lambda = 1.5): 31.34
(this value should be about 31.34)
2.3.5 正则化协同过滤梯度检查
调用函数,显示正则化后的损失
# ===================== Part 5: Collaborative Filtering Gradient Regularization =====================
print('Checking Gradients (with regularization) ...')
# Check gradients by running check_cost_function
cf.check_cost_function(1.5)
Checking Gradients (with regularization) ...
[[ -4.36941112 -3.95684881]
[ -0.21871005 -3.65805218]
[ 5.77697894 -0.91201277]
[ -4.8644835 -3.62082946]
[ 4.32694342 -2.20704293]
[ 4.01271874 -1.4139862 ]
[ 3.48118842 -2.69106077]
[ -8.63024242 -4.09446365]
[ 2.4254279 -1.61498693]
[ -2.08842214 -4.56845536]
[ -0.84510525 -3.3875812 ]
[ -2.83680037 -5.28581432]
[ -2.21223772 -10.09433968]
[ 2.77180236 -7.64989317]
[ -5.7241062 -9.64544601]
[ 5.06154114 -6.35197803]
[ -0.92615819 -9.59880744]
[ -7.98956529 -10.27095382]
[ 1.36984379 -7.51082741]
[ -0.78536699 -9.56139494]
[ 1.10137301 -7.58284169]
[ 0.81715462 -9.209929 ]
[ 0.34545142 -8.57836758]
[ -3.63894407 -9.23192199]
[ -1.22785735 -9.60622813]
[ 5.92659558 -5.61293442]
[ -0.4687617 -8.78552714]]
The above two columns you get should be very similar.
(Left-Your Numerical Gradient, Right-Analytical Gradient
If you backpropagation implementation is correct, then
the relative difference will be small (less than 1e-9).
Relative Difference: 8.105e-01
2.4 为用户推荐电影
2.4.1 数据初始化
加载数据
# ===================== Part 6: Entering ratings for a new user =====================
movie_list = lm.load_movie_list()
显示前5部电影
movie_list[:5]
['Toy Story (1995)',
'GoldenEye (1995)',
'Four Rooms (1995)',
'Get Shorty (1995)',
'Copycat (1995)']
初始化推荐值为0
# Initialize my ratings
my_ratings = np.zeros(len(movie_list)) # 1682
更新基本电影的推荐值
# Check the file movie_ids.txt for id of each movie in our dataset
# For example, Toy Story (1995) has ID 0, so to rate it "4", you can set
my_ratings[0] = 4
# Or suppose did not enjoy Silence of the lambs (1991), you can set
my_ratings[97] = 2
# We have selected a few movies we liked / did not like and the ratings we
# gave are as follows:
my_ratings[6] = 3
my_ratings[11] = 5
my_ratings[53] = 4
my_ratings[63] = 5
my_ratings[65] = 3
my_ratings[68] = 5
my_ratings[182] = 4
my_ratings[225] = 5
my_ratings[354] = 5
print('New user ratings:\n')
for i in range(my_ratings.size):
if my_ratings[i] > 0:
print('Rated {} for {}'.format(my_ratings[i], movie_list[i]))
New user ratings:
Rated 4.0 for Toy Story (1995)
Rated 3.0 for Twelve Monkeys (1995)
Rated 5.0 for Usual Suspects, The (1995)
Rated 4.0 for Outbreak (1995)
Rated 5.0 for Shawshank Redemption, The (1994)
Rated 3.0 for While You Were Sleeping (1995)
Rated 5.0 for Forrest Gump (1994)
Rated 2.0 for Silence of the Lambs, The (1991)
Rated 4.0 for Alien (1979)
Rated 5.0 for Die Hard 2 (1990)
Rated 5.0 for Sphere (1998)
# ===================== Part 7: Learning Movie Ratings =====================
print('Training collaborative filtering ...\n'
'(this may take 1 ~ 2 minutes)')
# Load data
data = scio.loadmat('ex8_movies.mat')
Y = data['Y'] # 1682, 943
R = data['R'] # 1682, 943
Training collaborative filtering ...
(this may take 1 ~ 2 minutes)
# Y is a 1682x943 matrix, containing ratings (1-5) of 1682 movies by
# 943 users
#
# R is a 1682x943 matrix, where R[i,j] = 1 if and only if user j gave a
# rating to movie i
# Add our own ratings to the data matrix
Y = np.c_[my_ratings, Y] # 1682, 944
R = np.c_[(my_ratings != 0), R] # 1682, 944
2.4.2 数据均值归一化
首先需要对结果矩阵进行均值归一化处理,将每一个用户对某一部电影的评分减去所有用户对该电影评分的平均值
然后我们利用这个新的矩阵来训练算法。 如果我们要用新训练出的算法来预测评分,则需要将平均值重新加回去。我们的新模型会认为新用户给每部电影的评分都是该电影的平均分。
import numpy as np
def normalize_ratings(Y, R):
m, n = Y.shape
Ymean = np.zeros(m)
Ynorm = np.zeros(Y.shape)
for i in range(m):
idx = np.where(R[i] == 1)
Ymean[i] = np.mean(Y[i, idx])
Ynorm[i, idx] = Y[i, idx] - Ymean[i]
return Ynorm, Ymean
调用函数,将数据均值归一化
# Normalize Ratings
Ynorm, Ymean = nr.normalize_ratings(Y, R)
均值归一化后数据
Ynorm[:2]
array([[ 0.1214128 , 1.1214128 , 0.1214128 , ..., 1.1214128 ,
0. , 0. ],
[ 0. , -0.20610687, 0. , ..., 0. ,
0. , 1.79389313]])
平均值数据维度
Ymean.shape
(1682,)
# Useful values
num_users = Y.shape[1]
num_movies = Y.shape[0]
num_features = 10
推荐的电影及参数
# Set initial parameters (theta, X)
X = np.random.randn(num_movies, num_features)
theta = np.random.randn(num_users, num_features)
print('X.shape: ', X.shape, '\ntheta.shape: ', theta.shape)
X.shape: (1682, 10)
theta.shape: (944, 10)
initial_params = np.concatenate([X.flatten(), theta.flatten()])
lmd = 10
使用fmin_cg训练梯度
def cost_func(p):
return ccf.cofi_cost_function(p, Ynorm, R, num_users, num_movies, num_features, lmd)[0]
def grad_func(p):
return ccf.cofi_cost_function(p, Ynorm, R, num_users, num_movies, num_features, lmd)[1]
theta, *unused = opt.fmin_cg(cost_func, fprime=grad_func, x0=initial_params, maxiter=100, disp=False, full_output=True)
theta.shape
(26260,)
# Unfold the returned theta back into U and W
X = theta[0:num_movies * num_features].reshape((num_movies, num_features))
theta = theta[num_movies * num_features:].reshape((num_users, num_features))
print('Recommender system learning completed')
print(theta)
Recommender system learning completed
[[ 0.91699048 0.4821224 1.27262161 ... -0.43692712 1.52193012
1.01839969]
[-0.15461202 -0.01501969 0.36127297 ... -0.84198856 -0.38771395
-1.09592094]
[ 0.24856211 0.39626609 -0.1427684 ... 0.79426876 0.8323979
0.30108613]
...
[-1.32452211 1.75322313 -0.02867434 ... -1.34717043 0.63452904
-0.83119787]
[ 0.56969387 -0.01676459 0.83224533 ... 0.0987597 1.53914541
0.61056713]
[-1.0378453 0.62133146 -0.17118228 ... -1.70869891 0.75068908
-1.51608081]]
2.4.3 推荐电影
# ===================== Part 8: Recommendation for you ====================
p = np.dot(X, theta.T)
my_predictions = p[:, 0] + Ymean
indices = np.argsort(my_predictions)[::-1]
print('\nTop recommendations for you:')
for i in range(10):
j = indices[i]
print('Predicting rating {:0.1f} for movie {}'.format(my_predictions[j], movie_list[j]))
print('\nOriginal ratings provided:')
for i in range(my_ratings.size):
if my_ratings[i] > 0:
print('Rated {} for {}'.format(my_ratings[i], movie_list[i]))
Top recommendations for you:
Predicting rating 12.1 for movie Night of the Living Dead (1968)
Predicting rating 11.6 for movie Addams Family Values (1993)
Predicting rating 11.6 for movie Umbrellas of Cherbourg, The (Parapluies de Cherbourg, Les) (1964)
Predicting rating 11.4 for movie Grand Day Out, A (1992)
Predicting rating 11.2 for movie Love Is All There Is (1996)
Predicting rating 11.1 for movie African Queen, The (1951)
Predicting rating 11.0 for movie Mediterraneo (1991)
Predicting rating 10.9 for movie Hudsucker Proxy, The (1994)
Predicting rating 10.5 for movie Home Alone (1990)
Predicting rating 10.4 for movie Four Rooms (1995)
Original ratings provided:
Rated 4.0 for Toy Story (1995)
Rated 3.0 for Twelve Monkeys (1995)
Rated 5.0 for Usual Suspects, The (1995)
Rated 4.0 for Outbreak (1995)
Rated 5.0 for Shawshank Redemption, The (1994)
Rated 3.0 for While You Were Sleeping (1995)
Rated 5.0 for Forrest Gump (1994)
Rated 2.0 for Silence of the Lambs, The (1991)
Rated 4.0 for Alien (1979)
Rated 5.0 for Die Hard 2 (1990)
Rated 5.0 for Sphere (1998)
前一篇 吴恩达机器学习 EX8 第一部分 异常检测