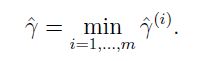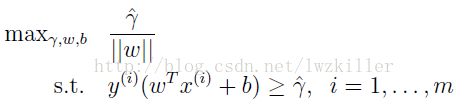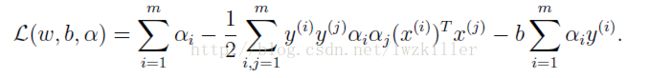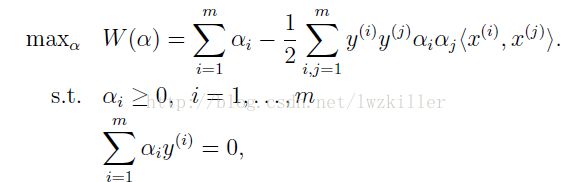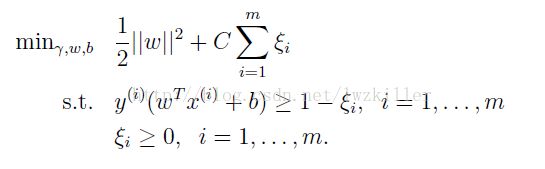支持向量机(Support Vector Machine)
关于支持向量机，这里只解释一些概念以及关于超平面参数是如何计算的，本篇不对参数优化推导过程进行详解，这块比较复杂，个人也需要时间捋一捋，日后再做整理。
首先，SVM的分类器为：
，其中令
为0时，即为该分类器的超平面，在二维中即是一条直线，如下图所示：
1.函数间隔
函数间隔表达式：
，当训练样本
，只要将该样本的输入与输出代入该公式，即可计算该训练样本的函数间隔。函数间隔仅仅反映该样本偏离超平面的程度，间隔越大，表明该点到超平面的距离就越大。这里以二维空间为例，直线ax+by+c=0，对于点(x0,y1)的函数间隔可以这样去理解，我们可以求出直线上横坐标为x0的纵坐标y0，那么函数间隔也即是b(y1-y0)这个数值的绝对值。这说明什么？对于任意一点，都可以计算以该点横坐标对应直线上的一个点，此时就可以比较这两个点纵坐标相差程度，如果相差越大，表明该点偏离直线程度较大，也即是该点到直线的距离越大，但这个间隔并不是该点到直线距离的真实值，它只是反映点到直线距离这层关系。对于N维情形也是如此，我们可以固定前面N-1维的坐标值，计算超平面最后一维所对应的数值，最后根据这两个点的最后一维的差值与该维系数的乘积作为函数间隔来反映该点到超平面的距离大小，当然固定哪些维数的坐标值，任由自己选择。
2.几何间隔
对于给定超平面
，如果我们同时对w，b进行缩放，肯定不会影响超平面所在的位置。那么我们对超平面的参数同时缩放
，也即向量w变为
，b变为
。通过这样变化，我们可以得到他的几何间隔(几何间隔也即是点到超平面的距离)：
如果
，我们会发现函数间隔与几何间隔相等。关于这种情况，大家可以简化维数，自己以二维直线为例验证下，找下实体感受。眼光犀利的兄弟，就不会去验证，因为他们知道上面的几何间隔公式就是我们所学的点到直线的距离公式。
3.优化转换
针对线性可分情况，我们知道对于最差样本，无论是函数间隔还是几何间隔，在训练样本中肯定都是最小的。优化最终目的就是最大化这些最差样本的最小间隔。我们可以获取最差样本的函数间隔：
我们同样可以获取最差样本的几何间隔：
进一步优化表达式：
考虑上面有限制条件w的模必须为1，我们可以将之去掉，又转换到函数间隔上来，得到优化表达式：
再看，因为我们对w、b任意缩放，都不会改变超平面的位置，所以这里可以缩放使最小函数间隔为1，那么优化表达式又转换成下面：
后面就是根据拉格朗日对偶条件以及KKT可优化极值条件(这块后续另起一篇详细说明)，进行求解了，进一步优化转换：
构造拉格朗日表达式：
优化后的结果最终转换为拉格朗日表达式进行极值求解各个参数。
4.超平面参数w、b计算
这里着重讲解下是如何求解超平面参数w、b
我们根据拉格朗日表达式对w和b进行偏导求解，得到如下表达式：
知道了w的形式，我们可以将w回代到拉格朗日表达式中，可得：
由于后面表达式为0，进一步简化为：
这里面只有afa是待求的参数，根据KKT条件的优化问题，我们可以优化下面表达式：
这种情形可以通过SMO(sequential minimal optimization)算法进行afa求解，再根据上面的afa与w的关系，可以解出向量w，关于b的求解，这里做以下解释：
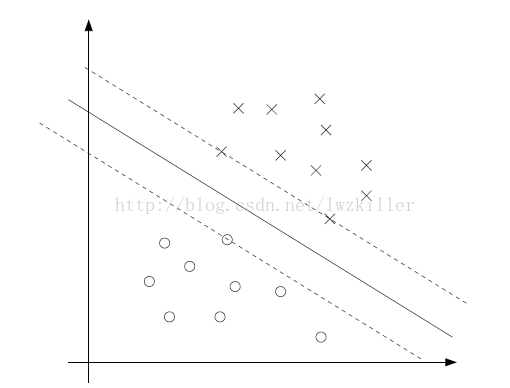
下图×是正样本，○为负样本
在正样本和负样本中各找一个最差样本，那么我们就可以计算出b。这里我们如何来判定正负样本中，哪个样本为最差样本？这是最关键的。 我们还是以二维为例，可以更直观的给予描述：直线ax+by+c=0，如果c不定，那么这条直线是不是可以平移经过每一个样本点？每经过一个样本点，就相当于该点在这直线上，那么我们是不是可以确定这条直线了？确定直线也就是确定c的值。c值反映直线在Y轴上的截距，但不是真的截距，相差一个系数。我们可以找到正样本的最小截距，以及负样本的最大截距，那么分割线的截距就是两截距的平均值。
5.核函数
核函数优点及性质：
【1】将低维线性不可分情形转换至高维线性可分；
【2】无需寻找低维映射到高维上的映射函数，一个核函数可以直接计算出结果，不需要高维映射函数映射成一高维向量，再计算高维向量之间的点积，节省大量运算时间；
【3】核矩阵的半正定性可以试图判别事先定义的函数是否是核函数，如果不满足，该函数就不是核函数
6.非线性可分
对于非线性可分情形，我们通常不会利用核函数将低维转换至高维情形进行处理，因为核函数这个东西本身就不好进行选定，我们也不知道选取的核函数是否真的就可以将线性不可分转换成线性可分。事实上，对于某些样本的干扰，我们通常使用软间隔进行分类：
对于线性可分，我们通常限制函数间隔是大于等于1的，但是对于不可分情形，有些样本的
值是可以大于1的，这样它的函数间隔就有可能小于0，这里允许个别样本的错分类发生，关于这部分的优化计算有空另起一篇加以说明。