图像特征— —Gabor特征
概念
Gabor变换属于加窗傅立叶变换,Gabor函数可以在频域不同尺度、不同方向上提取相关的特征。
Gabor小波与人类视觉系统中简单细胞的视觉刺激响应非常相似。它在提取目标的局部空间和频率域信息方面具有良好的特性。虽然Gabor小波本身并不能构成正交基,但在特定参数下可构成紧框架。Gabor小波对于图像的边缘敏感,能够提供良好的方向选择和尺度选择特性,而且对于光照变化不敏感,能够提供对光照变化良好的适应性。上述特点使Gabor小波被广泛应用于视觉信息理解。
与传统的傅立叶变换相比,Gabor小波变换具有良好的时频局部化特性。即非常容易地调整Gabor滤波器的方向、基频带宽及中心频率从而能够最好的兼顾信号在时空域和频域中的分辨能力;Gabor小波变换具有多分辨率特性即变焦能力。即采用多通道滤波技术,将一组具有不同时频域特性的Gabor小波应用于图像变换,每个通道都能够得到输入图像的某种局部特性,这样可以根据需要在不同粗细粒度上分析图像。此外,在特征提取方面,Gabor小波变换与其它方法相比:一方面其处理的数据量较少,能满足系统的实时性要求;另一方面,小波变换对光照变化不敏感,且能容忍一定程度的图像旋转和变形,当采用基于欧氏距离进行识别时,特征模式与待测特征不需要严格的对应,故能提高系统的鲁棒性。
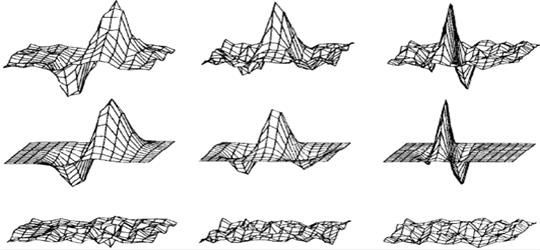
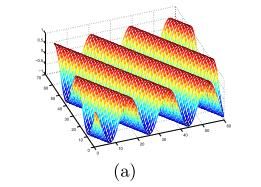
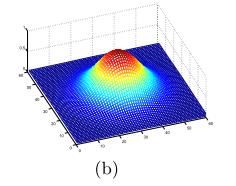
Gabor变换所采用的核(Kernels)与哺乳动物视觉皮层简单细胞2D感受野剖面(Profile)非常相似,具有优良的空间局部性和方向选择性,能够抓住图像局部区域内多个方向的空间频率(尺度)和局部性结构特征,如图所示。这样,Gabor分解可以看作一个对方向和尺度敏感的有方向性的显微镜。
同时,二维Gabor函数也类似于增强边缘以及峰、谷、脊轮廓等底层图像特征,这相当于增强了被认为是面部关键部件的眼睛、鼻子、嘴巴等信息,同时也增强了诸于黑痣、酒窝、伤疤等局部特征,从而使得在保留总体人脸信息的同时增强局部特性成为可能.它的小波特性说明了Gabor滤波结果是描述图像局部灰度分布的有力工具,因此,可以使用Gabor滤波来抽取图像的纹理信息。
然而,大部分基于Gabor特征的人脸识别算法中,只应用了Gabor幅值信息,而没有应用相位信息,主要原因是Gabor相位信息随着空间位置呈周期性变化,而幅值的变化相对平滑而稳定,幅值反映了图像的能量谱,Gabor幅值特征通常称为Gabor 能量特征(Gabor Energy Features)。
Gabor变换
Gabor变换的本质上还是对二维图像求卷积。二维卷积运算的效率就直接决定了Gabor变换的效率。
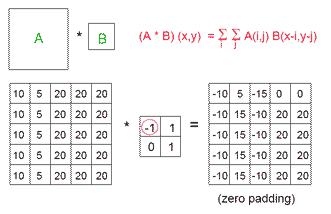
下图中,A是待处理的图像,B是Gabor变换的核函数。
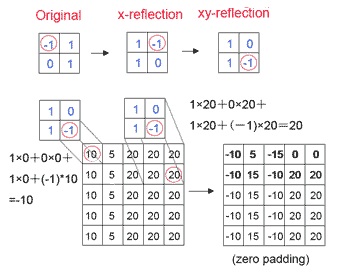
现在求A与B的卷积,我们首先对A的右边界和下边界填充0(zero padding),然后将B进行180度旋转(水平翻转后,再垂直翻转)。
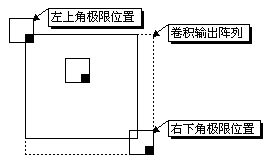
然后用B中的每个值依次乘以A中相对位置处的值并进行累加,结果填入相应位置处(注意红圈位置)。通常二维卷积的结果比A、B的尺寸要大,如下图所示。
Gabor函数
通过频率参数和高斯函数参数的选取,Gabor变换可以选取很多纹理特征,但是Gabor是非正交的,不同特征分量之间有冗余。 Gabor是有高斯核函数与复正弦函数调制而成,如下图所示。
图(a)为偏移x轴30°的正弦函数,图(b)为高斯核,图(c)为对应的Gabor filter。可以看出正弦函数是如何在空间上具有局部性的。
Gabor滤波器可以在多个尺度多个方向进行滤波,下面举个栗子。
Gabor滤波后的效果图(每行是同一尺度,每列是同一方向)
Gabor特征提取
先对图像I(x,y)进行实数形式的Gabor变换,得到处理后的图像。
举个栗子,我们需要处理的图像大小为128x128,可以先通过变换得到处理后的图像,大小也是128x128。直接提取特征的话,特征维数太高,不利于后续处理。一般对图像分块,分别水平和垂直方向取16等分,将整个图像分成64个16x16大小的子图像块,如下图所示。
然后计算每一块对应的能量。
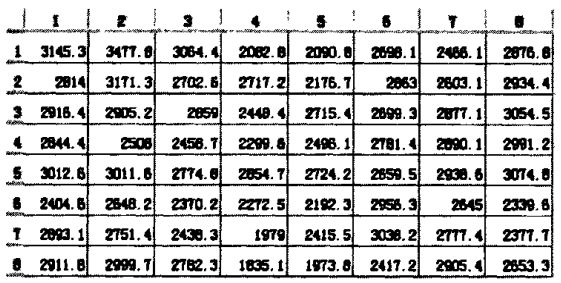
计算之后得到如下图所示的联合空间频率能量矩阵Energy。
最后将能量矩阵降维成1x64的行向量,作为原始图像在某一方向和尺度变换后的特征向量。